中2数学 五角形を三角形に変形させる方法

写真は、090224、中2数学の授業です。

今日、埼玉県はまた雪です～（積もるのかな？）。
昨日から、けっこうな寒さです。
普通の冬のようですが、花粉は相変わらず飛んでいるようで★

篠津中期末テスト、中2の数学は今日（090303）ですね。
1週間前に、昨年度の期末テストを勉強しています。
特に説明しておきたいものは、板書していますね。

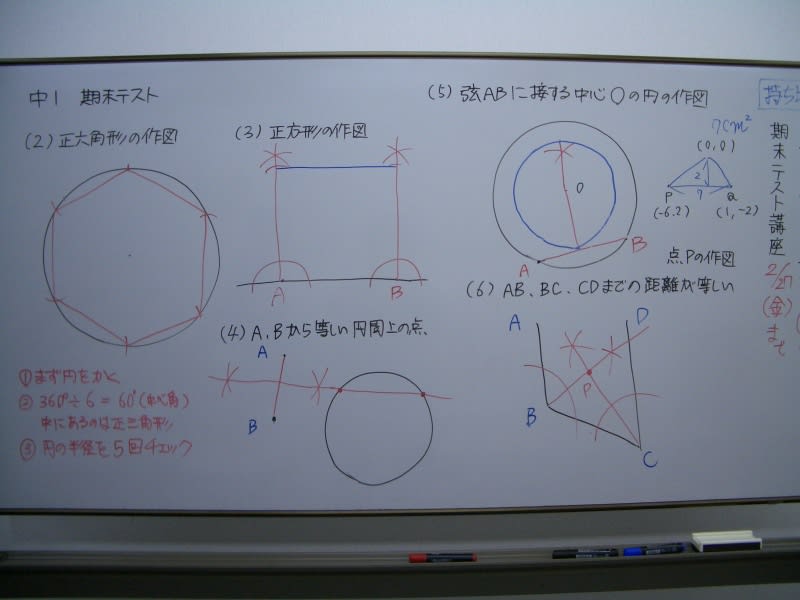
写真の左にあるのは「引き算の証明」です。
ぬるい穴埋めの証明ではなく、すべて記述するものです。
アビットのテキストP61の問59と同じ形の問題ですよ。

∠ADE＝90°－∠EDC
∠CDG＝90°－∠EDC
正方形の角度90°を使う証明でしたね。

写真の右上にあるのは、面積の等しい三角形を答える問題です。
「底辺と高さが等しい三角形は、面積も同じ」
この法則を使って、順々に見つけていきましょう。

写真の右下にあるのは、等積変形の問題です。
昨年度の過去問の中では、難しいと思います。

たとえば、四角形を三角形にするぐらいなら・・・。
アビットのテキスト「1本目」にも出ていてカンタンです。

ただ、昨年度の問題は、五角形を三角形にするものです。
つまり、2段階の変形が必要なのですね。
アビットのテキスト（プリント）「2本目」のレベルです。

2本目までできていないと、難しいかも★

そんなわけで、一気に変形させないで、順を追って変形させています。
まず、五角形ABCDEを四角形ABFEに変形。
そのあと、四角形ABFEを三角形ABPに変形させます。

基礎的な三角形の等積変形を2回やれば、完成しますよね。

この問題そのものをやったことがなくても・・・。
四角形を三角形に変形させることができれば、できる問題です。
あとは、知識の組み合わせ方でしょうね。

それこそが「応用力」というものでしょう。

さて、今日で期末テストが終わりなのですが・・・。
今度の日曜日（090308）は、休む間もなく北辰テストですね★
今日から新中2＆新中3は、北辰テスト過去問の勉強ですよ。

普段からしっかり取り組んでいれば、間際であわてないですみます。
テスト当日も大切ですが、もっと大切なのは普段からの「準備」です。
普段からの準備で、できる問題を増やしておきましょう☆

中1数学 期末テストはコンパスの作図

写真は、090225、中1の数学の授業です。

明日（090303）が、篠津中、中1の数学期末テストです。
今回の範囲は、「比例・反比例」と「平面図形」です。
昨年度と同じ試験範囲ですね。

ちなみに、比例の「点の移動する問題」ですが・・・。
昨年度には出題されていませんが、一昨年は出題されています。
少し難しいところですよね。

アビットの数学確認テスト、「1MJ-24」を見直しておいてください。

写真は、昨年度の3学期期末テストの問題を解説しています。
「平面図形」の内容であるコンパスの作図が、何問か出ていますね。
どれも、今までの勉強で描けるものばかりですよ。

それでも、1問だけ、あまりなじみのない図形が★
正方形を描けという問題です。
模範的な描き方は、以下のような感じです。

①横に長い線をかく（←これだけは、自由にかく）
②その線の垂線を2本、上に長めにコンパスで作図する
③横長の線と垂線、接したところをそれぞれA、Bとする
④ABの幅にコンパスを合わせる
⑤垂線1本目、Aにコンパスの針を刺し、ABの幅を垂線にチェック
⑥垂線2本目、Bにコンパスの針を刺し、ABの幅を垂線にチェック
⑦ラスト、チェックしたところを結ぶ

これで正方形を描けるのがわかりますか？
おそらく、他のやり方もあると思いますが。

中1のメンバーも、それなりに正方形は描けているのですが・・・。
線をかくときの作図で、コンパスを使っていない場合がありました。
自分の勘で、直線を引いているのですね。

数学は、理論や根拠を発揮するところがありますよね。
極力「勘だけ」は避けましょう。
「それって、なぜ直角と言えるの？」とツッコミが入らないように★

垂直な直線をかくにも・・・。
「コンパスでこう作図したから直線だ」というように。
コンパスで作図した跡を残しておくのが鉄則ですよ。

090227の新聞で21年度「埼玉県公立高校入試問題」を見ましたか？
数学では、毎年必ず1問、コンパスを使った作図の問題が出ます。
21年度のコンパス問題は、「∠PAB＝30°」の作図でした。

中1のみなさんは、アビットでも最近勉強しましたよね。
60°、45°、75°、さらには135°の角度も作図できるでしょう♪
平成19年度の入試問題と同じものも、最近勉強したばかりです。

高校入試問題といっても、中1からの勉強が大切ですよ☆

↑数学期末テストの得点、期待しています。

中2数学 足し算＆引き算の証明

写真は、081021、中2数学の授業です。

090302＆090303は、篠津中の期末テストですね。
この内容は、090214の土曜復習講座で、復習しました。
なかなか難しいところですよね★

ちなみに、昨年度の期末テストには、アビット使用テキストから・・・。
「引き算の証明」の記述問題が出題されています。
写真は「問60」なのですが、「問59」が出題されましたよ。

写真右の「引き算の証明」を見てみましょう。

テキストには、引き算の部分が・・・。

∠ABD＝90°－∠BAD
∠CAE＝180°－90°－∠BAD
　　　　　＝90°－∠BAD

・・・こんな感じで書かれています。

初めての勉強の場合は、説明がザックリしすぎですね★
それぞれの角度、∠ABDと∠CAEは同じ引き算で表せます。
だから、「∠ABD＝∠CAE」と説明できるわけですね。

でも、難しいところはここです。
「90°って、どこのこと？　こっちは180°って、どこ？」
ある程度できる人でも、このような質問がありますね。

だから、アビット新白岡校の板書では、以下のように書きます。

△ABDより
∠ABD＝180°（△ABDの内角の合計）－90°－∠BAD
　　　　　＝90°－∠BAD

一直線の180°より
∠CAE＝180°－90°（△ABCの90°）－∠BAD
　　　　　＝90°－∠BAD

同じ引き算なので、「∠ABD＝∠CAE」ということです。

2つの三角形の合同条件は・・・。
「直角三角形の斜辺と1鋭角がそれぞれ等しい」です。

え？　まだ難しいって？　そうなんです～。
やはり、図を目の前にしてライブで教えてもらわないと★
指差しながら「ここから、コレとコレを引いてるんだよ」と。

ところで、この問題ができると、トクすることがありました。
現中3と集団指導にて、平成18年度入試問題を勉強していたときです。
教科は数学で、大きい「2」の（3）の問題です。

写真と同じような図形ですが、「合同な図形」ではありません。
解説には、三平方の定理で解くように書いてあります。
解説だけだと少し複雑ですが、説明すればわかりやすくなります。

私が「これって、計算が複雑だよね～」と言っていると・・・。
ある中3は、やたらとカンタンな計算にて短時間で解いていました。
私は「すごいな～、そういえば中2の『引き算の証明』か！」と。

この「引き算の証明」をマスターしていると、カンタンでした。
ああ、やっぱり勉強しておくものだなあと。
新中3には、カンタンな解き方で教えたいと思います。

でも、この「足し算と引き算の証明」が身についていないと・・・。
せっかくのカンタンな解き方も、理解できません★
日々、身につけるべきものは身につけて進んでいきましょう☆