中3理科 埼玉県公立高校入試問題 運動とエネルギー

写真は、120204、中3入試対策の授業です。

土曜日ですが、急遽、中3公立高校入試対策の授業を入れました。
「これ、たぶん解説読んでも難しいかな～」
そんな問題を、集団指導で解説しています。

埼玉県公立高校入試の過去問は、一度はガチで解いてもらいます。
マル・バツと点数は、こちらでつけますが・・・。
間違え直しは、宿題にすることが多いですね。

家でじっくりゆっくり、解答・解説を確認して直してください。
主に数学で、解説を読んでも難しい問題はあるでしょう。
そのときは、ぜひ質問してくださいね。

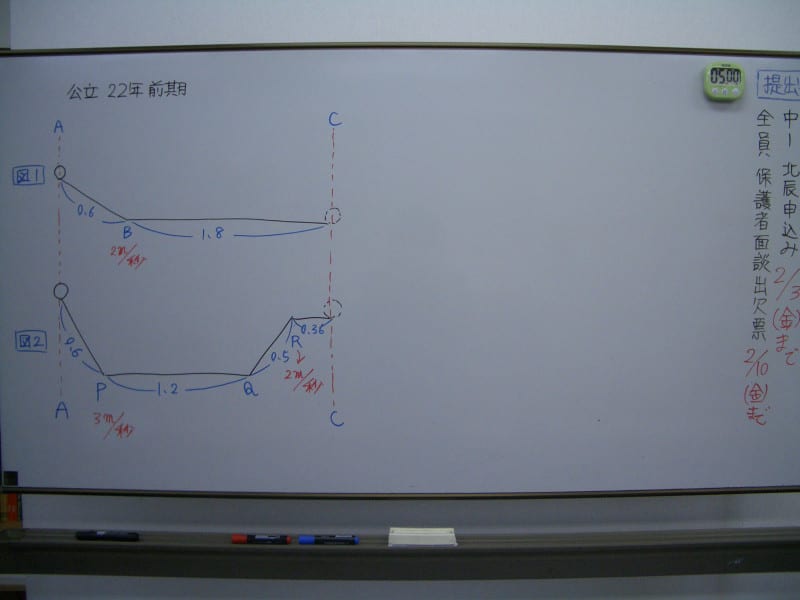
さて、写真は平成22年度、前期入試の問題です。
わかっている情報は、すでに全て書き込んであります。

問題「斜面の角度や経路を変えて小球の速さを調べる実権をしました。図1と図2があります。スタートのAからゴールのCまで、どちらが早く着くでしょうか」

ただし、「図1」「図2」「同じ」の三択問題ではありませんよ。
その理由を、記述（文章や箇条書き）で書いていく問題なのです。
解答用紙のスペースは、けっこう広く取られています。

教室のある子どもは、なんとなく「図1かな～」と言っていましたが。
さて、どうなるでしょうか？
しっかり計算しながら、見ていきましょう。

すべて、「速さ・時間・距離」の計算で説明できます。
「距離÷速さ＝時間」を使いますよ。
ただし、ある区間の「平均の速さ」が求められるかどうか？

◆ 図1

AB間は、ずっと2m／秒で転がっているわけではありません。
だんだん速くなって、B地点で最速の2m／秒なのです。
さて、AB間斜面の「平均の速さ」は？

Aでの速さ　0m／秒
Bでの速さ　2m／秒
AB間の平均の速さ　（0＋2）÷2＝1（m／秒）

AB間の時間　0.6÷1＝0.6（秒）

BC間の時間　1.8÷2＝0.9（秒）

ラスト、AC間の時間　0.6＋0.9＝1.5（秒）

図1のかかる時間は、「1.5秒」になりました。

◆ 図2

AP間は、ずっと3m／秒で転がっているわけではありません。
だんだん速くなって、P地点で最速の3m／秒なのです。
さて、AP間斜面の「平均の速さ」は？

Aでの速さ　0m／秒
Pでの速さ　3m／秒
AP間の平均の速さ　（0＋3）÷2＝1.5（m／秒）

AP間の時間　0.6÷1.5＝0.4（秒）

PQ間の時間　1.2÷3＝0.4（秒）

同じように、QR間の「平均の速さ」を求めましょう。

Qの速さ　3m／秒
Rの速さ　2m／秒
QR間の平均の速さ　（3＋2）÷2＝2.5（m／秒）

QR間の時間　0.5÷2.5＝0.2（秒）

RC間の時間　0.36÷2＝0.18（秒）

ラスト、AC間の時間　0.4＋0.4＋0.2＋0.18＝1.18（秒）

図2のかかる時間は、「1.18秒」になりました。

だから、図2のほうが早くCに着くのですね。
先ほどの子どもの予想は、外れてしまいました★

↑できましたか？

上のやり方を、ほぼそのまま書いても正解だと思います。
ただ、解説には、もう少しアッサリした書き方がありました。
ただし、それだけ見ても果たしてこの問題を理解できるのか・・・？

ベタに「は・じ・き」の計算をしていけば、時間は出ます。
これが一番わかりやすいかなあと思って、説明しました。

埼玉県公立高校入試は、考え方を説明する問題が出題されますよね。
単なる暗記では書けないこともあるでしょう。
普段から「過程」「プロセス」を重視して、勉強していきたいですね☆

---------------------------------------------------------------------

　公式ホームページはこちらです！