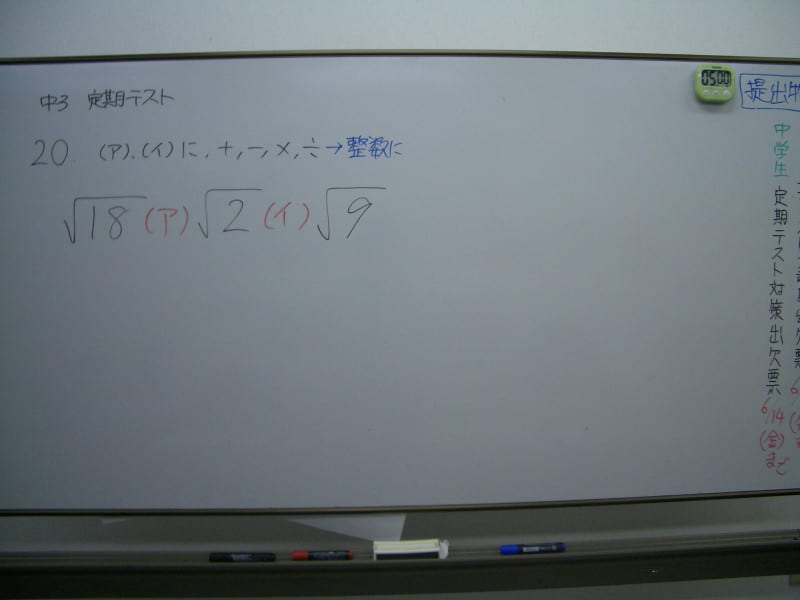中3数学 篠津中定期テスト対策、確率と√の組み合わせ

写真は、130613、中3数学の授業です。

篠津中の第1回定期テストが、130617＆130618ですね。
過去問を使って、定期テスト対策の授業をしていますよ。
写真にある問題のみ、少し考える問題でしたね。

その問題を見てみましょう。

問題「次の（ア）、（イ）に、＋、－、×、÷の記号を入れて計算します。同じ記号は2回使わないこととします。このとき計算の結果が整数になるようにするためには、（ア）、（イ）に入れる記号の組み合わせは、全部で何通りありますか」

問題の式は、「√18（ア）√2（イ）√9」です。

答えが整数になるパターン、1種類だけ見つけるだけなら・・・。
何かしら、テキトーに記号を入れていけば正解しそうですが。
「全部で」何通りですからね★

テキトーにではなく、下準備が必要になると思います。

「何通り」というと、確率を思い出しますよね。
今回のテスト範囲は、中2の確率と中3の平方根の最初まで。
ちょうど、この2つを組み合わせると解けますよ♪

まず、「＋、－、×、÷」を2つ使う確率の表を作りました。
これで、使う記号が何通りあるのかがわかります。
樹形図をかいて、「4×3＝12」でもわかりますよ。

次に、問題の式を簡単にしておきましょう。
「√18（ア）√2（イ）√9」→「3√2（ア）√2（イ）－3」
これで、記号を入れても計算しやすくなりましたよ。

下準備ができれば、あとは12通りの計算をしていくだけ。
「12通りもやるの？」と思うかもしれませんが・・・。
写真の通り、すぐにできる計算ばかりです。

整数になるのは、「7通り」となります。

↑12通りの計算は、写真をクリックして確認してくださいね。

単純な知識から計算して終わりの問題だけでなく・・・。
色々な知識を組み合わせて、問題が解けるといいですよね。
それでこそ、「応用問題、発展問題が解けた」ことになります☆

----------------------------------------------------------------------

　公式ホームページはこちらです！