(2)「候補数を消去する」手筋
⑧で手筋「Jelly Fish」と「Squirmbag」に付いて書きました。凄く難しいと感じた事と思います。そのときは軽く読み流して下さい。
実は「超難問」と言っても出版社によりそのレベルはまちまちです。あまり難しい手筋が登場しなくても「超難問」との文言が入った問題集もあります。色々な問題を解いてきた経験上、大雑把に言って「Sword Fish」と,次回のブログから登場する「3国同盟」「4国同盟」、更に先で書きます「上級ステップ」の手筋の幾つかをマスターすれば多くの「超難問」は解決出来ると考えています。
そこで、この「Sword Fish」に習熟することが、実践的に重要な戦略かと考え、2題ほど例題を載せます。この2題の問題解決に取り込む過程で、どうすれば見落とす事無く「Sword Fish」等を発見出来るかを、研究して頂きたいと思います。(マーちゃん推薦はオセロ石を用いる方法です)
例題4を図1に例題5を図2に掲げました。図3が例題4の解答で、図4が例題5の解答です。
図1
例題4 図1で「Sword Fish」を見出してください。(その先の作業は問いません)
図2
例題5 図2で「X-wing」または「Sword Fish」の成立のマスの配置を指摘してください(問題は”指摘”までです)
(以下に例題4と例題5の解答を載せます)
図3
解答(例題4)は上図の黄色マスの配置です。候補数7について3列の配置で「Sword Fish」成立です(今後b2、b8、e5、e8、h5、h8の候補数7が消去出来ます)
図4
解答(例題5) 図4で黄色マスの配置が「Sword Fish」の配置です。(候補数3の3列の配置で成立し、今後c7、e1、e9、g7で候補数3が消去出来ます)
次回ブログは「3国同盟」についてです。
(2)「候補数を消去する」手筋
⑧「Jelly Fish」と「Squirmbag」を考察する。
「X-wing」を2次元の「Sword Fish」を3次元の手筋と見なせば、それを拡張して4次元が「Jerry Fish」であり、5次元が「Squirmbag」です。図1に「Jerry Fish」の様子を、図2に「Squirmbag」の様子を示します。
図1を見てください。
図1
図1の様に
『ある候補数Xについて、候補数Xが4個(最低2個でも可)存在する行が4行あり、その4行に登場する候補数が4列にわたるとき、その4列については、他のマスには候補数Xは存在しない。言い換えれば候補数Xを消去出来る』
これが手筋「Jelly Fish」の内容です。行と列を入れ替えても成立します。図1で言えば、ある候補数XがA~Pの様に存在する場合、黄色マスにXは存在しません。言い方を変えれば、黄色マスから候補数Xを消去出来ます。
(図1では、便宜上A~P以外の候補数は省略されているとします.。又各行で候補数の存在は2~4個でも可)
図2は手筋「Squirmbag」の様子を示しますが、説明は「Jelly Fish」とほぼ同じですから省略します。
図2
さて例題3です。お考え下さい。
例題3 図3はある数独の問題を解いていったところ、(2)⑥の「Sword Fish」まで調べつくしたが、局面に何らの変更も現れず、行き止った状態とします。「オセロ石」を用いての作業で「Jelly Fish」又は「Squirmbag」の成立を発見してください。(超難問です。ヒントを読むのが”やぶさか”で無い方はヒントを元にお考え下さい。ヒント・・・候補数1を列について考察すると「Suirmbag」が発見できます)
図3
解答 図4は候補数1について、1が確定しているマスには白を置き、候補数1の存在するマスには黒を置いています。この状態で「Jelly Fish」又は「Squirmbag」の成立を考察するわけです。

図4
既に「Jelly Fish」について調べたが、成立を見出せず、又行について「Squirmbag」について調べたが、その成立を確認出来ず、考察を列にシフトしている状態とします。
8列の内、全部が候補数が5個以下の列です、そこで丁寧に調べ尽くしいくとなると、「順列・組合せ」の知識で8個の中から5個選ぶ組合せ数=8個の中から3個選ぶ組合せ数= (8×7×6)÷(3×2×1)=56 となり、56の場合全てを調べ尽くすにしては絶望的に多い数です。
そこでマーちゃんはこの様な場合、次の様に物事を進めます。候補数2の列をベースに出来ないか?今の場合、6列と8列の候補数が2個です。この2つの列に登場する行はf、g、h行。
ではそのf、g、h行のみを含む列は無いか?この3個の行のみを含む列は無いが、プラス1個多い行は1列と9列。とすると1列と9列を加えた4つの列はどの行に渡るのか調べると{c、d、f、g、h}行。もう1列に加わって貰わなくてはなりません。{c、d、f、g、h}行に収まる列は無いか、祈るような気持ちで確かめると5列がその条件を満たしています!「Squirmbag」成立です。図5でその様子を示します。
図5
黄色マスの配置が全体として「Squirmbag」です。
そこで{c、d、f、g、h}行から、黄色マス以外のマスの候補数1のある黒石を除きます。取り除いた石のマスの候補数1を消しゴムで消去して図6に至ります。
図6
候補数1では新たな発見が無いので、図6から、黒石を元に戻し図7となります。
図7
今後は候補数2~9までオセロ石を用いての考察を進めます。ただ新たな変化が見出せなければ(1)から(2)の考察をくり返すことになる訳ですが、これは大変時間が掛かります。そこで取り除いた1の影響のある事柄に絞って、今までに考察してきた点を再度調べ直すのがベストかと、マーちゃんは考えます。
(2)候補数を消す手筋
⑦「オセロ石」を用いる
手筋というより手筋を見出す方法論です。候補数の書かれた例えば図1から「X-wing」や「Sword Fish」をより確実に見つけたいと思います。ここでマーちゃんは「オセロ石」を用います。オセロゲームに使用される白面と黒面を持つ石です。最初は碁石を使用していましたが、オセロ石の方が碁石より小さいくて安定性が良いので、今はオセロ石を使用しています。手に入りづらければ碁石でも良いでしょう。
それではどう使用するのか。図1を見て下さい。
図1
この問題は前回のブログで使用した問題で、この局面で「X-wing」や「Sword Fish」を捜しました。この局面でオセロ石をどう用いるのか。前提が一つあります。市販の「数独」や「ナンプレ」問題をいきなり解くのではなく、予めオセロ石を入れることの出来る大きさの問題用紙を用意して欲しいのです。面倒と感じられることでしょうが、多くて9個の候補数を書き入れる為にも、オセロ石を用いて「Sword Fish」等の手筋をより視覚的に見つける為にも、一度はやや大きめの用紙を作成し、以後はコピーして使用する事をお勧めします。図2を見てください。
図2
図2は候補数1について考えています。既に1が確定しているマスには白を置き、候補数1のあるマスには黒を置きます。そしてじっくりと石の配置を眺めます。最初は行について眺めます。まず「X-wing」が成立していないか、見ます。行について2個の候補数がその成立要件でしたから、2個の候補数のあるa行とh行を見ると、なんと最初から「X-wing」の成立が視覚的に発見できるではありませんか!
もし発見できなければ、次に列について考察し、それでも発見できなければ「Sword Fish」はどうかと考察を進めます。候補数1が終われば、候補数2について同じ様に考察を進め、最後は9まで進めます。
今は候補数1の段階で「X-wing」だけが発見されたとします。手筋「X-wing」により図3の様に、d9、f8、f9の黒を取り除き、かつ候補数1を消します。
図3
図3から更に黒を取り除き図4に至ります。
図4
さて候補数2から9まで、ご自分でやってみて下さい。
どの段階でこのような用紙にオセロ石を乗せて考察を始めるのがベストか?一概には言えませんが、今のところは”X-WingやSword Fishを見つけねばならない局面に達したとき」からと述べておきます。
さてマーちゃんは候補数3で「Sword Fish」を見つけました。図5見てください。
図5
この局面で、実は列について「X-wing」が成立しているのですが、それには気が付かなかったとの前提で話を進めます。「Sword Fish」が成立しないかを調べる為、行で候補数が3個または2個の行を考えます(候補数1個は考えると言うより、その1個の候補数のマスはその候補数が確定数となります)
この局面で該当行はa行、c行、f行、h行です。この4つの行から旨く3つの行を見つけて、その3行の候補数が3列に収まるか、考える訳です。見つけ出すには訓練と熟練が必要ですが、高校時代に習った数学の「順列・組合せ」を持ち出すまでもなく、4通り全てを丁寧に調べ尽くしてもいいわけです。
a行・f行・h行の3つの行は1列・3列・9列だけに候補数が存在しますから、「Sword fish」成立です。これらの列から他の候補数3の上の黒石を取り除き候補数3を消しゴムで消し、図6に至ります。
実は「X-wing」が成立しているのですが、と書きました。手筋「X-wing」で候補数を取り除いても、「Sword Fish」を用いたのと同様に図6に至ります。
図6
更に黒石を戻し、図7に至ります。
図7
その後は列について考察し、更には候補数4~9まで考える、というかオセロ石を用いての作業を続けるわけです。
この様な方法はもはや「数独解決」では無い、とお考えでしたら、オセロ石を用いないで、候補数を眺めることに集中してください。マーちゃんはこの方法は許されると考え愛用し、比較的簡単に、視覚的に、手筋を発見しています。次回のブログでは「X-wing」の更なる拡張(4次元)を紹介します。
(2)候補数を消去する手筋
⑦「Sword Fish」を捜す
X-wingが2行(あるいは2列)について成立した手筋ですから、この手筋を拡張しようと考えるのは自然の成り行きです。「Sword Fish」とは次の内容の手筋です。(いわば2次元から3次元への拡張です)。図1をご覧下さい、
図1
図1で、ある数(=Xと書く)の候補数の配置が(例えば)a行、f行、h行の3つの行に存在し、その3個の行に候補数Xが3個存在し、かつその3個が全て同じ列に存在する場合(水色ライン以外にある数Xは省略している)には、黄色マスにはある数Xは存在しない。言い方を変えれば黄色マスから候補数Xを消去できる、と言うものでした。(この表現は行を中心に記述していますが、行と列を入れ替えても、「Sword Fish」は成立します)
この事は証明も難しくありません。簡単に紹介します。例えば図1でマスAの値がXとすると(A=Xと記述)マスB.・C・D・Gから候補数Xは消去され、1列の黄色マスからもXは消去される。残ったマスE・F・H・IはX-wingとなるので3列と9列の黄色マスからもXは消去される。すなわち図1の全ての黄色マスからXは消去される。ここの証明が、もし分からない様でしたら読み飛ばしてください。
このことは図2のように3つの行が全て3個の候補数を持たなくても成立です。
図2
これ以外にも成立する場合はいろいろあります。そこで「Sword Fish」を正確に述べると
3つの行に候補数が3個または2個あり、登場した全ての候補数が3つの列に存在する場合、これら3つの列にその候補数は他には存在しない(行と列は入れ替えても良い)
となります。問題はこの「Sword Fish」をどうやって見抜くかです。暫く、例題2を考えて下さい。 
図3
例題2 上図3で、どんな候補数について、何処に「Sword Fish」が成立するでしょうか。又その効果として候補数を消去しなさい。
又同じ候補数で「X-wing」をも見抜いてください。解答は図4以下です。
図4
解答 図4の候補数3の黄色マスの配置が「Sword Fish」です。
その結果図5の水色のマスから3が消去されます。
図5
そして図6に至ります。「X-wing」は候補数3について、c2、i2、cc7、i7の4マスで成立し、同じく図6に至ります。
図6
さて、最も重要な事は、この「Sword Fish」をどうやって見抜くかです。このハードルを越えなければ「超難問」が解けないのでありば、どのようにしても見抜かなければなりません。「必ず見抜く」事は難しそうに見えます。でもご安心下さい。視覚化した上で「見抜く」方法があります。次回ブログではその方法を紹介し、更に難しいとされる「Jelly Fish」や「Squirmbag」を見つけることにも挑戦!です。
(2)候補数を消す手筋
⑥「X-wing」を捜す
さて、いよいよ「X-wing」です。数独の解法についての説明を読んだ事があれば、一度はこの「X-wing」の説明に接した事があると思いますが、改めて「X-wing」に述べます。下図1をご覧下さい。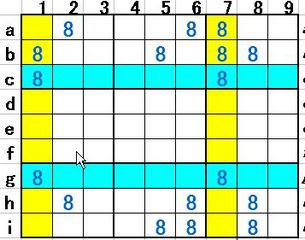
図1
図1は候補数8の配置を記録したものです。その特徴はc行とg行(水色のライン)には候補数8が2個だけ登場しています。しかもc行の8もg行の8も、共に1列と7列に存在しています。
この時、1列上と8列上(黄色のマス)には8は存在し得ない、言い方を変えれば、8を消去出来るのでした。その結果図2の局面に変化します。
図2
その理由を図3で説明します。
図3
今ある候補数(例えば8)の配置が図3の如くであったとします。詳しく書くと、候補数8はc行のマスAとBに存在し、かつg行のマスCとDに存在していて、青いライン以外では8を省略していいます。
この時 仮にA=8 ならば B≠8であり、その結果
かつC≠8 だから D=8
逆にA≠8 ならば B=8であり、その結果
D≠8 だから C=8です。
つづめて言えば『AとDが8』または『BとCが8』が成立しています。どちらが成立してもc行・g行・1列・7列にはA・B・C・Dマス以外に8は存在しえません。c行とg行には候補数は2個と言う前提でしたから、ここ以外に8は存在しないのは当然として、1列と8列に8は存在しないと言う新たな事実が現れ、その結果として黄色マスに存在する8は消されます。
この『AとD』並びに『CとD』を線分で結ぶと文字『X』の様になる事から「X-wing」と呼んだのだと思います。
ただ注意する点はA・B・C・Dの4マスが共に同一のブロックに属するときは「X-wing」の手筋は使えないと言うことです。
「X-wing」の理屈はそれほど難しいものではありませんが、問題を解く実戦の場で「X-wing」を見出すのはそれほど容易いではありません。
例題1で考えて下さい。問題はこの局面で「X-wing」を見出し、消去すべき数があれば消去しなさい、です。
例題1 ある数独の問題を解いていって、手筋を使い次の局面 に達しました。さて「X-wing」は何処にあるでしょうか?
解答 下の図の黄色いマスの候補数3が「X-wing」です。i2とi6(ピンクの数3)が消去されます。
3を消去して下の図に至ります。









