来年小学校に入学する孫の為の算数(足し算)プログラムが完成し、ママのやよいちゃんにファイルを送信した。
どんなプログラムかを語るには「公文式算数」を引き合いにするのが好都合だ。もし「公文式」をご存じでない方は以下の文で想像してほしい。(私は公文式教室で教えたことはないが、中学時代の同級生が教室を開催していたことがあり、時折数学に関して相談を受け、教室での様子を聞くことも何度かあった)
①公文式教室の教室生は席に着くと、先生から前回の学習の次の段階のプリントを渡される。
②教室生は渡されたプリントの問題を解いて、正解か否か先生に見てもらう。
③先生は渡されたプリントの解答が正解ならば赤丸を付け、不正解ならば何も付けない。
④答案を返された教室生は〇が付いていない問題を再考し、再度先生に渡す。全問が正解になるまで繰り返す。
⑤全問が正解になると、新しいプリントが教室生に渡される。
⑥一斉の授業は行われず、①～⑤が繰り返される。
私はエクセルを用いて足し算プログラムを作成した。右図がパソコン上の最初の画面で、公文式①に相当する。
孫(に限らずこのプログラムで学習する生徒・児童)は青い空欄に解答を入力し、右図のように正解だと『正しい〇』が、不正解だと『もういちど』はそのままで変化しない。ここは公文式の②と③に相当する。多分ママは『もういちど』の問題を再考するように孫に話してあるので、孫はもう一度問題を考えることになる。(公文式では④に相当)
さてここからがこの足し算プログラムの“みそ”だが、このプログラムにはマクロが組まれており、一定のキー操作をすることによって一瞬(1秒くらい)に、今までの画面は一新され、孫の前には新たな問題が現れる(右図 公文式では⑤と⑥に相当)。
プログラムにはより程度の高い問題も組み込まれていて、孫がその希望をママに伝えれば、更に高いレベルに移行できるようになっている。先生の役割をパソコンが代わりにやってくれるのだ。
さて孫の反応はどうだか？やよいちゃんからのメールによると実際にこのプログラムをやってみた孫の反応は「イマイチでした」とあった。要するに興味を示さなかったのだ。親などから出題されて、全問正解ならば「良く出来ましたね」と声をかけて貰うほうが楽しいらしい。人と会話を交わしながらの学習の方が面白いらしい。私のプログラムは小学校入学前の子どもには適さなかった様だ。
このプログラムは足し算プログラムだが、引き算・九九・掛け算などにも変更可能なので、孫が小学校低学年になった暁に改めて試してもらおうと思っているのだが・・・。
最近、『数学、それは宇宙の言葉』という、数学のエッセイ集を読み始めた。冒頭には「どの話もすてきなアイディアと鮮やかな結果で輝いている」と紹介され、50人の数学者が50の話を語っている。第1話が『神秘の数6174』で、ここに書かれた事実を私は初めて知ったのだが、引き算さえ出来れば小学生でも理解可能で、電卓さえあれば多くの人が体験できる事なので、ここで紹介してみたい。
まず4桁の数で同じ数字だけで表されないものを選ぶ(つまり、1111,2222,・・・9999以外の数を選ぶ)。それから、その4つの数字を並べ直して最大の数と最小の数を作る。それから、最大の数から最小の数を引くという演算をすると新しい数が得られる。新しい数が得られる度にこの演算を繰り返す。
具体的に説明しよう。
例えば、今年の西暦年数2022を選べば、この2、0、2，2から作られる最大の4桁数は2220で、最小数は0222。引き算をすると、2220−0222＝1998。
今度はこの1998から出発し、最大数9981−最小数1899＝8082。以下同様に、
8082から出発し8820−0188＝8352
8352から出発し8532−2358＝6174
6174から出発し7641−1467＝6174
ここまで来ると、これ以降、何度演算を続けても6174 が繰り返し現れることになる。この繰り返し現れる数を核と呼ぶことにする。
他の数で、もう少し見栄え良くやってみる。
1938から始めてみると
9831−1389＝8442 → 8442−2448＝5994
→ 9954−4599＝5355 → 5553−3555＝1998
→ 9981−1899＝8082 → 8820−0288＝8532
→ 8532−2358＝6174 これも、7回の演算で6174に達した。
このブログを読まれている方もやってみてほしい。実はどんな4桁の数からスタートしても6174 に到達するらしいのだ。この演算は1949年にインドの数学者D.R.カプレラが考案し、今ではカプレラの演算と呼ばれている。
ほとんどの4桁の数がこの特定数6174に達するのは何故かと、その理由が考えられ、その証明を通して、どんな4桁の数から出発しても、6174という唯一の核に到達することが明らかにされた。(ここではその証明は省略する)
実に簡単な演算の結果が面白い、6174を神秘の数と見るかは判断の分かれるところだが、魅力的な結果には違いない。 数学者の思考は２桁、3桁、5桁・・・に向かった。その結果を簡単に記しておくと、
2桁、5桁、7桁の数では核は現れない。
3桁の数では核は495
6桁の数では核は549945 と631764 となる。
さて私の思考は何回の演算をすれば6174に達するかに向かった。それを調べるにはエクセルの演算に頼るのが素早いと考えプログラムを組んだ。その結果1000～9998までの8991個の全ての4桁の数が最大7回の演算で6147に達することが確認出来た。（以下がエクセルによる計算結果。赤字の8991は7回目の演算結果6174が8991個あることを示している。それは1111,2222,3333,・・・,8888,9999を除く全ての4桁の数に等しい。）
昨年の今頃のブログに「見覚えのある図形だった」と題して文京区立昭和小学校の授業に触れた。そのブログの最後は「図形を手書きで描いたのだが見栄えの良いものにはならなかった。一工夫が必要と思っている」と書き終えていた。工夫の最終結論はプリント作成ソフト「Studyaid」を購入することだった。
数学の問題に関連して、数式や図形をプリントに印刷しようとする多くの教員などは「Word」以外ならば、数研出版のソフト「Studyaid」を使用していることだろう。私も25年ほど前からこのソフトを利用して試験問題や授業用プリントを作成していた。非常に便利で有難いソフトだった。ところが現役時代に使用していたパソコンを「Surface」に買い替えた段階で、そこに「Studyaid」をインストールしなかった。出来なかったとも言える。芝浦工業高校の講師を最後に数学を教えることが無くなり、特にこのソフトを利用しなければならない場面は消えていた。
ところが種々の事情からこのソフトが必要になって来ていた。ただ、値段は2万円以上するので足踏みをしてしまった。コロナ禍となって友と一献傾ける機会が減ったのは大変残念だったが、反面財布の中身は少し豊かになったのだ。そこで昨年このソフトを購入しパソコンにインストールした。
最近は特に、マーティン・ガードナー著などのパズル問題を解き始め、数時間考えることも多くなっている。その問題が解けた時などにはその解法を記述しておけば良いのだと気が付いた。
このソフトを上手く用いれば、ブログで数学の面白い問題を紹介することも出来ることに思い至り、このソフトの再使用に気合を入れて取り組み始めた。今後時折数学の問題やパズルを取り上げてみたい。
とういう訳で、今回のブログではマーティン・ガードナー著『数学ゲームⅡ』に載っていた問題を紹介したい。パズルを解くのがお好きな方は挑戦してみて下さい。初めて接する、面白い問題だった。
「先日、妻と私はあるパーティーに出席した。そのパーティーには他に4組の夫婦が出席し、参加者は丁度10人だった。そこそこで挨拶の握手が交わされたが、自分自身と握手をしたものはいないし、自分の配偶者と握手したものもいなかった。
さて握手がすっかり終わったとき、私は妻も含めて他の全ての9人に、幾人の手を握ったかと尋ねてみた。驚いたことに、それぞれは皆違った答えをしたのである。では私の妻は何人の方と握手をしたのだろうか？」
解答は「Studyaid」を用いて、来週の金曜日に。
追記 「Studyaid」では下図のようなプリントを作成出来た。
1ヶ月ほど前の1月16日(土)、妻が集めていたベルマークを近所の昭和小学校に持参したところ、現在は受付中止ということで、ビックリすると同時にガッカリした。しかし、箱の右上に貼られた「昭和小だより」(写真:右)に書かれてあった3つの図を見て、私の何かが強く反応した。見たことのある図だなと思いながら「昭和小だより」の全文を読んだ。
「素敵な話をお伝えしたい」として校長先生の授業参観の様子が書かれていた。
2年生の算数は分数の習い始めで、折り紙を折って4分1の大きさを作る学習をしていた。多くの子供は右図1のように折っていた。(対角線が折れ線となるような折り方)
中に一人右図２のように変わった折り方をしている子供がいた。図１のようにぴったり紙を折らないでずらして折っていた。校長先生が「ぴったり折るんじゃないの」と聞くと、わざわざずらして折っているという。その紙を広げた時に校長先生は驚いた。その折り目を見ると、4分1の大きさが出来ていた。
一度職員室に戻った後、どうしてその様な方法を思いついたのかを聞くために再度教室に行き、何故その方法を考えたのか担任に聞くと、「昨日、2分の1を作るときに右図3のような方法ができたからだと思います」と。その方法を考えた子供は図3の発想が基になり、それを柔軟に活用して図2が出来上がったと校長先生は気が付いた。
「だより」を立ち読みしている途中で、私はある図形を思いだしていた。1969年から13年間、都立向丘高校に勤務していた頃、授業で、私の趣味だったパズルを出しては生徒ともども楽しんだ。そのパズルの1題に次の様な問題があった。
「右図4の十字形にもう一本の線を引き、十字形を同じ形をした4つの図形に分けた後切り抜き、それを寄せ集めて正方形にしなさい」。少し難しいパズルだが正解に達する生徒も何人かいた。ここでは、ご自分で正解を考えようとする方の為にスペースを開け、正解は10行ほど下に書くと。
正解図。右の図(5図)の様に、もう一本の線を書くと、4つの同じ図形(合同な図形)に分かれている。この線に沿って鋏を入れ4つの部分に分けたのち、
組み合わせると図６のように正方形になる。この図形が「だより」の図2に似ていたのだ。
ここまでこのブログに付き合ってくださった方がいたら、ご苦労様でした。
追記１ ここまで書いてきたことを、昭和小学校の校長先生宛に、文を整えて封書で郵送したところ、今月に入って返信を頂いた。「そちら様からの手紙を、算数の授業を担任に伝えました。担任も学校だよりのことをすでに子供らに伝えて、一緒に喜びあっていたので、手紙のことを知らされたことで、さらに喜んでいました」とあった。
更に「・・・私も、教員になって以来、算数一本で研修を重ねてまいりました。それだけに、地域の方と算数・数学のことでお話が出来たことは、この上ない喜びです」とあり、私も嬉しかった。
追記2 ここから先はその後考えたこと。高校生に出題したパズルを逆にすると別のパズルになる、と気が付いた。
問題「図7の正方形に1本の線が書かれている。①もう一本の線を書き込み、正方形を4つの同じ図形に分けなさい。
②更にそれを切り抜いて寄せ集め十字形を作りなさい」。(正解は図6の様に線を加え、切り抜いて図5の様にする。「昭和小だより」図3より少し難しくなっているが本質的には同じ問題で、最終結果が十字形に到達するのが面白い)
追記3 教員現役のころは教材作成プログラム「Studyaid」を使用し、図形も含めプリントを作成していた。退職し、パソコンを買い替え「Studyaid」はインストールされていない。そこで図形を手書きで描いたのだが見栄えの良いものにはならなかった。一工夫が必要と思っている。
最近読み出した和算についての一冊に『江戸の数学教科書』(著:桜井進 出版:集英社)がある。第1章で江戸時代に和算がフィーバーした様子が語られ、第2章で円周率を求めようと奮闘した和算家たちの挑戦の様子が語られている。その中で「バーゼル問題」が紹介されていた。
「バーゼル問題」など初めて目にする御仁も多いことと思う。数学アレルギーの方には見たくもない数式が登場するかも知れないが、ここで私が紹介したいこと、えっ！ということが4つほどあり、それをご覧頂きたいので最後までお付き合い願えればと思う。
えっ！(1) 「バーゼル問題」とは右に掲げてある“自然数の平方の逆数の和”の値を求めよという問題で、式の後半に「・・・」とあるのは、無限に足すという意味だ。スイスの数学者ヤコブ・ベルヌーイはその値が確定することを証明したが、値を求めることは意外に難問で、解答を得られずに1705年に死去してしまった。ベルヌーイが暮らしていたスイスの都市バーゼルの名から「バーゼル問題」と呼ばれ、多くの数学者がその値を求めようとしてきた。
この問題を解決したのがオイラーで1735年のことだった。右がその最終解答で、その式をご覧いただこう。左辺に登場するのは自然数だけなのにその無限個の和の結果の右辺にΠ(円周率パイ)という超越数という数が登場する意外性。オイラー自身がその結果に驚いたと伝えられている。これがえっ！(1)だ。
えっ! (2)実はこの問題、オイラーの発見より13年前の1722年に和算家建部賢弘が解決していた。彼は、和算を知らない人でも聞いたことのある関孝和の高弟の一人。色々な業績があるが、円周率を小数点以下41桁まで算出していたことでも知られている。ヨーロッパ先んじて江戸中期の享保年間に日本で解決されていた。えっ！(2)だ。
えっ！(3)時代は一挙に現代に飛ぶ。「バーゼル問題」の証明はいろいろあり、この語で検索すると証明が現れる。今回は高校数学の範囲内での証明を読んだ。更にはYou Tube上でも証明は現れる。白板を用い講師が熱心に証明している。この方法だと、理解しづらい箇所では画面を一時stopし、熟慮しながら証明を読むことも可能だ。You Tube上での証明は今風だ。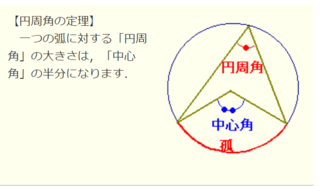
えっ！(4)You Tubeでの証明をいろいろ見ていたら、「中学数学の範囲内での証明法」が現れた。三平方の定理(ピタゴラスの定理とも呼ばれる)と円周角の定理(円周角は中心角の半分という定理)のみで証明していた。無限に加えることは中学校では学ばないのでこれだけは中学数学のレベルを超えているが、それ以外は基本的には中学数学の範囲内での証明だった。2002年にある数学者が証明したそうだが、この証明には心底驚いた。興味のある方はYouTube上で“中学数学でバーゼル問題”で検索を。