構造計算偽装問題[はなやか]なりし頃、私の世代では聞きなれない「耐震スリット」なる言葉がTVで語られていた(あるいは私の勉強不足?)。いわく「耐震スリットを設けていないから設計ミスだ・・・」云々。
どうやら鉄筋コンクリート造(以下RCと書く)の建物で、「構造耐力を持たせるRCの部分」と「耐力を持たないRCの部分」とが接する場合、両者の間にスリットを設ける、ということで、多くの建築関係者が、[律儀に]これを守っているらしい。
建築の仕事は、昔から(少なくとも第二次大戦後このかた)、「理科系」と言われ、そのためには、数学と理科ができることが必要、とされてきた。そして、ある頃からは、度が過ぎて、理数系だけを必死に勉強し、他の分野について学ぶことをおろそかにする傾向が生じている。特に、今30代から40代の方々に、その傾向が顕著のように私には思える。
さて、理科系が得意なはずの人たちが、なぜ先の《耐震スリットの必要性の理屈》を[律儀に]守ってしまうのか。
ほんとに理科系が得意なら、《耐震スリットの理屈》に疑問を呈して当然ではないだろうか。
《耐震スリットの理屈》には、大きく二つの疑問がある。
その一。構造物を、「外力に応じる部分」と「外力に応じない部分(言い方を変えれば《お荷物》になる部分)」とに分けるのは、ご都合主義も度が過ぎる。それとも、外力は、人が[勝手に決めた]通りに働いてくれるのか?
これは、木造建物の《耐力壁》:筋かいなど:を設けるという[考え方]に共通する。
その二。構造物をつくるときに、なぜ、わざわざ《お荷物》にしかならない箇所:dead lordにしかならない部分:をつくるのか。
構造物をつくるとき、特にRCのような重い材料を使うとき、つくられるすべての部分:形が、できるだけ外力に対して有効に働くように考えるのが『常識』ではないか。
昨日「マイヤールの仕事」を紹介したのは、彼が、本当の意味で「理科系」の人物であったこと、ものごとを理詰めで考える人だったこと、を知って欲しかったからでもある。彼のRC造には、無駄がない。すべての部分が意味がある。しかも美しい。
『理』とは「すじみち」のこと、「ものごとをすじみちを通して考えること」が「理科」であり「科学」のはずだ。それは決して、数学や物理の問題が解ける、計算がうまくできる、ということではない。単に計算ができても、それは「理科」「科学」を習得できていることではない。
残念ながら、最近のいわゆる「理科系の人」は、計算はできても「理詰めで考える」のが不得手のようだ。
「木造住宅耐震診断士」という「資格」がある。先日、その資格を得た幾人かと話をする機会があった。当然「木造」を理解しているものと思った。しかし違った。理解しているのは、木造建築にかかわる法律だった。「木造に関する法律の理解≠木造の理解」なのは自明ではないか。《法律の規定を充たせば耐震建物になる》と、ほんとに思っているのだろうか。恐ろしい話だ。
私には、「理科系の人」ほど、理科系ではないように見える。
なぜこんな事態になってしまったのか?
それは、次の機会に。
どうやら鉄筋コンクリート造(以下RCと書く)の建物で、「構造耐力を持たせるRCの部分」と「耐力を持たないRCの部分」とが接する場合、両者の間にスリットを設ける、ということで、多くの建築関係者が、[律儀に]これを守っているらしい。
建築の仕事は、昔から(少なくとも第二次大戦後このかた)、「理科系」と言われ、そのためには、数学と理科ができることが必要、とされてきた。そして、ある頃からは、度が過ぎて、理数系だけを必死に勉強し、他の分野について学ぶことをおろそかにする傾向が生じている。特に、今30代から40代の方々に、その傾向が顕著のように私には思える。
さて、理科系が得意なはずの人たちが、なぜ先の《耐震スリットの必要性の理屈》を[律儀に]守ってしまうのか。
ほんとに理科系が得意なら、《耐震スリットの理屈》に疑問を呈して当然ではないだろうか。
《耐震スリットの理屈》には、大きく二つの疑問がある。
その一。構造物を、「外力に応じる部分」と「外力に応じない部分(言い方を変えれば《お荷物》になる部分)」とに分けるのは、ご都合主義も度が過ぎる。それとも、外力は、人が[勝手に決めた]通りに働いてくれるのか?
これは、木造建物の《耐力壁》:筋かいなど:を設けるという[考え方]に共通する。
その二。構造物をつくるときに、なぜ、わざわざ《お荷物》にしかならない箇所:dead lordにしかならない部分:をつくるのか。
構造物をつくるとき、特にRCのような重い材料を使うとき、つくられるすべての部分:形が、できるだけ外力に対して有効に働くように考えるのが『常識』ではないか。
昨日「マイヤールの仕事」を紹介したのは、彼が、本当の意味で「理科系」の人物であったこと、ものごとを理詰めで考える人だったこと、を知って欲しかったからでもある。彼のRC造には、無駄がない。すべての部分が意味がある。しかも美しい。
『理』とは「すじみち」のこと、「ものごとをすじみちを通して考えること」が「理科」であり「科学」のはずだ。それは決して、数学や物理の問題が解ける、計算がうまくできる、ということではない。単に計算ができても、それは「理科」「科学」を習得できていることではない。
残念ながら、最近のいわゆる「理科系の人」は、計算はできても「理詰めで考える」のが不得手のようだ。
「木造住宅耐震診断士」という「資格」がある。先日、その資格を得た幾人かと話をする機会があった。当然「木造」を理解しているものと思った。しかし違った。理解しているのは、木造建築にかかわる法律だった。「木造に関する法律の理解≠木造の理解」なのは自明ではないか。《法律の規定を充たせば耐震建物になる》と、ほんとに思っているのだろうか。恐ろしい話だ。
私には、「理科系の人」ほど、理科系ではないように見える。
なぜこんな事態になってしまったのか?
それは、次の機会に。










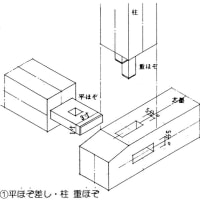
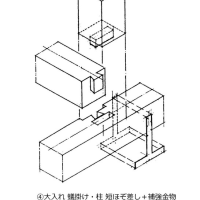






建物において、①局部的観点からは柱を短柱にさせないため、②外力をどの部材に分担させるかさせないかといった部分的且つ恣意的な話ではなく、建物の部材配置のバランスをよくするため、つまりいかにして建物を偏心させないか、この2点からです。(以下くどくどと書いている箇所についてはご容赦ください。)
まず短柱について。実務につきたてのころ、というかついてすぐ、スリットなるものの存在を知りました。
意匠主専攻卒だった当時のはな垂れが、その存在について知るはずもなく、早速先輩にこれなるものが何故必要なのかと問いました。先輩曰く「短柱にしないためだ」と。短柱とは何かとここで細々と書く必要はないと思いますが、話を進める上で一応確認のため書かせていただきます。柱の場合、支点間距離は階高となります。この間で柱は応力に対し変形しながら対応することになります。しかし垂れ壁や腰壁が柱に取り付く場合、柱は節点でそれらにより拘束され、自由に変形できる範囲はそれらの内々間へと狭くなってしまいます。これが所謂「短柱」と言われる状態でしょう。では何故この状態がいけないのか?先輩曰く「このような箇所で柱がせん断破壊してしまうからだ」との答え。同じ応力でも、支点間距離が短くなったために変形性能が小さくなってしまったら、せん断破壊を起こす(可能性がある)との説明。この理屈は、変形出来にくくなるのだから靱性が損なわれる分,脆弱になるのだろうなと素直に納得できます。これが局部的理由。
次に建物全体にかかわる理由。建物の剛心と重心がずれている、つまり偏心しているとき、水平力が加わると剛心を中心に建物が回転しようとする。荷重は重心にかかっているのでこの理屈も違和感はありません。回転が生じてしまうと、余分な曲げ・せん断力が発生して負担になりそうだというのも予想がつきます。マンションの梁間方向の壁は普通下から最上階まで耐震壁ですが、この梁間方向の壁に三方スリットを設けているのを見かけることが普通に多々あります。短柱でもないのに何故と不思議に思っていましたが、建物に偏心を起こさせないためだと教わりました。1階で10スパン程度で途中の階からセットバックしはじめて、最上階では5スパン程度になっているマンションをよく見かけますが、あのような形状だとちょうどセットパックが始まる通り心あたりが応力がきつくなるそうです。偏心を回避するためにまず行う方法は、セットバックしていな方の壁厚を上げていく。それでもだめな場合、セットバックしている方(重心から遠い方)の壁から順にスリットを切っていくのだそうです(無闇に切ってる訳でもなく、切り方にも順番がある)。そうすると剛心と重心が徐々に近づく(これも言われて見れば納得できます)。また実際面から言えば、法令なのでこれを満たさないと設計出来ない
(したことにならないとみなされる)との理由も勿論あると思います。「外力が人間の決めたように都合よく働いてくれるのか?」との問いかけがありましたが、上に述べたスリットを設ける理由はどちらも、外力を人間の都合のいい様に流せないものか、コントロール出来ないものかとの思いの結果だと感じます。
以上二つの理由をかきましたが、後者は(現状の計算法や仮定が妥当だとして)そのまま受け取りれるとしても、何故前者はだめなのでしょうか?せん断破壊とはそこまで忌み嫌うべきものなのでしょうか?結論はやはり「YES」。兎に角危険だから避けなければいけない。せん断破壊=脆性破壊、つまりRCで言えばコンクリートが飛び散り鉄筋がむき出しの状態になる事だと理解しています。そうなればどうか?鉄筋だけで圧縮応力(その他)に耐えなければなりませんが、当然鉄筋にそれを期待することは出来ません。後は最悪倒壊まで進むことになります。そうさせない建前の考え方が現在の曲げ降伏後の塑性域の耐力に期待した設計法。地震エネルギーを塑性変形までさせて吸収しようとする目論見。ヘルメットが有事の際に受けた衝撃で、自らを破壊することによりエネルギーを変換吸収し、頭を守るのと同じ理屈だと理解しています。倒壊はしないが塑性変形なので荷重がなくなった後も変形が残りますが、人命は守られるとの方針。納得できます。
ただそこまでせん断せん断と口うるさく言う割には、RCであれSRCであれ打ち継が必ず発生するので、そこでは必ずコンクリートはせん断している。これはどうなの??と昔から疑問でした。ソフトは無視しているようですね。それを言い出すと計算自体が成り立たないから。実際は打ち継面には上部からの支圧がかかっていますし、表面つるつるではないですし、壁筋なども効いてますから、ある程度のせん断耐力はあるのでしょう。現に建物もってますから。
======================================
スリットを設けたときのメリットと、設けなかったときにもしかしたら起こるかもしれない危険のデメリットを比べれば、前者が勝る気がします。
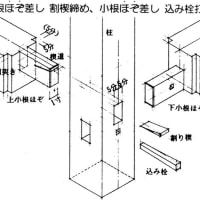
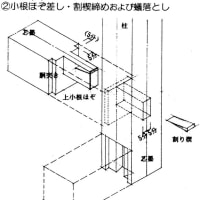
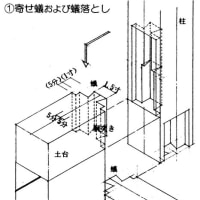
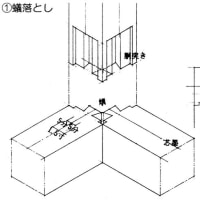
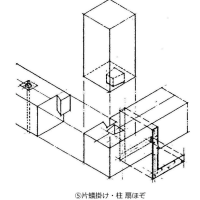
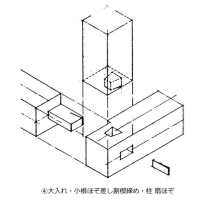
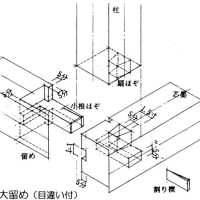
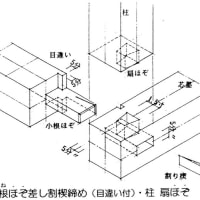
確か木造建築で「背割り」という技があると思います。「起こりうると予想される不都合にたいして、予め術を施す」という意味で言えば、スリットはこれと同じではないかと思います。はな垂れが話を伺った構造担当の方も、「スリット切らないに越したことはない」と言っていたのを付け加えておきます。ならば意匠設計者としては、安易にスリットに頼らない空間・架構を当初から計画すべきということか・・・しかしそれはものによるしな・・・難しいですね。
なぜならば、その人たちなら、いわゆる《短柱》になってしまうようなことは最初からやらないだろうし(そうなることが分かっていながら腰壁をつくる訳がない・・)、バランスがくずれるようなこともやらないでしょう。
まだ《○○学》がない時代の彼らは(ワット然り)、『自分の感覚』でものをつくるからです。ものをつくるために、一発で本質を見抜く力を、彼らは自ら養い、培っていたのだと思います。
ときどき、《たくさんの情報・知識(それも部分的な)》に煩わされない彼らは幸せだったなあ、と思います。
『自分の感覚』と、 『自分以外の感覚』にズレがある場合、どのように折り合いをつけられるのですか?
ものごとの本質(本質って何だ?)に迫っているかどうか、を考える、これは昔の人のあたりまえの考え方だったと思います。
「バランスよい平面計画がよい」これは自明です。ですが実際の設計活動においてこれに当てはまらない
場面が多々でてきます。例えば前に出ましたセットバックする集合住宅。「土地を有効活用するため制限一杯の容積を確保すべき」との社会的要求の前に、構造的に合理的だからとの理由で、「セットバックさせない範囲の高さで計画しましょう」と設計者が意見を言ったところで、通る話ではありません。一方で法規には、建物はバランスよくせよと謳っています(技術的理想もまた同じでしょう)。両者は懸絶している。設計者が取るべき道は二つ。何とかして両者を近づけ収めて行くか、「意に沿わないことはしたくない」とその仕事を降りるか・・・。
仮に設計するとなると、前に述べたように、短柱をつくらない・偏心を出来るだけ抑える、の2つの課題に直面します。(桁方向に)短柱を作りたくないしスリットも設けたくないとなれば、フレーム打設後、CBあるいはLGSなどで壁を作るしかない。前者は工費の面で、後者は居住性の面で現実的でない。となると、雑壁にスリットを設けて作るしかない。偏心を抑えるには、以前のように梁間方向の壁にスリットを設けていくしかない(もしこれ以外に方法があるのなら教えてください)。ただしここで注意しなければならない
ことは、法規なり指針なり告示なりで、スリットを設けなさいとか、設けましょうなどとは一言も書かれていない事です。(はな垂れが知る範囲では)。つまり法規を決めた人も、スリットを設けること自体が(本当は)よろしくないと知っていたのではないでしょうか。あるいは偏心率・剛性率などの基準を作っては見たものの、ここまでの事態が生じる事を想定していなかったか?・・・・・これは全くの想像でしかないですが。しかしいったいスリットは、いつごろ誰によって考え出されたものなのでしょうか。
スリットを設けて偏心を抑える作業などは、なるほど計算書上の辻褄合わせでしかなく、技術の本質的なことからかけ離れた事かも知れません。しかし、はな垂れはスリットについて、「理想・基準」と「現実」と
の「折り合いをつける」ための便利で有効な「方便」ではないかと思います。
なんの後ろ盾もなく市井で活動する我々は、技術者として「本質」を考え貫く事だけでは、生きていけないのもまた事実です。
はな垂れが構造や現行の計算法について学ばねばと考えたきっかけは、基準の中にある「31m」との数字が気になったからです。それはそれは半端な数字で、なぜ「30m」ではだめなのか、「1m」の違いにどれほどの意味があるのかに興味を持ったからです。いざ調べてみれば、この数字に科学的裏づけなどなく決まったものであり、見直されることもなく惰性でそのまま残っただけという事があっけなく分かってしまう。その後、この「31m」の約束事の理由を幾人かの構造担当に聞いてみたものの、誰もが「知らない・疑問に思ったことすらない」との答えに唖然。一番秀逸(劣悪だった)答えは「構造家はいちいちそんなもの気にしない。31が30になれば、それに合わせて計算するだけ。」これではもう「設計」ではなく、数字の帳尻だけをあわす「(事務)作業」でしかない。こんな計算の段取りだけ知っているだけの奴等に、デカイ面させる訳にいかないとの思いからです。
「古代人のように考える・・・いまいちぴんとこないな」と思いながら、またまたアーチ構造のことをぼんやり考えていました。で閃いた事が一つ。今3連ラーメン架構があるとして、長期のモーメント図は、下に凸となった二次曲線が連なります。・・・・どこかで見たような形だな・・・ん?・・・こう・・・ひっくり返すと・・・・アーチじゃないか!!そうです。先人はこう考えたのでしょうか・・・「現に架構は、(今で言うモーメント図のように)曲がっている。理由は分からない。でも待てよ・・・同じように曲がったものを作って逆向きに据えれば、曲げようとしている力とちょうど相殺して、曲がらないのでは・・・。よしやってみよう。おー思ったとおり上手くいった。理由は分からないな。でもこれは使える!」こんな感じでしょうか。
現代に生きる我々は、ある現象について、とかくどうしてそうなるかを必死で考えるようになってしまっています。昔の人は違っていたのでしょう。物事を入口と出口で考える。ある不都合があるとする(入口)。こうすればいい(出口)。考え方には中間は省いている(理由は分からない。あるのは感覚だけ)。しかし入口と出口は押さえてあるから、全体を考えていることになる。そこには先日はな垂れがアーチ構造を述べるについて書いた「軸力」「曲げ」などの表立った知識はない。しかし彼らの意識や感覚の中にはそれがあった(たぶん)。現代人はどうか。入口と出口を押さえないから全体が分からない。しかも中間だけを考えてしまう。右往左往するうちに、そのうちに本来の目的も見失ってしまう・・・。
なるほど古代人のように考えるとは・・・こういう事を言いたかったのかのかもしれない・・・と想像しました。
尺貫法も知っていてよいのでは、と私は思います。尺貫法は、現代風に言えば、「人間工学的な」メジャーですから・・。
近代のある時期、建物の高さを100尺までにしよう、とした頃があったのです。たとえば東京・銀座通り。丸の内もそうでした。なぜかは分かりません。この位でいいんじゃない?ということだったのでしょう。でも、感覚的な判断はあったと思います。なぜなら、銀座も丸の内も、歩いていて威圧感は感じませんでしたから。
ところで、昔の人は、昔の人の方が、ある現象について、必死に考えていたと私は思います。今と違うのは、昔の人は、自分の体感、体験、経験、つまり自らの感性で考えた点です。今は、《教養》が邪魔をしているように思えます(感性が埋もれている・・)。