Google drive 力学・解析力学_物理会
高校物理、高校数学、微分方程式、ベクトル解析を前提として、YouTube上で力学・解析力学について15回にわたって説明した板書ノートのリンクです↑。2022年5月30日から2022年10月11日にかけて講義しました。
著作権は髙橋慧にあります © 2024 Kei Takahashi
主に、解析力学・量子論 第2版 (著者 須藤 靖)を教科書として使いました。
他の参考文献として、岩波基礎物理シリーズ 力学・解析力学 (著者 阿部 龍蔵)、詳解 物理応用数学演習 - 後藤 憲一 共編・ 山本 邦夫 共編・ 神吉 健 共編を用いた。
こちらのファイルに関する質問や指摘、コメントに関しては、実名による投稿のみ受け付けております。(匿名の場合はコメントを削除します)
メール(soudan.atamanonaka.2.718_attoma-ku_gmail.com)やTwitterのDM(@KayT0309)については匿名でも構いませんが、必ずしも返信するとは限りませんのでご了承ください。
【目標】
Newton力学、Lagrange形式、Hamilton形式のそれぞれを理解する。
【各回の概要】
1. 仕事とポテンシャル
力学が適応される範囲について。仕事、ポテンシャルの導入。
2. やりたいこと、仕事の定義とか
前回の補足、仕事の続き
3. 仕事続き、束縛条件
仕事の演習の続き、質点系の自由度として束縛条件の説明を行った。仮想仕事の原理についても理解した。
4. ラグランジュの未定乗数法、運動の三法則
仮想仕事の原理についてラグランジュの未定乗数法を用いて、平衡点を求める演習を行う。
運動の三法則をまとめて、ニュートン力学はここまで。
5. ガリレイ変換、ラグランジュ方程式導入
ニュートンの運動方程式を極座標で書き下し、運動方程式は極座標では煩雑な式になることを確認。
デカルト座標系でラグランジュ方程式を導入した。
6. ラグランジュ方程式導入
ラグランジュ方程式の共変性について理解した。
7. 保存則と角運動量
ニュートン力学に戻り、各保存則についてまとめた。
8. 角運動量演習、角運動量の一般化など
角運動量保存則導入と演習。n個の質点系へと一般化を行った。
9. 変分法
最小作用の原理からラグランジュ方程式を導出するため、変分法を説明。この回は物理数学の範囲ではある。上記した数学演習の演習書を使用した。
10. 変分法の練習
変分法を使った練習問題を解いた。この回も物理数学の範囲である。上記した数学演習の演習書を使用した。
11. 最小作用の原理、ニュートン力学導出
変分法を用いて最小作用の原理からラグランジュ方程式を導出。第一法則や質量などNewton力学を導出した。
12. 単振り子、エネルギー保存導出
単振り子の例として、Newton力学とLagrange形式の2通りで説明。一般化運動量を定義し、エネルギー保存則を導出し、Hamiltonianを導入した。
13. 各保存則、ネーターの定理
対称性から各保存則を導出。それらを一般化するネーターの定理を紹介した。
14. Hamilton形式の導入とLegendre変換
正準方程式、Hamilton形式の導入。また、Legendre変換の説明を行った。(cf. 包絡線)
15. Legendre変換続き、ポアソン括弧
ポアソン括弧を導入し、これまでのまとめを行った。
【総評・反省】
「力学?知ってるよ。早く解析力学やれよ」というのが、19歳大学1年生の私の一番最初の印象だった。
最近は微積物理とか呼ぶらしいが、微分積分によってニュートン力学をやってしまおうというのが受験界隈では流行っているので、まぁじゃああんまりそこはやらなくても良いかと思って、ニュートン力学を最小限で説明し、すぐに解析力学の分野に入った。高校生の頃からやたらに微積を使って物理学をやるのは私は反対であると表明しているはずなのだが…、我ながらなんともご都合主義な予定の組み方である。
本会においてニュートン力学で取り扱わなかった範囲として、回転座標系や慣性モーメントと剛体などかなり重要な部分を飛ばしてしまった。けれど正直、その後にはそんなに影響しなかったと思う。まぁ統計力学までやるにあたってはそんなに必要ないかとも思う。
解析力学に入って、正直この辺りから、割と私が「最短で良いとは思いつつも、とはいえ俺が説明しているわけだから、ここはちょっと厳密にしないと」ということが増えた気がする。聴講者のレベルをもう少し考えて、n個の質点系にこだわらなくても良かった気もする。(が、個人的には良いまとめになったし、勉強になった部分もあった笑)
量子力学をやるときに「え、ハミルトニアンってなんだよ」ってならなければそれで良い気もするが、とはいえ、その意味とか必要性とかを古典力学の範囲で知っていることは必要だと思うので、そこそこ詳しく説明したのだが、実際に量子力学に入ったときに「あー、正準変換説明してなかったわー」と何回か思ったのはちょっと反省点。
この回、ずっと「ぶっちゃけこれだけできれば良いじゃん!」と「とはいえ、ここは詳しくやるか」のせめぎ合いなのだが、それが(最初だからか)一番きつかったのが力学・解析力学であったように思う。
高校物理、高校数学、微分方程式、ベクトル解析を前提として、YouTube上で力学・解析力学について15回にわたって説明した板書ノートのリンクです↑。2022年5月30日から2022年10月11日にかけて講義しました。
著作権は髙橋慧にあります © 2024 Kei Takahashi
主に、解析力学・量子論 第2版 (著者 須藤 靖)を教科書として使いました。
他の参考文献として、岩波基礎物理シリーズ 力学・解析力学 (著者 阿部 龍蔵)、詳解 物理応用数学演習 - 後藤 憲一 共編・ 山本 邦夫 共編・ 神吉 健 共編を用いた。
こちらのファイルに関する質問や指摘、コメントに関しては、実名による投稿のみ受け付けております。(匿名の場合はコメントを削除します)
メール(soudan.atamanonaka.2.718_attoma-ku_gmail.com)やTwitterのDM(@KayT0309)については匿名でも構いませんが、必ずしも返信するとは限りませんのでご了承ください。
【目標】
Newton力学、Lagrange形式、Hamilton形式のそれぞれを理解する。
【各回の概要】
1. 仕事とポテンシャル
力学が適応される範囲について。仕事、ポテンシャルの導入。
2. やりたいこと、仕事の定義とか
前回の補足、仕事の続き
3. 仕事続き、束縛条件
仕事の演習の続き、質点系の自由度として束縛条件の説明を行った。仮想仕事の原理についても理解した。
4. ラグランジュの未定乗数法、運動の三法則
仮想仕事の原理についてラグランジュの未定乗数法を用いて、平衡点を求める演習を行う。
運動の三法則をまとめて、ニュートン力学はここまで。
5. ガリレイ変換、ラグランジュ方程式導入
ニュートンの運動方程式を極座標で書き下し、運動方程式は極座標では煩雑な式になることを確認。
デカルト座標系でラグランジュ方程式を導入した。
6. ラグランジュ方程式導入
ラグランジュ方程式の共変性について理解した。
7. 保存則と角運動量
ニュートン力学に戻り、各保存則についてまとめた。
8. 角運動量演習、角運動量の一般化など
角運動量保存則導入と演習。n個の質点系へと一般化を行った。
9. 変分法
最小作用の原理からラグランジュ方程式を導出するため、変分法を説明。この回は物理数学の範囲ではある。上記した数学演習の演習書を使用した。
10. 変分法の練習
変分法を使った練習問題を解いた。この回も物理数学の範囲である。上記した数学演習の演習書を使用した。
11. 最小作用の原理、ニュートン力学導出
変分法を用いて最小作用の原理からラグランジュ方程式を導出。第一法則や質量などNewton力学を導出した。
12. 単振り子、エネルギー保存導出
単振り子の例として、Newton力学とLagrange形式の2通りで説明。一般化運動量を定義し、エネルギー保存則を導出し、Hamiltonianを導入した。
13. 各保存則、ネーターの定理
対称性から各保存則を導出。それらを一般化するネーターの定理を紹介した。
14. Hamilton形式の導入とLegendre変換
正準方程式、Hamilton形式の導入。また、Legendre変換の説明を行った。(cf. 包絡線)
15. Legendre変換続き、ポアソン括弧
ポアソン括弧を導入し、これまでのまとめを行った。
【総評・反省】
「力学?知ってるよ。早く解析力学やれよ」というのが、19歳大学1年生の私の一番最初の印象だった。
最近は微積物理とか呼ぶらしいが、微分積分によってニュートン力学をやってしまおうというのが受験界隈では流行っているので、まぁじゃああんまりそこはやらなくても良いかと思って、ニュートン力学を最小限で説明し、すぐに解析力学の分野に入った。高校生の頃からやたらに微積を使って物理学をやるのは私は反対であると表明しているはずなのだが…、我ながらなんともご都合主義な予定の組み方である。
本会においてニュートン力学で取り扱わなかった範囲として、回転座標系や慣性モーメントと剛体などかなり重要な部分を飛ばしてしまった。けれど正直、その後にはそんなに影響しなかったと思う。まぁ統計力学までやるにあたってはそんなに必要ないかとも思う。
解析力学に入って、正直この辺りから、割と私が「最短で良いとは思いつつも、とはいえ俺が説明しているわけだから、ここはちょっと厳密にしないと」ということが増えた気がする。聴講者のレベルをもう少し考えて、n個の質点系にこだわらなくても良かった気もする。(が、個人的には良いまとめになったし、勉強になった部分もあった笑)
量子力学をやるときに「え、ハミルトニアンってなんだよ」ってならなければそれで良い気もするが、とはいえ、その意味とか必要性とかを古典力学の範囲で知っていることは必要だと思うので、そこそこ詳しく説明したのだが、実際に量子力学に入ったときに「あー、正準変換説明してなかったわー」と何回か思ったのはちょっと反省点。
この回、ずっと「ぶっちゃけこれだけできれば良いじゃん!」と「とはいえ、ここは詳しくやるか」のせめぎ合いなのだが、それが(最初だからか)一番きつかったのが力学・解析力学であったように思う。











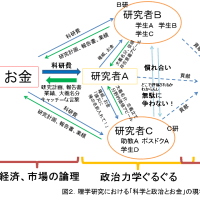
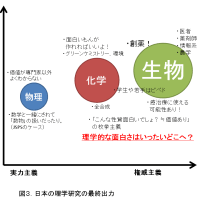
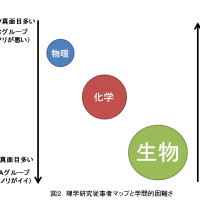

※コメント投稿者のブログIDはブログ作成者のみに通知されます