
図1
図1は新しい数独の問題です。今までブログに書いてきた
(1)数を入れる手筋 ①~④
(2)候補数を消す手筋 ①~④
を実行し、その事だけでは先に進まない状態を図2とします。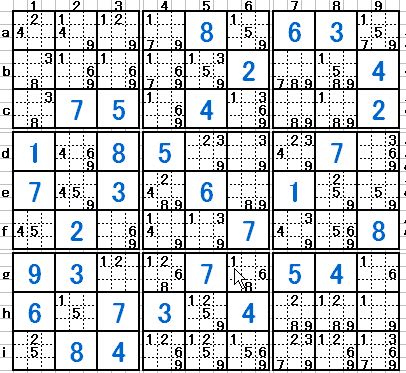
図2
⑤「隠れた2国同盟」の手筋が成立しないか、盤面を凝視します。少しお考え下さい。
マーちゃんが気が付く事とは違う事に気が付いた方もいる事でしょう。数独の解き方は人により千差万別!です。マーちゃんは下図3で説明します。
図3
図3のマスi7とi9(黄色印)に注目です。i行についての考察でもⅨブロックについての考察でも同じなのですが、説明の都合上Ⅸブロックについて考えます。
このブロックで3と7と8は候補数が2個。しかも3と7は同じマスに入っています。だから、i7=3が成立すれば、i9=7であり、i7=7が成立すれば i9=3 です。どちらの場合でも i7とi9はセットで3と7に”準確定”です。とすれば二つのマスを同時に含むi行とⅨブロックにはもはや3も7も入りません。言葉を変えて言えば、(この二つのマス以外のマスから)3と7を消去出来ます。
「自明の2国同盟」と何処が違うのか。「自明の2国同盟」の場合、マスに入る候補数は両マスとも2つで、目に見易い状態でしたが、「隠れた2国同盟」の場合、i7は候補数4個、i9は候補数5個と共に2個ではありません。その様にして、当該数(この場合3と7)以外の数に隠されているようにして「同盟」が成立していますから「隠れた2国同盟」と呼ぶ事にします。
外国の資料では「自明の2国同盟」のことを「naked pair」と言い、「隠れた2国同盟」の事を「hidden pair」と呼んでいます。
さて、この「隠れた2国同盟」は、こんなに遅くではなく、問題解決の早い段階で気が付く方が多いと思います。
それはユニット内(行・列・ブロック)の候補数が2個の場合、数に○を付けるのです。図4をご覧下さい。Ⅸブロックの拡大図です。
図4
このブロック内の③と⑦に注目すると「隠れた2国同盟」が簡単を簡単に発見できる、と言うわけです。(実はこの問題では初期段階は「隠れた2国同盟」は成立せず、局面が進んで「同盟」関係が成立しました)
この方法を使うと多くの問題は簡単に解けると豪語する方もいるほど強力な方法です。(ただ、候補数2個が行内か列内かブロック内かによって、以後の判断が違ってくるので、行内の2個は○、列内の2個は□、ブロック内の2個は△と違った印を用いましたが、煩雑なので止めて、マーちゃんは○で統一し、判断時に念には念を入れて「隠れた2国同盟」成立か否かを判断しています)。
さてこの「隠れた2国同盟」でi7とi9は3と7が、その位置(i7とi9)を占める事となりましたから、この二つのマスでは3と7を残し他の数は消去出来ます。また3と7が”準確定”となった結果を受けてi行とⅨブロックから、3または7が消去出来るマスがあるか否か読みますが、この場合更なる消去数はありません。その結果図5に至りました。
図5
明日から暫く、インターネット環境の無い所へ旅に出ますので、数日後から「第3章 中級ステップ」を書き始めます。



















