有馬温泉で指された第57期王位戦七番勝負第二局。
木村一基八段の先手で相矢倉。先手の早囲いに対して後手の羽生善治王位が7筋の歩を交換。先手も3筋の歩を交換して第1図のように進みました。
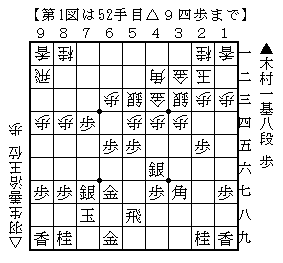
先手は後手の飛車を9筋に追いやっています。ですが後手の玉の方がずっとしっかりしています。先手がやり損っているのではないかと感じる局面でした。
▲5四歩と取り込み△同銀に▲5五銀とぶつけました。このまま交換するのは後手が損。△6五銀と歩を取るのも有力そうですが△4五銀と反対側に交わしました。
▲6六銀と引くのは固めつつ角筋を通す気持ちいい手ですが△3六銀と角取りに出られ▲9一角成△同飛▲5二飛成という進展になりました。

相手の飛車を僻地に追いやって龍を作るのは大きな戦果ですが,駒損も大きくて尋常な手段とは思えません。こういう勝負手がこの局面で必要であったなら,やはり第1図の時点では先手の作戦負けなのではないでしょうか。
羽生王位が勝って1勝1敗。第三局は来月9日と10日です。
第一部定義六がA群の定義であるなら,絶対に無限ということを認識するために必要とされる内容を説明するために不可欠であるものの定義に関しては,逆にA群であることはできず,B群でなければならないというのが僕の見解です。すなわちそれが無限に多くの属性から成っている実体と説明される必要があるなら,実体を定義した第一部定義三や属性を定義した第一部定義四はB群の定義でなければならないと僕は考えるのです。絶対に無限を認識するために,すでにそれらの認識が必須となっているなら,それらは単に実体なり属性なりといわれているだけでは不十分であり,スピノザが書簡九で記述していたいい回しに従えば,実体および属性を説明するのに必要な定義が要求されているといえるからです。
厳密にいえば,たとえば実体も属性もA群の定義であって,しかしそれら各々を説明するために必要な定義の中にB群のものが含まれているとしても問題はありません。ですがこういう循環は論理的には無限に継続することが可能で,最終的にB群の定義が要求されるのは間違いありません。なので僕はその循環を回避するために,第一部定義三と第一部定義四は,B群の定義であると解します。
これらがB群の定義であるならば,様態を定義した第一部定義五もB群です。第一部公理一の意味から,自然のうちには実体とその属性,そして様態だけが存在するのですから,実体の定義がB群なら様態の定義もB群でなければなりません。これはちょうど自由の定義がA群であるなら強制の定義もA群であるというのと同じ根拠です。
また,様態の定義がB群の定義である場合には,何らかの様態の定義についてもやはりB群であることが必要だと僕は考えます。したがって物体を定義した第二部定義一や観念を定義した第二部定義三もまたB群の定義でなければならないというのが僕の見解です。
『エチカ』のすべての定義について,それがA群に属するのかB群に属するのかということをここでは示しません。ですがここまでの説明から,僕がどのような条件でA群とB群を区分するのかということは理解してもらえたのではないかと思います。
木村一基八段の先手で相矢倉。先手の早囲いに対して後手の羽生善治王位が7筋の歩を交換。先手も3筋の歩を交換して第1図のように進みました。

先手は後手の飛車を9筋に追いやっています。ですが後手の玉の方がずっとしっかりしています。先手がやり損っているのではないかと感じる局面でした。
▲5四歩と取り込み△同銀に▲5五銀とぶつけました。このまま交換するのは後手が損。△6五銀と歩を取るのも有力そうですが△4五銀と反対側に交わしました。
▲6六銀と引くのは固めつつ角筋を通す気持ちいい手ですが△3六銀と角取りに出られ▲9一角成△同飛▲5二飛成という進展になりました。

相手の飛車を僻地に追いやって龍を作るのは大きな戦果ですが,駒損も大きくて尋常な手段とは思えません。こういう勝負手がこの局面で必要であったなら,やはり第1図の時点では先手の作戦負けなのではないでしょうか。
羽生王位が勝って1勝1敗。第三局は来月9日と10日です。
第一部定義六がA群の定義であるなら,絶対に無限ということを認識するために必要とされる内容を説明するために不可欠であるものの定義に関しては,逆にA群であることはできず,B群でなければならないというのが僕の見解です。すなわちそれが無限に多くの属性から成っている実体と説明される必要があるなら,実体を定義した第一部定義三や属性を定義した第一部定義四はB群の定義でなければならないと僕は考えるのです。絶対に無限を認識するために,すでにそれらの認識が必須となっているなら,それらは単に実体なり属性なりといわれているだけでは不十分であり,スピノザが書簡九で記述していたいい回しに従えば,実体および属性を説明するのに必要な定義が要求されているといえるからです。
厳密にいえば,たとえば実体も属性もA群の定義であって,しかしそれら各々を説明するために必要な定義の中にB群のものが含まれているとしても問題はありません。ですがこういう循環は論理的には無限に継続することが可能で,最終的にB群の定義が要求されるのは間違いありません。なので僕はその循環を回避するために,第一部定義三と第一部定義四は,B群の定義であると解します。
これらがB群の定義であるならば,様態を定義した第一部定義五もB群です。第一部公理一の意味から,自然のうちには実体とその属性,そして様態だけが存在するのですから,実体の定義がB群なら様態の定義もB群でなければなりません。これはちょうど自由の定義がA群であるなら強制の定義もA群であるというのと同じ根拠です。
また,様態の定義がB群の定義である場合には,何らかの様態の定義についてもやはりB群であることが必要だと僕は考えます。したがって物体を定義した第二部定義一や観念を定義した第二部定義三もまたB群の定義でなければならないというのが僕の見解です。
『エチカ』のすべての定義について,それがA群に属するのかB群に属するのかということをここでは示しません。ですがここまでの説明から,僕がどのような条件でA群とB群を区分するのかということは理解してもらえたのではないかと思います。













