棋聖戦＆個別的対応

　豊田市で指された第85期棋聖戦五番勝負第二局。
　羽生善治棋聖の先手で相矢倉。類例の少ない形でしたが,先手が攻めて後手が受けつつカウンターを狙うという,この戦型で最も多く生じるパターンに。この将棋は森内俊之竜王が入玉もひとつの狙いとする進展に。
　　　　　　　　　　　　　　　　　　　　　　　　　
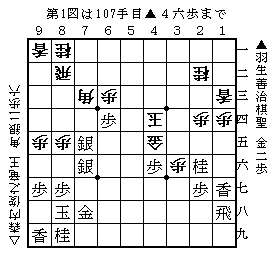
　たぶんひとつの分岐で,△３七歩成▲４五歩△３五玉から一直線に入りにいく順もあったかと思います。ただ金を取られるのを嫌って△同金も普通の手といえるでしょう。ただこのために角の行き場がなくなり,▲６三歩成以下の手順で角を取られることになりました。進んで第2図。
　　　　　　　　　　　　　　　　　　　　　　　　　
　入玉しきれずに後手は中団で徹底抗戦。ここから▲４七歩△同金▲６七銀と進めたのがうまい手順で,先手が勝ちを決めたように思います。このまま▲５六銀と使われてはいけないと△５五銀と打ったのですが,▲同金△同角▲同馬△同金▲７一角で王手飛車。△４四銀に飛車を取るのではなく▲３三銀と打ったのが,最後の決め手でした。
　　　　　　　　　　　　　　　　　　　　　　　　　
　これで６七に引いた銀が５六に出ていく目途が立ち,後手は振りほどけなくなりました。持ち駒の少ない第2図からの盤上の駒の使い方が光った一局だったと感じます。
　羽生棋聖が連勝。第三局は来月5日です。

　一般論が解決法となり得ないのであれば,個別的に対応していくほかありません。たとえばある有限である事物,『エチカ』では個物res singularisということになりますから,あるres singularisを任意に抽出し,そのres singularisのうちに何らかの意味において無限性を見出すことが可能になれば,少なくともそのres singularisについては,それを無限であるとするテーゼが成立し得るということになります。そしてこうしたテーゼが抽出されるどのような個物にも適用可能であるなら,総合的な意味において有限であるものは無限であるというテーゼが成立し得るということになるでしょう。
　まず,第一部定理二五系に注目してみましょう。そこでは個物res particularisが,神の属性を一定の仕方で表現するといわれています。このとき,ふたつの個物res particularisとres singularisに同一の訳を与えてよいか否かということは,ここでは問題にする必要がありません。仮に同一の訳を与えることを可とする僕の解釈が誤りであったとしても,その場合にはres singularisよりもres particularisの方が広きにわたる概念であり,res particularisのうちにres singularisが含まれるということになるからです。そうであるなら,res particularisが神の属性を一定の仕方で表現するということのうちに,res singularisが神の属性を一定の仕方で表現するという意味合いが含まれていることになります。今はこの条件さえ確保されていれば十分です。
　第一部定義六は,属性が無限性を表現するといっています。端的にいってこれは属性が無限であるということの表明であるといえます。ただし,第一部定義六説明のテクストからして,ある単一の属性は,絶対に無限ではないということになります。その属性は他の属性によって否定されるからです。したがって属性というのは,自己の類において無限であると解釈されることになります。