日々適当

最近、三角関数を教える必要性の是非云々でちょっと騒がしかったわけですけど、その是非はともかく、こんな風に役に立つってことで流れてきた情報に、うぎゃーって思ったものが一つあったので…

イーズイン・イーズアウトさせるようなカーブを簡単に書く式にcosがいい感じっての。



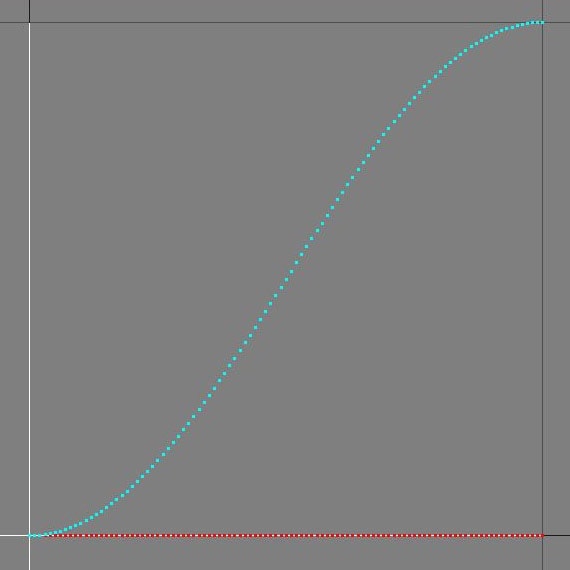
赤点で書かれた0から1の入力が、簡単な数式通すと青点のS寺カーブになりますよ、ってのね。



なるほど、考えりゃそうですよねって式でした。

これをフーなんとかですぐに実装できるようになりたいものだ。

まことにお恥ずかしい事ですが、なぜか、水平画角と垂直画角の比はフィルムサイズが変わらなければ一定だと思っておりました。フィルムのサイズが16:9なら画角の比も16:9だろうと…。

アホでした。

水平画角：fovx
垂直画角：fovy

フィルムサイズの縦を H 、横を W 、焦点距離をLとすると、

fovx = 2 * atan( W/2L )
fovy = 2 * atan( H/2L )

となりますわな。ここから、fovyが分かっているとき、fovxは

fovx = 2 * atan(W/H * tan( fovy / 2 ))

fovxが分かっているときのfovyは

fovy = 2 * atan(H/W * tan( fovx / 2 ))

となりまする。5度ずつfovxの値を変えたときのfovyと、fovx/fovyの値は下表の通り。

fovx	fovy	fovx/fovy
1	0.562509761	1.777746928
5	2.813720613	1.777006565
10	5.634776631	1.774693241
15	8.470562218	1.770838772
20	11.32858959	1.765444837
25	14.21654933	1.758513928
30	17.14237226	1.7500495
35	20.11429322	1.740056168
40	23.14091714	1.72853996
45	26.23128755	1.715508624
50	29.3949576	1.700972006
55	32.64206323	1.684942512
60	35.98339777	1.667435643
65	39.43048686	1.648470642
70	42.99566142	1.628071245
75	46.69212571	1.606266557
80	50.53401585	1.583092075
85	54.53644225	1.558590852
90	58.71550709	1.53281483
95	63.08828456	1.50582633
100	67.67274797	1.477699709

全然一定じゃない。
アホでした…。

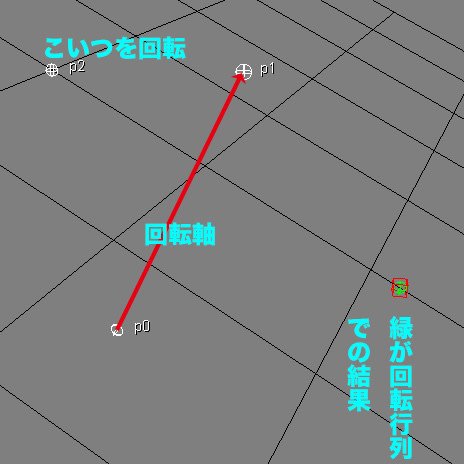
こんな感じでp0、p1、p2の3つの点があって、p0からp1へのベクトルを回転軸としてp2を回してみましょうって時、どうするか。
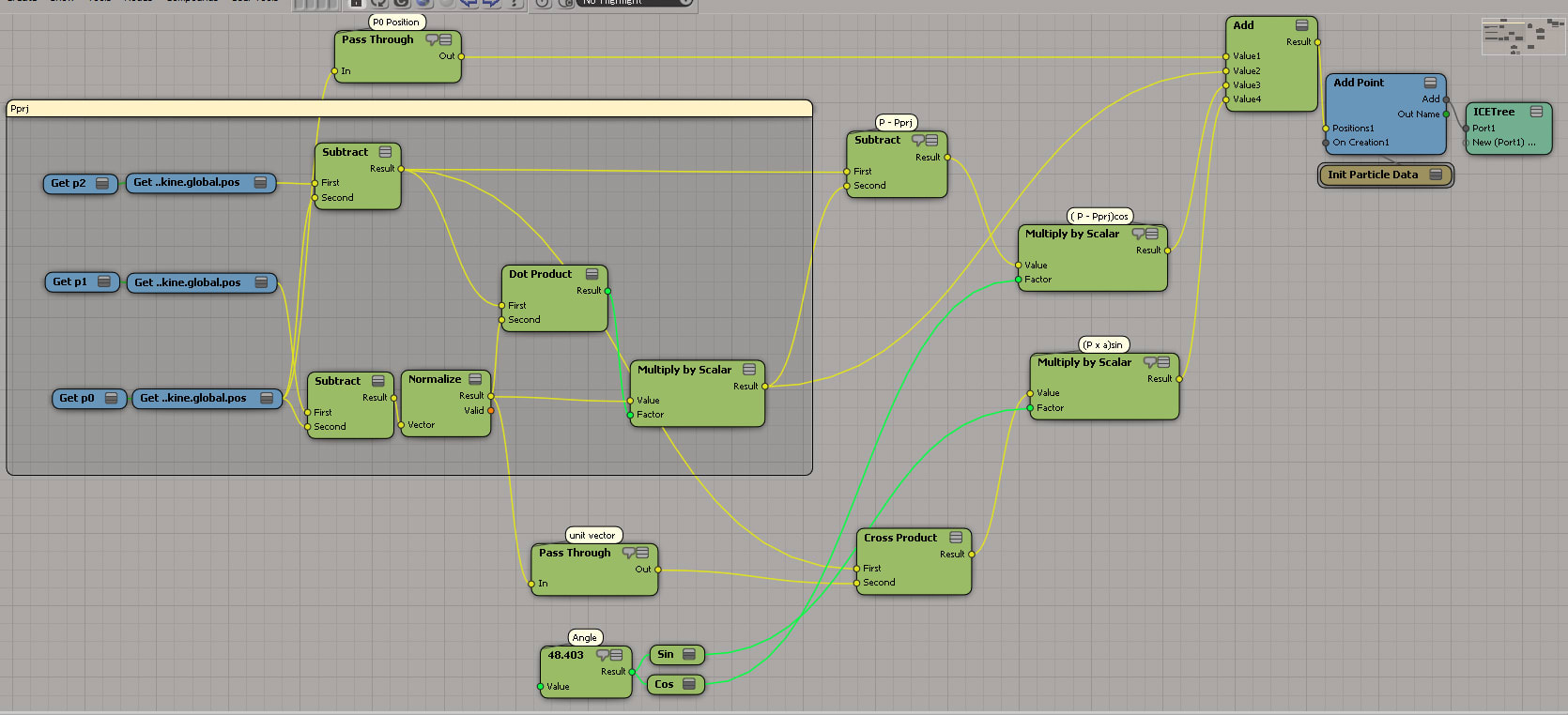
これは単純にベクトルのたし算でできちゃいます。ICE Treeはこんな感じ。



詳しくは、こーいうところを見るのがいいでしょうかね（丸投げ）。

３次元の回転 (原点を通る任意方向回転軸，座標系に依存しないベクトル・回転行列表現 )

ところで、これを変形していくと、回転行列が求められます。うん、求められるらしいですよ？w



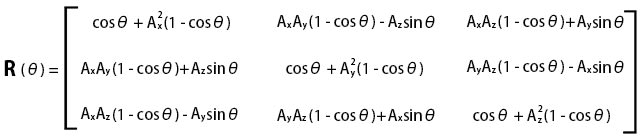
回転軸上の単位ベクトルを (Ax, Ay, Az) として、θ度回転している時の式です。
これをICE Treeに実装すると、



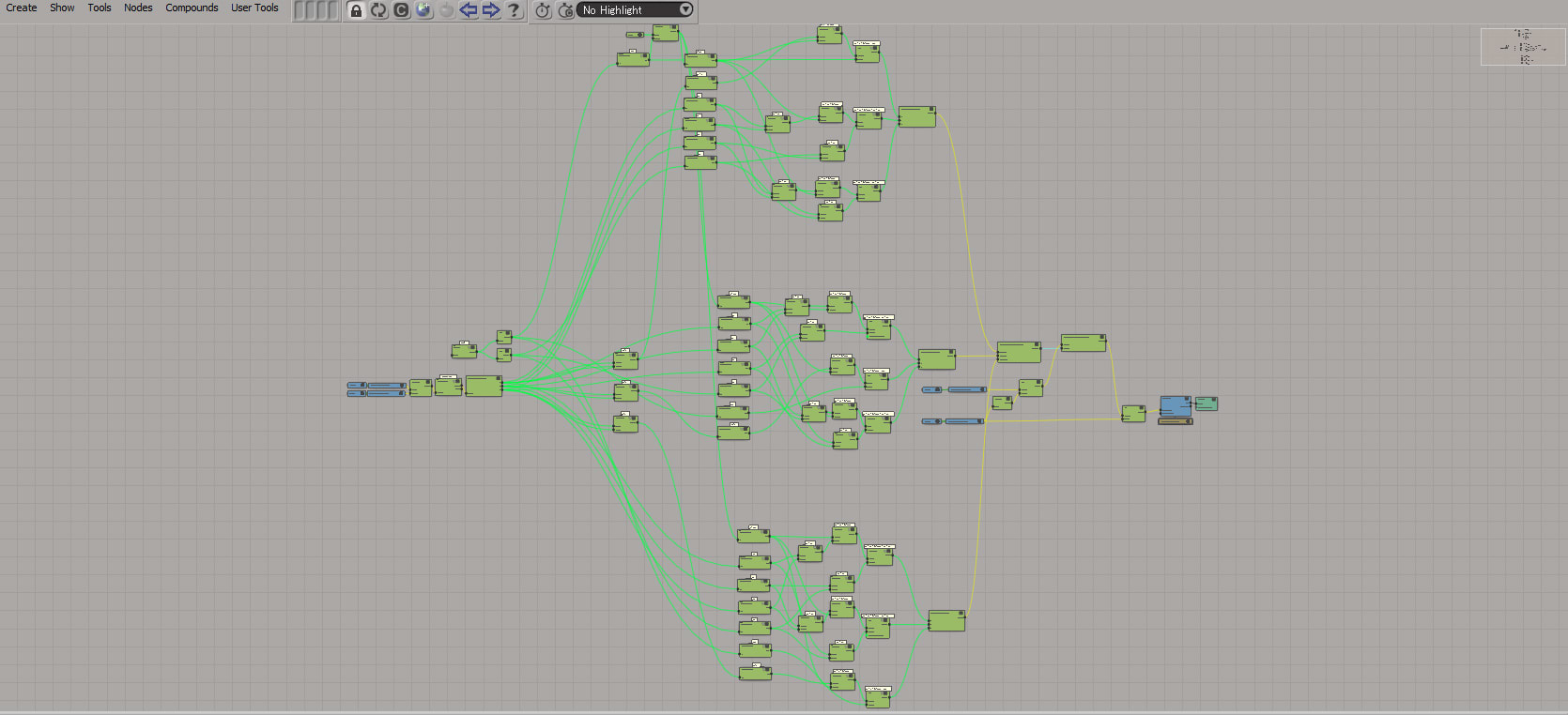
と非常に煩雑になります。でも、これを正しくかければ、いい感じに行くようですね。
上記ICE Treeは回転軸がp0→p1なので、p2の位置を、p0を原点に戻す量だけ動かした上で、上記回転の変換をかけ（Multiplay by Matrixを使います）、出てきた結果に対してまたp0の位置分だけ動かしてやるという手順を踏んでいます。

ってことで、これをスクリプト実装してやれば、「スライスツールをスクリプトから設定することを考える [日々適当] 」こいつがちゃんとできるはずです。たぶん、以前実装した時はp0分だけ動かしてやることをしていなかったのが悪かったのでは無いかと想像していますがどうですかね。

ポリゴンの面積を求めてみようと思います。
周知の通り、Softimageで通常扱うポリゴンは3点以上の頂点からなっています。つまり、三角形の集まりと考えることが出来るわけです。そこで、三角形の分割して、その和を求めてやればよい、という簡単な話になります。

ただし、三角形に分割してというお話はあまり簡単ではなさそうです。



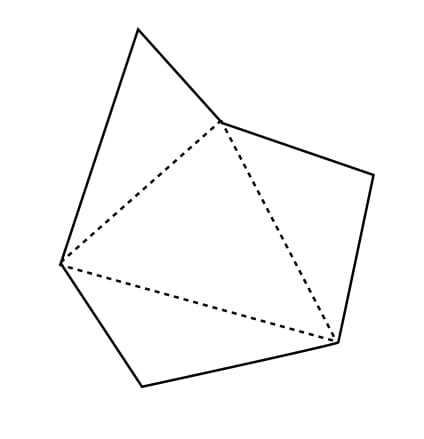
例えば、こんなふうに三角形に分割できればいいんですけど、それを実装するのはちょっと面倒そうなんですよね。この三角形を構成する頂点はどれだろうというのを見つけだすのが大変そうなのですよ。
そこで、任意の一点と多角形の各頂点を結ぶ三角形を考えます。



こうすると、ポリゴンを構成する頂点を順番にたどっていけば良いことになり、先の考え方よりずいぶんと簡単そうです。上図のように、任意の一点が多角形の内側にあれば分かりやすいのですけど、その一点が外側にあってもこの考え方は成立するようです。

要するに、下図の水色の面積を求めるには、緑色の部分から黄色の部分を引けばいいわけなのですよ。





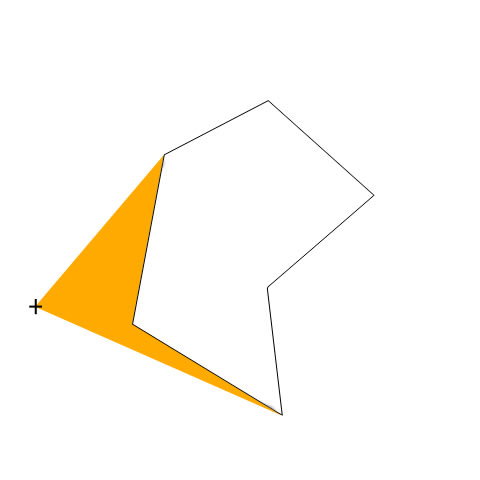
以下、非常にゆるーい書き方になります。なんとなく。

外積です。
2つのベクトルの外積で得られるベクトルの長さは、そのベクトルで作られた平行四辺形の面積に相当する、というのがあります。



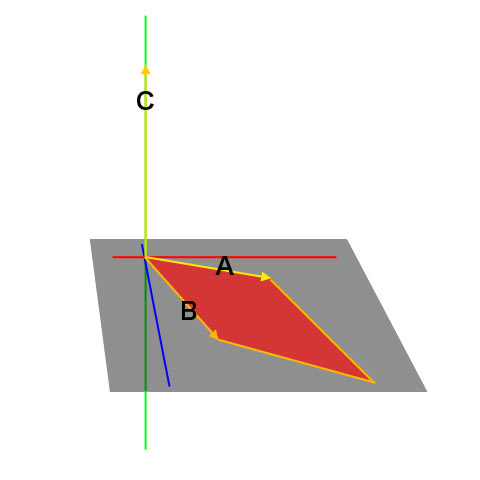
上図の赤く塗りつぶされた部分が、ベクトルAとベクトルBの外積（ベクトルC）の長さに相当する部分ってことっすね。
んで、Cの向きはA x Bの時とB x Aの時では逆になります。

下図の多角形abcdefにおいて、任意の一点をpに決めた時、青い三角形cdpと赤い三角形fapについて考えてみます。



頂点の並び順通りにベクトルの向きを考慮していくと、青い三角形はベクトルcdとベクトルcpの外積の長さの半分の値が面積に、赤い三角形はベクトルfaとベクトルfpの外積の長さの半分の値が面積になります。例えば右手の親指をcdに合わせて、ひとさし指をcpに合わせると、中指は画面手前側に曲げられると思います。親指をfaにひとさし指をfpに合わせると中指は画面奥に曲げることが出来ます。
雰囲気として、外積で得られるベクトルの向きが逆になっていることが分かるんじゃないでしょうか(^^)

というわけで、青い三角形連中で形作られるのが前述した「緑色の部分から黄色の部分を引けばいい」の緑色にあたり、赤い三角形連中で形作られるのが黄色にあたるんで、多角形の面積は、多角形の各辺に相当するベクトルと、頂点から多角形と同一平面上の一点へのベクトルとの外積の長さの和の半分の値になると言えるんじゃないか、となります。ただし、外積で得られるベクトルの向きが逆なら、長さをマイナス値にしてやります。

上図の場合、頂点aとbを結ぶベクトルを (ab) のように表し、ベクトルVの長さを length (V) とか書いてやるとするなら
( length((ab)x(ap)) + length((bc)x(bp)) + length((cd)x(cp)) + length((de)x(dp)) + length((ef)x(ep)) + length((fa)x(fp)) )/2
ということっすね。efとfaの部分はベクトルが逆だからlengthで出てくる値もマイナスってことで一つお願いします。

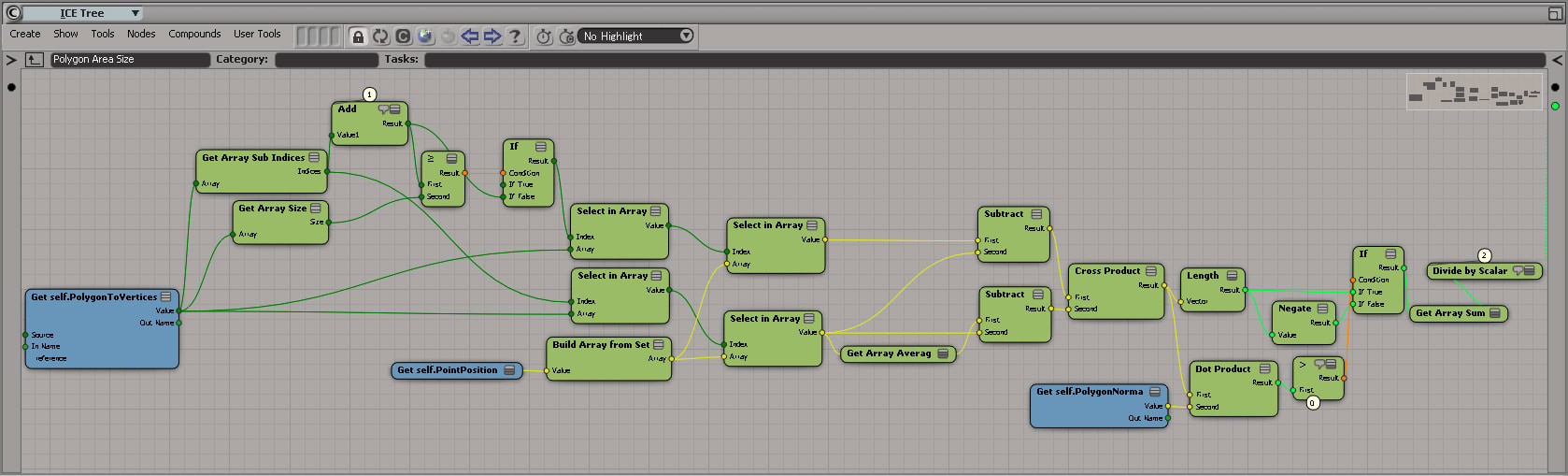
これをICEで実装してみました。なお、任意の一点はポリゴンがゆがんでいることを考慮せずに、ポリゴンを構成する頂点位置の平均の位置に設定しています。



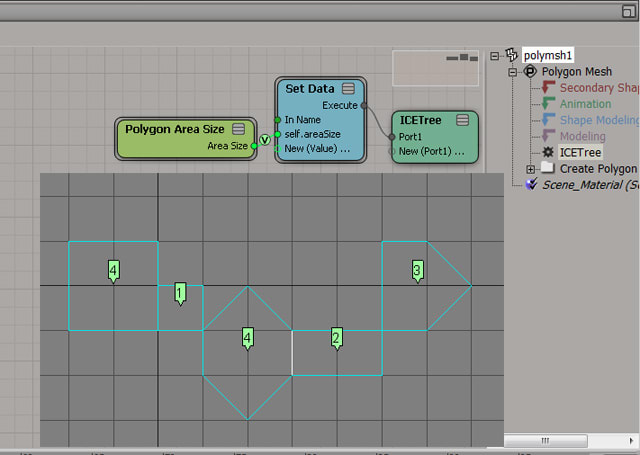
コンパウンドの中身は以下の通り。符号の向きはポリゴンの法線と外積の向きが同じか否かで判断します。



ポリゴンがゆがんでいると（すべての頂点が同一辺面上に無いと）、値が狂ってきますけど、まぁ、きっちりとした値を出す必要が無く、モデルもそんなにゆがんでいないトポロジーなものなら、何とかつかえるんじゃないかなー。
あ、いくつかある Select in Arrayノードのうち、一番左下のヤツいらないじゃんw

3乗根とかいうけど、ルートの記号の左側に3とかかれているものっすね。

こいつを解こうとするときは、1/3乗してやればよい、というお話です。



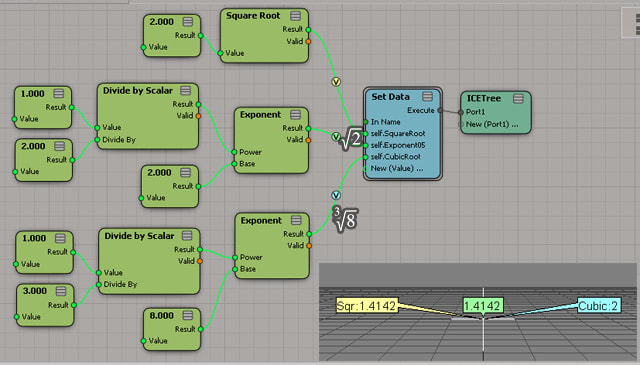
そんだけですけど、ICEで組むとき、立方根のノードやコンパウンドは用意されていないので、理屈が分からなくても、この考え方を知っておく事は大切なんだろうなぁ。

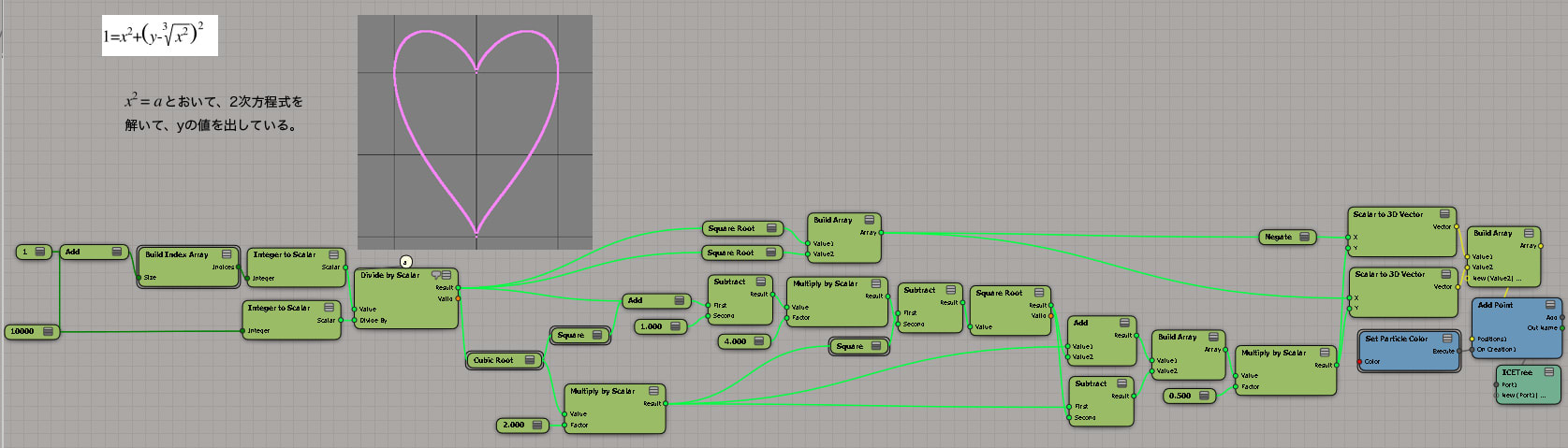
へこむわー

平面を表す式は

ax + by + cz + d = 0

とかなんとか。しかして、法線が分かっているなら、その法線ベクトル

N = ( nx, ny, nz）

を利用して、

nx*x + ny * y + nz * z - (nx*xp0 + ny*yp0 + nz * zp0) = 0

とか表すことが出来ます。あ、(xp0, yp0, zp0) は平面上の任意の一点ね。

一方、直線を表す式は、直線に平行な単位ベクトルを (ax, ay, az) 、直線上の任意の点を (xl0, yl0, zl0) として、

(x - xl0)/ax = (y - yl0)/ay = (z - zl0)/az

と表すようです（ベクトル云々でこの式は導けます）。

んじゃ、この交点はというと、まず、直線の式を、

(x - xl0)/ax = (y - yl0)/ay = (z - zl0)/az = t

とおいて、

x = ax * t + xl0
y = ay * t + yl0
z = az * t + zl0

とした上で、これを平面の式に代入します。

nx * (ax * t + xl0) + ny * (ay * t + yl0) + nz * (az * t + zl0) - (nx * xp0 + ny * yp0 + nz * zp0) = 0

tについて解くと、

t = ((nx * xp0 + ny * yp0 + nz * zp0) - (nx * xl0 + ny * yl0 + nz + zl0))/(nx * ax + ny * ay + nz * az)

ってことで、

x = ax * ((nx * xp0 + ny * yp0 + nz * zp0) - (nx * xl0 + ny * yl0 + nz + zl0))/(nx * ax + ny * ay + nz * az) + xl0
y = ay * ((nx * xp0 + ny * yp0 + nz * zp0) - (nx * xl0 + ny * yl0 + nz + zl0))/(nx * ax + ny * ay + nz * az) + yl0
z = az * ((nx * xp0 + ny * yp0 + nz * zp0) - (nx * xl0 + ny * yl0 + nz + zl0))/(nx * ax + ny * ay + nz * az) + zl0

とか何とか。すっかり忘れているけど高校の数学なんだと思う。

んじゃ、これを実装しましょう。

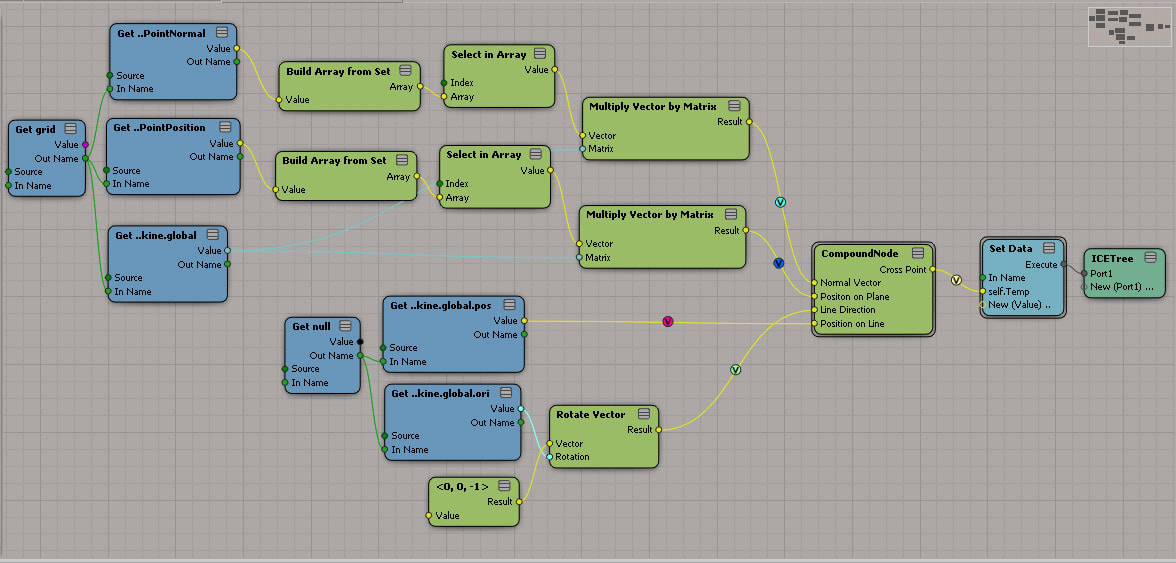
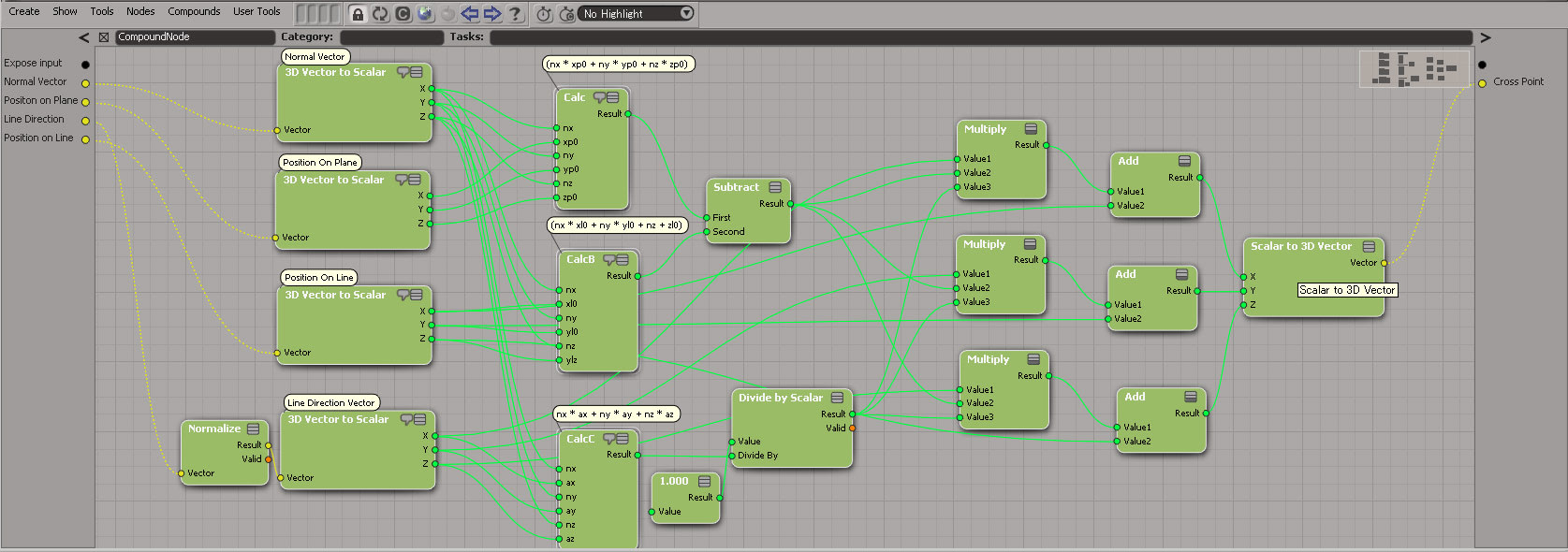
ツリーとしてはこの程度。ただし、上記数式はコンパウンドないで実装しています。



そのまんまですね。しかし、これでとりあえずうまくいっているようです。



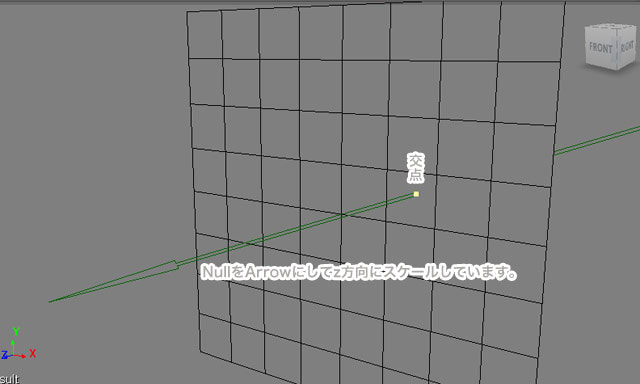
とか考えていたのはですね。raycastノードって対象にヒットしないと使えないんですよね。当たり前ですけど。けど、対象がグリッドの時、そのグリッドを無限平面と見立てて交点を知りたいシチュエーションがあったりしたんですよ。

まぁ高校数学の役に立つこと…。復習しないと（復習ってより、新たに学び直すに近いな(^^;）

モルワイデ図法を表す式は、ただしソースはウィキペディアによると、地球の半径を1とし、地図にしたときの赤道上の縮尺を1にする場合、経度をλ、緯度をΦとして、



ただし、θは



を満たす値、との事です。λ、Φ、θ、いずれもラジアン単位です。

正距円筒図法をモルワイデ図法に変形する場合には、正距円筒図法の座標をそのまま経緯度の値に読み替える事が可能ですから、λとΦの値は明らかなので、θの値を出す事が出来ればOKという事になります。

んじゃ、θの値をどうやって出すか、というわけっすね。先のθの条件式の要素を全部片方に集めます。



すなわち、



こいつのyが0になるときのxが分かればいいってことっすね。

ってことで、ニュートン法とやらを試します。
ニュートン法は、y = f(x) について y = 0の時の x の値を近似して導く事が目的の物のようですね。

求める点付近のx値 x0 について、yの値はf(x0)。この点における y = f(x)の接線がx軸と交わる時のxの値がx1。このときのyの値がf(x1)。この点における y = f(x)の接線がx軸と交わるときのxの値がx2・・・・・・

といった作業を繰り返すと、正しいxの値に収束していく、という考え方みたいです。もちろんすべての場合でこれが成り立つわけじゃないけど、今回の目的には使えそうです。



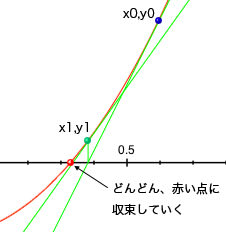
接線がx軸と交わる時のxの値は、x = xnの時の接線の式が

y - f(xn) = f'(xn) * (x - xn)

だから（だからぢゃねーよって感じだけど、検算するとちゃんとそうなったよ）、

xn+1 = xn - f(xn)/f'(xn)

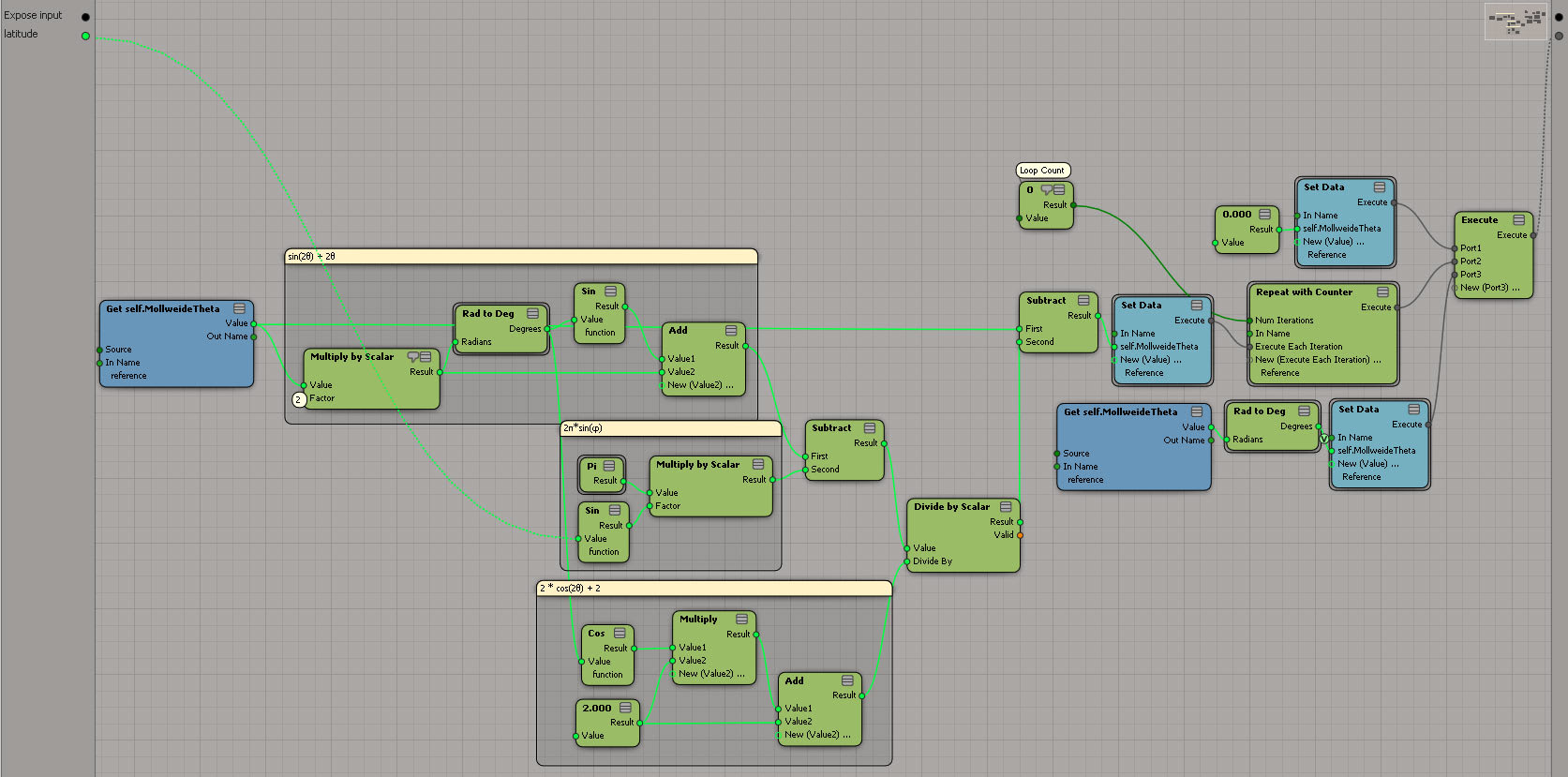
ってことで組んだICE Treeはこんな感じ。



こいつのlatitudeと名付けたポートに緯度の値Φを入れてやって出てくる値は、



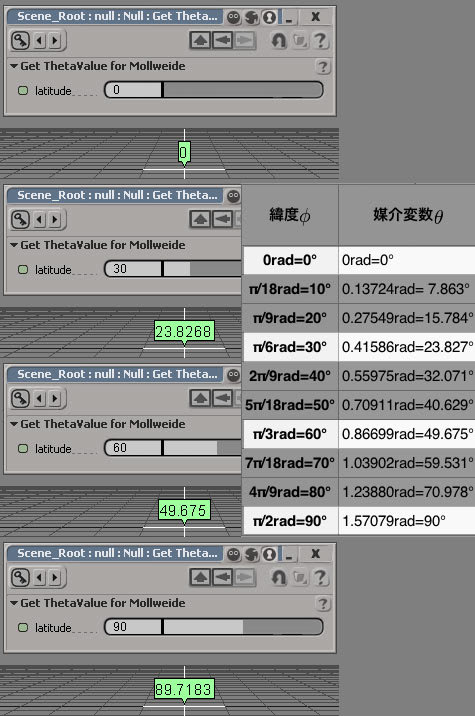
こんな感じで、ただしソースはウィキペディアに書かれている値とだいたい一致しまする。

初期値が0なので、ここの値の取り方やリピートの回数によって結果が変わりますけど、まぁ、だいたいこんな感じで、だいたいモルワイデ図法を作る事が出来ました。

平面上における円の式は

x = r * cosθ
y = r *sinθ

でいいわけっすよね。角度をパラメータとして座標を出している。
これを立体に適用すると球になります。

角度は経度・緯度の二つをパラメータとします。それぞれ、θとγとします。

x = r * cosθ * cosγ
y = r * sinγ
z = r * sinθ * cosγ

yアップだと幸せなので、平面をxz、高さをyと考えている場合の式です。そのため、先の円の式のyの式はzに適用しています。x、zの値にはcosγがかけられていますけど、これは緯度が高くなるほどに緯線の円の直径が小さくなる事を表しております。yの値は緯度の高さなんで、sinγっすね。

ってことで、幅360、高さ180のグリッドを球に変形します。



素直に実装するとこんな感じ。このままだと、xyの符号が想定の逆になるんで、Negateノードかますとよいでしょ。これをどんなグリッドにも適用するなら、PointPositionが緯度・経度の値になるように補正してやればいいってことっすな。



さて。問題はこの変形途中をいかに自然にできるかってことでして。

非常に初歩的なことっすが。

2次元の直線が交差しているか否かを調べるICE Compoundを考えてみたり。
といってもネット上の情報を参考に作っただけだけどね。

考え方は、点A, Bを結ぶ直線ABと、点C,Dを結ぶ直線CDについて考えるとき、この2直線が交差している場合、直線ABに対して、点CとDはそれぞれ逆側にいるはず、という理屈を元にしています。

つまり、図で示すと



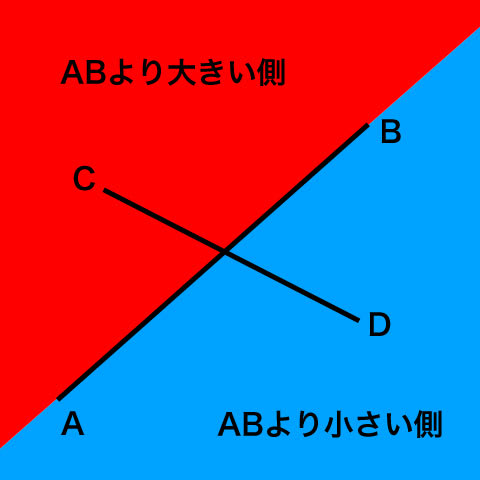
交差している場合なら、CとDはそれぞれABを基準にして反対側にある。



交差していないなら、ABに対してどちらか側に偏ってCとDは存在する。

CDに対してAとBがどうかも調べてやって、この場合も「反対側に存在する」という状態なら、ABとCDは交差している、と言える、という理屈です。

ABの場合のチェックだけの場合、AとBを通る直線とCDが交差するか否かしか判断できません。CDの場合だけの場合もそうですね。だから、ABとのCDとの交差を調べるなら、両方の場合のチェックが必要のようです。

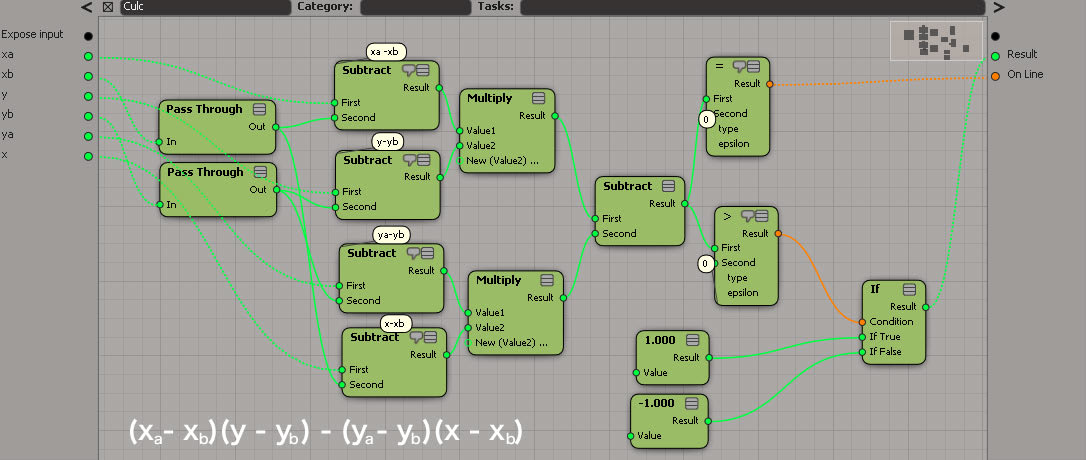
というわけで、組んだツリーはこんな感じ。



コンパウンドの中身。



Culcコンパウンドの中身。



で、このICE Treeの結果。



線上にある場合も一応考慮してある作りです。

そんな感じ。

<追記>
こーいう考え方でもいいのかな？


</追記>

<追記>


3Dに拡張してみた。一気に面倒くさくなるね。
</追記>

5x1 + 3x2 + x3 = 3
4x1 + 5x2 + 2x3 = 4
x1 + 3x2 + 6x3 = 6

この連立一次方程式の(x1,x2,x3) の値を求める方法。

これを行列を使って書くと各要素を以下のようにして、



y = Ax

になりまする。両辺にAの逆行列をかけるとxが求まりまする。
つまり、ICEで記すとこんな感じ。

ふむ。