先日、「おりがみパヅル」なるパズルを公開しました(こちら)。
公開したのはいいんですが、かなり難しいパズルなので、実際チャレンジしてくれる人はいないだろうと思ってました。
が、嬉しいことにいたんですよねぇ。
やっぱりパズルを考案した以上はチャレンジしてくれる人がいるのはありがたいことです。
ただかなり苦戦しているみたいなので今日は簡単にこのおりがみパヅルの解き方についてレクチャーをしたいと思います。
おりがみパヅルは次のようなものでした。

Q)一枚の正方形の紙に切り込みを入れて連鶴を折ります。このとき紙を余らせず、また鶴の翼と翼のみが繋がっているものとします。11連になるような分割を求めなさい。
この問題を簡単なものとします。
Q)一つの正方形を大きさの異なる十一個の正方形に分割するものとします。どのような分割が考えられるか答えなさい。
最初の問題だと連鶴というものの概念がわかってないと問題そのものの意味がわからなかったと思いますが、二つ目の問題だと連鶴の要素を削ったので、正方形の概念さえわかっていれば問題に取り組めると思います。ただ、最初の問題が答えが一つだったのに比べ、二つ目の問題は複数解になりますけどね。
次のような解が求められます。
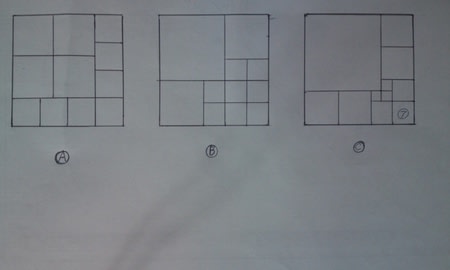
一番シンプルな解はⒶでしょう。大きな正方形四つと小さな正方形七つで一つの正方形を構成しています。これぐらいだと正方形に線を引いていって解を求めることが出来ると思います。
Ⓑでも出来ないことはないでしょう。
しかしⒸぐらい複雑だと正方形に線を引いていくやり方ではこの解にたどり着かないはずです。
ではどうするか?
問題には「分割せよ」というふうに書いてあります。
なので素直な人は大きな正方形をまず書いて、それに線を引いていって答えを求めようとするでしょう。
そのやり方が違うんです。発想を変えます。
Ⓒを見てください。右下隅にアと書いてありますね。
この核となる正方形アの上と左に同じ(もしくは異なる)大きさの正方形をくっつけます。
そうしていくことで最終的に十一個の正方形で一個の正方形を構成するようにするのです。
十一個の正方形で一個の正方形を構成する、その組み合わせも実は多くありません。
五つか、六つか、といったところだと思います。
すべての組み合わせがわかれば、最初の問題の解も確実にその中に含まれているはずです。
健闘を祈ります!
公開したのはいいんですが、かなり難しいパズルなので、実際チャレンジしてくれる人はいないだろうと思ってました。
が、嬉しいことにいたんですよねぇ。
やっぱりパズルを考案した以上はチャレンジしてくれる人がいるのはありがたいことです。
ただかなり苦戦しているみたいなので今日は簡単にこのおりがみパヅルの解き方についてレクチャーをしたいと思います。
おりがみパヅルは次のようなものでした。

Q)一枚の正方形の紙に切り込みを入れて連鶴を折ります。このとき紙を余らせず、また鶴の翼と翼のみが繋がっているものとします。11連になるような分割を求めなさい。
この問題を簡単なものとします。
Q)一つの正方形を大きさの異なる十一個の正方形に分割するものとします。どのような分割が考えられるか答えなさい。
最初の問題だと連鶴というものの概念がわかってないと問題そのものの意味がわからなかったと思いますが、二つ目の問題だと連鶴の要素を削ったので、正方形の概念さえわかっていれば問題に取り組めると思います。ただ、最初の問題が答えが一つだったのに比べ、二つ目の問題は複数解になりますけどね。
次のような解が求められます。

一番シンプルな解はⒶでしょう。大きな正方形四つと小さな正方形七つで一つの正方形を構成しています。これぐらいだと正方形に線を引いていって解を求めることが出来ると思います。
Ⓑでも出来ないことはないでしょう。
しかしⒸぐらい複雑だと正方形に線を引いていくやり方ではこの解にたどり着かないはずです。
ではどうするか?
問題には「分割せよ」というふうに書いてあります。
なので素直な人は大きな正方形をまず書いて、それに線を引いていって答えを求めようとするでしょう。
そのやり方が違うんです。発想を変えます。
Ⓒを見てください。右下隅にアと書いてありますね。
この核となる正方形アの上と左に同じ(もしくは異なる)大きさの正方形をくっつけます。
そうしていくことで最終的に十一個の正方形で一個の正方形を構成するようにするのです。
十一個の正方形で一個の正方形を構成する、その組み合わせも実は多くありません。
五つか、六つか、といったところだと思います。
すべての組み合わせがわかれば、最初の問題の解も確実にその中に含まれているはずです。
健闘を祈ります!



























でも、とてもとても難しくて、くじけそ~でした。
このヒントを頼りに、もう少し頑張ってみますね。
1人でもチャレンジしてくれる人がいるということは嬉しいことですね。
でもこうなると答えを発表するのが怖くなりますね。
「なるほど!」といってもらえたらいいけど、「そんな答えアリなんですか?」と言われる可能性も無きに非ずなので。
なので頑張って蒼史さんには自力で解いて欲しいです。笑。