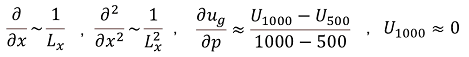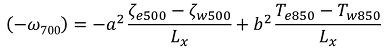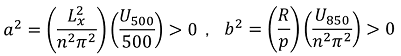観測史上最早の梅雨明け

　2022年の「梅雨」はアッという間でした。北陸地方は6月28日に「梅雨明け」が発表され、翌29日には東北南部でも「梅雨明け」が発表されました。

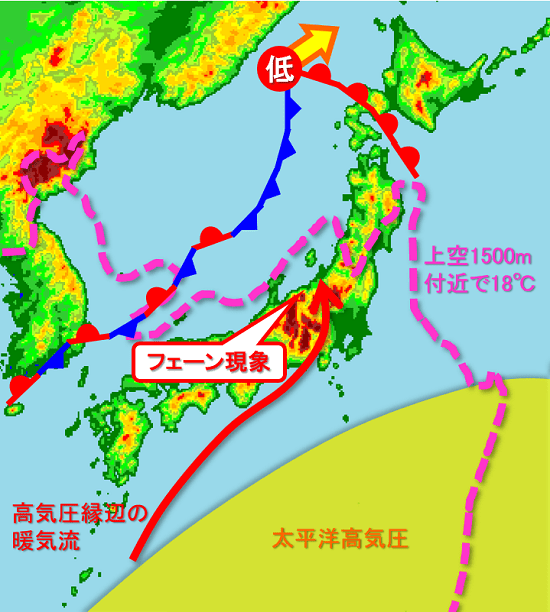
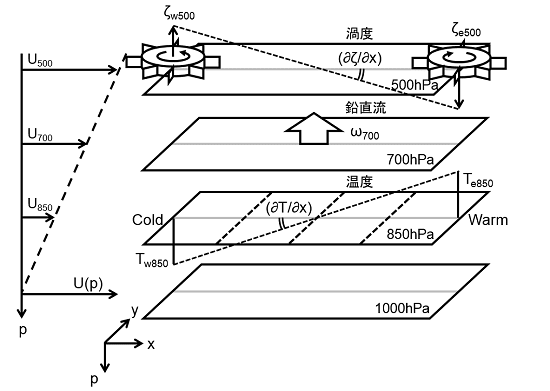
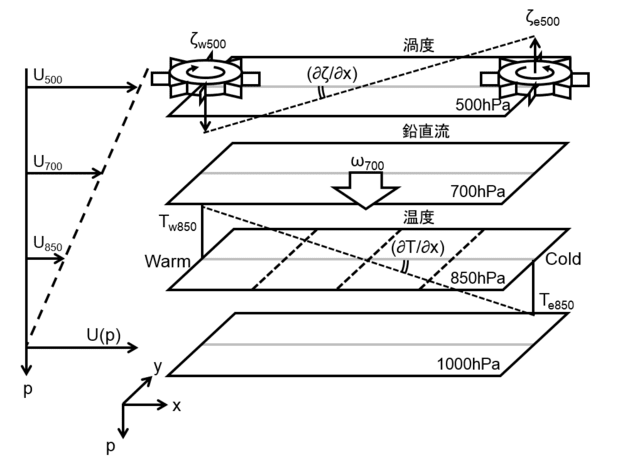
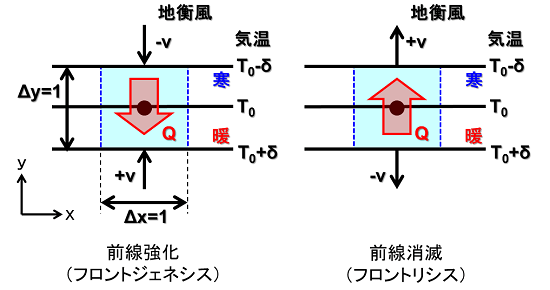
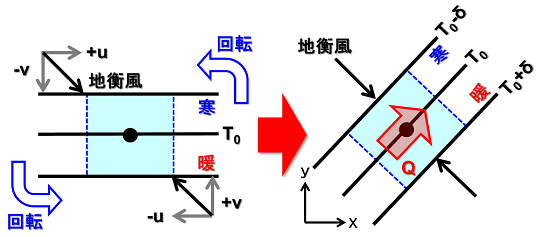
　特に、6月下旬は「太平洋高気圧」の勢力が特に強く、その勢いで梅雨前線も押し上げられてしまったようです。その背景について簡単な模式図を描いてみました。

　ポイントを簡単に書くと・・・

(1)ラニーニャ現象の影響で熱帯域の活発な対流が西側（フィリピン付近）にシフト。

(2)この対流の上空では顕著な発散場となるため、その北側を流れる偏西風がさらに北にシフト。

(3)偏西風が大きく蛇行して持続し（シルクロードパターン）、太平洋高気圧も西側に勢力拡大。

(4)正のＰＪパターン（フィリピン付近で対流が活発になり、日本付近の高気圧が強化）が成立。

(5)太平洋高気圧に押し上げられて、梅雨前線の北上が進み「梅雨明け」。

　このような背景で一先ず「梅雨明け」は発表されましたが、この後「梅雨の戻り」の可能性も予想されております。

（９月２日・追記）
９月１日、気象庁から梅雨入り梅雨明けの確定値が発表されました。
この結果、北陸地方・東北南部は共に「特定できない」に改められました。
https://www.data.jma.go.jp/cpd/baiu/index.html
６月下旬のケースは「梅雨明け」から「梅雨の中休み」の位置付けに変わったようです。

梅雨なのに…猛暑日

　今日(6/24)の新潟県内は、厳しい暑さに見舞われました。最高気温35℃以上を観測した地点を挙げてみますと・・・

・十日町：37.1
・大　潟：37.0
・小　出：36.9
・糸魚川：36.8
・高　田：36.7
・安　塚：36.5
・柏　崎：36.1
・長　岡：35.8
・湯　沢：35.4
・津　南：35.2
・三　条：35.1
・守　門：35.0

　正午時点の新潟県内の気温分布を見てみますと、上・中・下越の広い範囲で30℃を超えており、特に上越地方を中心に35℃を超えている地域が見られました。

　今日は日本海の低気圧や前線に向かって、太平洋高気圧の縁辺から顕著な暖気が流れ込んでいました。上空では1500m付近で18℃以上の暖気となっており、これは地上で30℃以上の目安でもあります。

　さらに、暖気の流れが山を乗り越える際の「フェーン現象」の影響も加わったため、真夏日を超えて猛暑日となる地点が現れました。それにしても、この時期にしては太平洋高気圧の勢力が強いように見えます。

　そういえば、まだラニーニャ現象が継続しているんですね・・・。

４種類の線状降水帯

　暦も６月に入り、梅雨前線の季節が近づいてきました。豪雨などの大雨に伴う被害が未然に防止されることを願って止みません。

　梅雨の時期はやはり「大雨」が気になります。集中豪雨のような大雨において重要な要因は、下層約１ｋｍまでの範囲内に含まれる水蒸気量です。また、大雨がもたらされた結果、その上空３ｋｍ程度の高さで湿舌が形成されます。

　さて、暖かく湿った空気が流れ込む等の要因で、大気の状態が非常に不安定になると、活発な対流が起こりやすくなります。このような場において、地形の影響等から誘発された上昇気流に伴って積乱雲が発生します。

　そして、様々な条件が重なると、積乱雲が列を成すような線状の激しい降水域（線状降水帯）が形成されます。今回は、線状降水帯の主な４つのパターンについて簡単なイメージを描いてみました。

(1) バックビルディング型

　下層の風と中層の風の向きが同じ場合、発生した積乱雲は中層の風に伴って風下側に移動します。そして、この背後には新たな積乱雲が発生します。

　このように同じ場所（後方）で積乱雲が次々に発生するパターンを「バックビルディング型」と言います。なお、バックビルディング型の線状降水帯については、過去にこちらの記事にも書きました。

(2) バックアンドサイドビルディング型

　下層の風と中層の風の向きが直向する場合、発生した積乱雲は中層の風に伴って風下側に移動します。ただ、下層の風が側方から加わるので、積乱雲の移動方向は少しずつ斜めに傾いていきます。そして、この積乱雲の背後や側方で新たな積乱雲が発生します。

　このように後方に加えて側方でも積乱雲が次々に発生するパターンを「バックアンドサイドビルディング型」と言います。上から見ると、雲や雨の領域は細長い三角形（ニンジン型）を形成しています。（中層の風の）風下側を頂点とし、風下に向かって横幅が広がるためです。

(3) スコールライン型

　下層の風と中層の風の向きが逆向きの場合、両者のぶつかり合う領域（収束帯）で上昇気流を生じます。この上昇気流に伴って積乱雲が発達するため、収束線（収束帯）に沿って幾つもの積乱雲が列を成すような形となります。このようなパターンを「スコールライン型」と言います。

(4) 破線型

　局地前線上に暖かく湿った空気が流入することで、前線上に積乱雲が発生します。もともとは、前線上に個々の積乱雲が生じるため、破線を描くような形となります。これらの積乱雲の発達に伴い、その領域が広がることで線状の降水帯となります。

　日本で多く見られるのは、「バックビルディング型」と「破線型」と言われています。

　※以上、４つのパターンについて紹介しましたが、実際の雲列を取り巻く風の流れはとても複雑です。その詳しい立体構造については、この記事では割愛しています。

オメガ方程式のイメージ

　気象予報士試験の勉強では必ず登場する「オメガ方程式」。その姿は見る者を圧倒します。

　少し解りやすくするために、次の２つの式を適用すると

　このように書き直すことができます。

　鉛直運動（鉛直流の分布）は「渦度移流の鉛直シア」と「温度移流」によって生じる、という意味です。また、上の式には書いておりませんが、「非断熱効果」を加えることもあります。

　数式自体が長く、複雑な形をしているので、その意味するイメージを描きにくいのが特徴です。試験対策としては、「鉛直流」の要因を考える際は「渦度移流の鉛直シア」「温度移流」あとは「非断熱効果」に着目する、と言うことを押さえておけばよいでしょう（実際、私がそうでした）。

　この記事では、「ごく簡単な条件」を想定することで、この複雑・難解な「オメガ方程式」のイメージを読み解いていきます。

　例えば、次のような場を考えてみましょう。x軸は東西方向、y軸は南北方向を表します。ここで、擾乱はy軸,p軸方向に一様とし、鉛直シアを持つ西風の一般流U(p)の場に重なるものと仮定します。

　今回は４つの等圧面(500,700,850,1000hPa)に着目します。
　想定する領域の長さをL_xとし、500hPa面は渦度ζ_w500（西端）とζ_e500（東端）、700hPa面は鉛直流ω₇₀₀（中央）、そして850hPa面は温度Ｔ_w850（西端）とＴ_e850（東端）とします。また、一般流として等圧面毎にＵ₅₀₀、Ｕ₇₀₀、Ｕ₈₅₀、Ｕ₁₀₀₀とします。これらは一様に西風とします（但し、上空ほど速度が増す）。

　つまり、「500hPa面と1000hPa面の間の渦度移流の鉛直シア」および「850hPa面の温度移流」から「700hPa面の鉛直流」が決まることを考えています。FAX天気図のイメージです。

　擾乱はy軸,p軸方向に一様と仮定したので、これらの物理量は「x軸方向のみ」を考えます。

　ここで、解ωの関数形について、次のような三角関数で表すことができると仮定します。

　続いて、微分演算子、一般流の鉛直シア、1000hPa面の一般流を次のように近似します。

　以上を「x軸方向のみ」のオメガ方程式に適用すると、次のような式が得られます。

　こうして簡単な代数方程式の形に帰着しました。あとは右辺の各項について見てみましょう。

右辺第１項について
・ζ_e500＜ζ_w500　⇒　(-ω₇₀₀)＞0 の側に作用する（上昇流）
・ζ_e500＞ζ_w500　⇒　(-ω₇₀₀)＜0 の側に作用する（下降流）

右辺第２項について
・T_e850＞T_w850　⇒　(-ω₇₀₀)＞0 の側に作用する（上昇流）
・T_e850＜T_w850　⇒　(-ω₇₀₀)＜0 の側に作用する（下降流）

　このように、渦度や温度の「移流」が「傾き」の形で表現されるので、イメージがつかみやすくなります。
　
　さて、上昇流となる場合のイメージ図は既出ですので、下降流となる場合のイメージ図も掲載しておきましょう。

　ちなみに、Ｑベクトルを用いると、オメガ方程式は次のように書き表されます。

　とってもシンプルになりました。

水平温度場の変化と鉛直循環を結ぶＱベクトル

　１か月ほど前の記事「前線形成と鉛直循環の励起」では、水平面上において地衡風による温度場（温位場）の変化が生じると、二次的な鉛直循環が励起されることを紹介しました。

　そして、この鉛直循環は、地衡風による温度場（温位場）の変化によって生じた温度風バランスの崩れを解消する（基に戻す）働きを持っていました。

　水平面で地衡風の収束が生じ、フロントジェネシス（前線強化・温位傾度が増大）を生じると、鉛直面ではフロントリシス（前線消滅・温位傾度が減少）の二次循環を生じます。

　一方、水平面で地衡風の発散が生じ、フロントリシスを生じると、鉛直面ではフロントジェネシスの二次循環を生じます。

　このような「水平面上の温度場（温位場）の変化」と「鉛直循環の発生」を関連付ける指標として「Ｑベクトル」が用いられます。Ｑベクトルの定義は、主に次の式が用いられます。

　この式を、水平面上におけるフロントジェネシスとフロントリシスの各ケースについて適用してみます。まずは、各ケースについて、ごく簡単な条件を設定してみましょう。

　水平面（ｘ－ｙ平面）上に等温線を３本引いています。つまり、ｙ方向に温度傾度を生じています。ここで、同じくｙ方向の地衡風を仮定します。

　いま、対象領域（水色の正方形）の中心「●」におけるＱベクトルを考えます。簡単のため、正方形のｘ方向、ｙ方向の距離（Δｘ、Δｙ）は単位長さ（＝１）とします。

　フロントジェネシス（左側）では、ｙ方向の地衡風（上・－ｖ，下・＋ｖ）が対象領域の中心に向かうように収束しています。このため、温度傾度が増大する（等温線の間隔が狭まる）ように推移します。

　フロントリシス（右側）では、ｙ方向の地衡風（上・＋ｖ，下・－ｖ）が対象領域の中心から離れるように発散しています。このため、温度傾度が減少する（等温線の間隔が広がる）ように推移します。

　各ケースで仮定した条件をＱベクトルの定義式に適用します。

　このように、各ケースにおけるＱベクトルが得られました。式だけを見ても判りにくいので、先ほどの図にＱベクトルを重ねて書いてみます。Ｑベクトルは赤で示しました。

　フロントジェネシスの場合（左側）、Ｑベクトルはｙ軸負の向きとなりました。等温線に垂直で、暖気側を指しています。

　フロントリシスの場合（右側）、Ｑベクトルはｙ軸正の向きとなりました。等温線に垂直で、寒気側を指しています。

　それで、Ｑベクトルと鉛直循環の間にはどのような関係があるのでしょうか。冒頭の図に倣って、立体的に考えてみましょう。

　冒頭の図をベースにＱベクトルを重ねてみました。この結果、Ｑベクトルの指す側で上昇流、反対側で下降流となるような鉛直循環が励起されることが判ります。


　ここまでは、水平面上における等温線と地衡風が垂直に交わる場合を考えてきました。続いては、等温線と地衡風が互いに斜めの場合を考えてみましょう。

　今回は一例として、斜めの地衡風に伴って温度場自体が（等温線の間隔を保ちながら）回転するような場合を想定してみます。

　上の図で仮定した条件をＱベクトルの定義式に適用します。

　得られたＱベクトルを、図に重ねて書いてみます。これまでと同様にＱベクトルは赤で示しました。

　Ｑベクトルはｘ軸、ｙ軸共に正の向きとなりました。等温線に平行な向きを指しています。

　さて、一般的なＱベクトルと鉛直流の関係については、Ｑベクトルを用いたオメガ方程式で説明されます。この辺の話はまたの機会に。