先の冬は暖冬・少雪の傾向が顕著に表れました。一方、2年前はこれとは正反対の大雪に見舞われました。そこで、先の冬(暖冬・少雪)と2年前の冬(寒冬・大雪)の新潟県内の降雪量を比較してみました。
冬の期間は概ね12月から翌年3月ですが、ここでは簡単のため1月から2月の2か月間の積算降雪量を比較することにします。
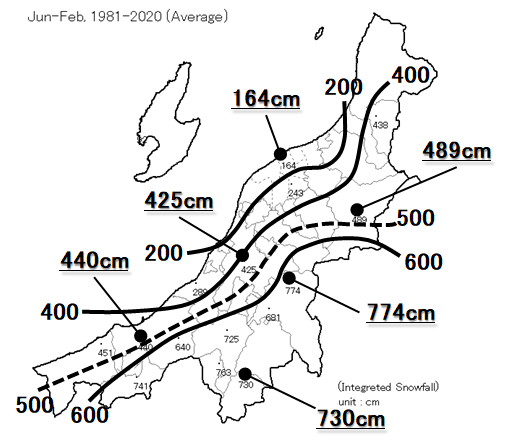
まずは「平年値の分布」を描いてみました。等値線は200,400,500,600cmで引いています。また、主な観測地点の積算降雪量を個別に表記しています。
平野部では概ね200~500cm程度ですが、沿岸部では200cmを下回る所もあります(新潟市では164cm)。一方、山間部では500~700cm程度で、中には700cmを超える所もありました。
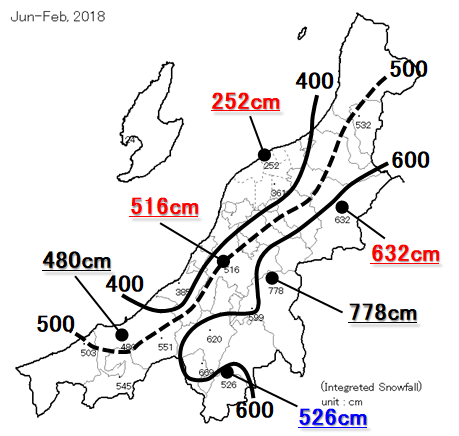
続いては、大雪となった2018年1月-2月の場合です。平野部では沿岸部の新潟で252cmと平年値を大きく上回り、概ね300~600cm近くに達していました。降雪量を赤字で示した地点は、降雪量が平年値を大きく上回った所です。
このシーズンは、日本海寒帯気団収束帯(JPCZ)が下越地方(新潟県北部)の平野部に向かって延びる事例に数多く遭遇しました。正直、天気図を見るたびにウンザリしていたような気がします。このJPCZの走向に伴い、雪雲が山沿いの地域よりも下越地方の平野部に流れ込みやすく、この付近を中心に大雪となる傾向が見られました。
また、降雪量が平年値を下回った所は青字で示しました。雪雲が下越地方の平野部に流れ込みやすかったため、上越・中越地方(新潟県南部・中部)の山沿いの地域では返って降雪量が少なくなりました。

そして、この前の2020年1月-2月の場合です。降雪量自体は全体的に山沿い中心の分布となっています。それにしても、降雪量が少ない。等値線が足りないので、100cmの線を追加で引きました。平野部では100cmに満たなかったのです。また、山沿いの地域でも400cmを超えたのは一部の範囲だけでした。
天気図を見ていても、確かに冬型の気圧配置にはなるものの、「上空の寒気」の気温が普段よりも高めだな、と感じることが多々ありました。これは正の北極振動やインド洋ダイポールモードの影響が重なったことが主な要因です。実に興味深いケースです。
冬の期間は概ね12月から翌年3月ですが、ここでは簡単のため1月から2月の2か月間の積算降雪量を比較することにします。

平年値の降雪量分布(1月・2月)
まずは「平年値の分布」を描いてみました。等値線は200,400,500,600cmで引いています。また、主な観測地点の積算降雪量を個別に表記しています。
平野部では概ね200~500cm程度ですが、沿岸部では200cmを下回る所もあります(新潟市では164cm)。一方、山間部では500~700cm程度で、中には700cmを超える所もありました。

2018年1月-2月の降雪量分布(寒冬・大雪の場合)
続いては、大雪となった2018年1月-2月の場合です。平野部では沿岸部の新潟で252cmと平年値を大きく上回り、概ね300~600cm近くに達していました。降雪量を赤字で示した地点は、降雪量が平年値を大きく上回った所です。
このシーズンは、日本海寒帯気団収束帯(JPCZ)が下越地方(新潟県北部)の平野部に向かって延びる事例に数多く遭遇しました。正直、天気図を見るたびにウンザリしていたような気がします。このJPCZの走向に伴い、雪雲が山沿いの地域よりも下越地方の平野部に流れ込みやすく、この付近を中心に大雪となる傾向が見られました。
また、降雪量が平年値を下回った所は青字で示しました。雪雲が下越地方の平野部に流れ込みやすかったため、上越・中越地方(新潟県南部・中部)の山沿いの地域では返って降雪量が少なくなりました。

2020年1月-2月の降雪量分布(暖冬・少雪の場合)
そして、この前の2020年1月-2月の場合です。降雪量自体は全体的に山沿い中心の分布となっています。それにしても、降雪量が少ない。等値線が足りないので、100cmの線を追加で引きました。平野部では100cmに満たなかったのです。また、山沿いの地域でも400cmを超えたのは一部の範囲だけでした。
天気図を見ていても、確かに冬型の気圧配置にはなるものの、「上空の寒気」の気温が普段よりも高めだな、と感じることが多々ありました。これは正の北極振動やインド洋ダイポールモードの影響が重なったことが主な要因です。実に興味深いケースです。