4年前の記事「
角運動量保存の法則」(2020-08-26)で、「気が向いたらまたの機会に…」と記していた「渦位」について、今回は書いていきます。
さて、気象の世界では「渦位」とは「絶対渦度と安定度の積」と表記されることが多いようです。しかし、それだけでは直感的なイメージがなかなか浮かび上がりません。
そこで今回は、「渦位」とは「角運動量と(絶対)渦度の性質を合体した物理量」との観点からイメージを描いていこうと思います。まずは「角運動量」と「渦度」のイメージをそれぞれ再確認し、その後で「渦位」のイメージを組み立てていきます。
1.角運動量のイメージを再確認
過去の記事「
角運動量保存の法則」(2020-08-26)も併せて御参照下さい。
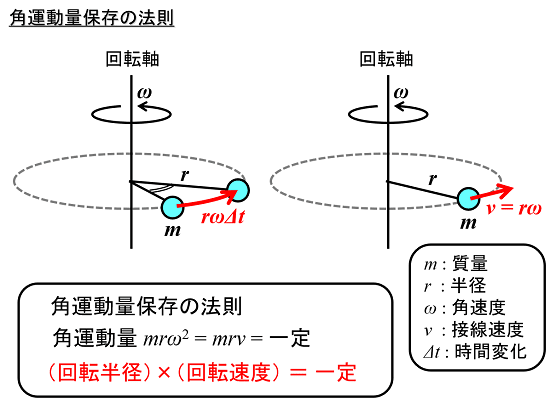
回転半径と回転速度の積が一定になる原理を「角運動量保存の法則」と言います。
いま、回転軸の周りを半径r[m]、角速度ω[rad/s]で円運動する質量m[kg]の質点を考えます。この時、質点mの速度v[m/s]はv=rωで表されます。
ここで運動量は「(質量)×(速度)=mv=mrω」で定義されます。回転運動の場合は新たに、角運動量「(質量)×(半径)×(速度)=mrv=mrω
2」という物理量を考えます。
この角運動量が保存される「(角運動量)=(質量)×(半径)×(速度)=(一定)」というのが「角運動量保存の法則」です。
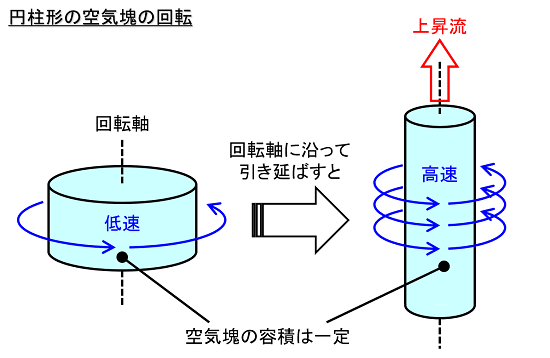
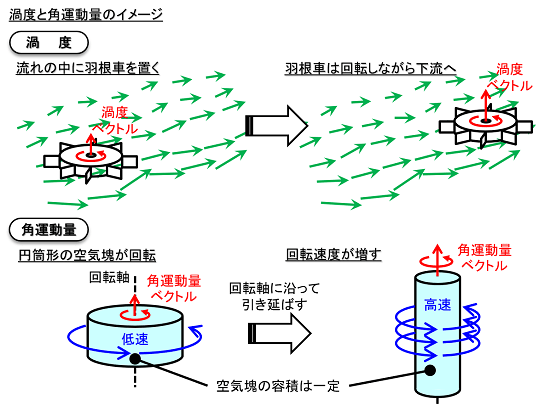
例えば、円柱形の空気塊が回転している時に、周囲の上昇流に伴って空気塊が鉛直に引き延ばされると、その回転の勢いが増します。
上の図では、左側の状態では回転半径が大きく、ゆっくりと回転しています。この空気塊が、何らかの理由で生じた上昇流によって、鉛直方向に引き延ばされると、右側のように細長くなってしまいます。
つまり、容積は一定のまま、回転半径は小さくなります。先の「角運動量保存の法則」の考え方に基づけば、半径が小さくなる分、回転速度が増すことになります。
空気塊を鉛直に引き延ばすような上昇流は、積乱雲による場合もあれば、日射による地表面の加熱の場合もあります。
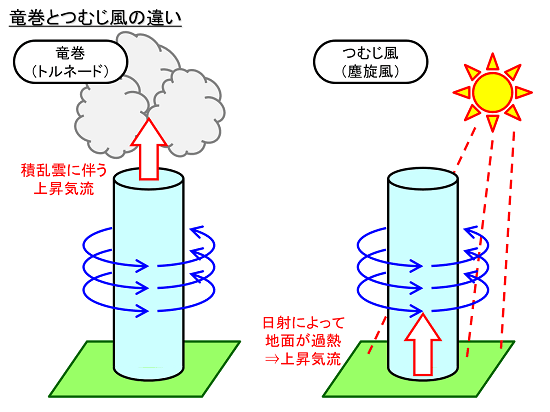
竜巻は「積乱雲に伴う活発な上昇流」によって発生するものです。この上昇流によって、空気塊は鉛直方向に引き延ばされることで、強い渦が形成されます。
一方、つむじ風(塵旋風)は「地面が日射によって加熱されることで生じる上昇流」によって発生します。この上昇流によって、空気塊は鉛直方向に引き延ばされます。
両者は一見すると形が似ていますが、上昇流の要因は異なります。
2.渦度のイメージを再確認
渦度については、こちらの過去記事も併せて御参照下さい。
絶対渦度と相対渦度のイメージ(2018-01-18)
ベータ効果のイメージ(2018-01-19)
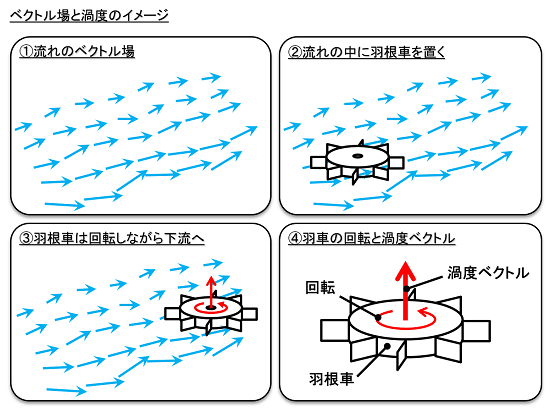
流れ場の中に「羽根車」を置くと、羽根車はクルクルと回転しながら下流へ移動します。この回転の指標が「渦度」であり、回転軸上の「ベクトル量」として表されます。流れ場が水平面上にある場合、渦度ベクトルは鉛直方向に生じます。この渦度(鉛直成分)の大きさをζ、水平面上のベクトル場を(u,v)と表記すると、「ζ=(∂v/∂x)-(∂u/∂y)」の関係が成り立ちます。
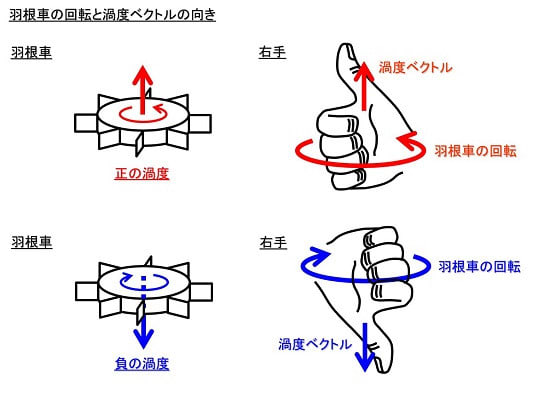
羽根車の回転と渦度の向きの関係は「右手の法則」で表すこともできます。右手の4本の指を回転の向きとすると、親指が渦度ベクトルの向きに対応します。正の渦度は「反時計回り」、負の渦度は「時計回り」の回転です。
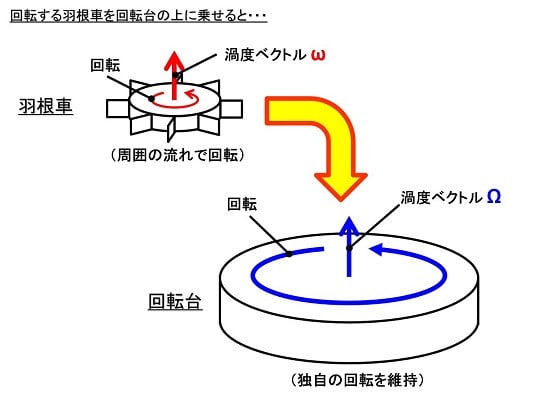
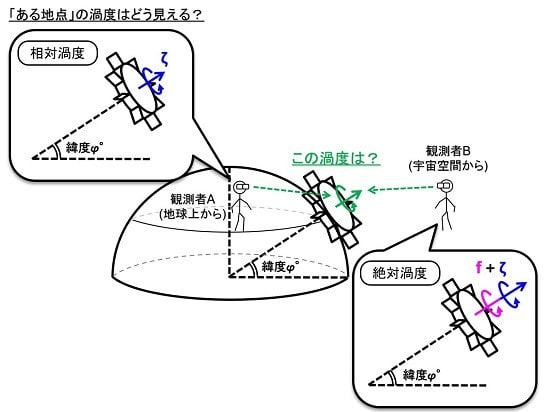
続いて、既に回転している羽根車(渦度ω)を「そっくりそのまま」別の回転状態にある回転台(渦度Ω)の上に乗せてみます。この時、羽根車の回転に伴う渦度は、回転台の上から見た場合と回転台の外から見た場合では、見え方が違ってきます。
ここで、2人の観測者AとBに登場してもらいます。一緒に回転台に乗るAから見た羽根車の渦度は「ω」のままです。一方、回転台の外のBから見ると、渦度は「Ω+ω」となります。前者を「相対渦度」、後者を「絶対渦度」と言います。
この「絶対渦度」と「相対渦度」の概念は、地球を取り巻く大気の流れに伴って生じる渦度を考える際に重要になります。「地球上にいる人」が「地球上で生じる渦度」を見た場合は「相対渦度」となる一方、「宇宙空間のある地点に固定された場所」から「地球上で生じる渦度」を見た場合は「絶対渦度」という事です。
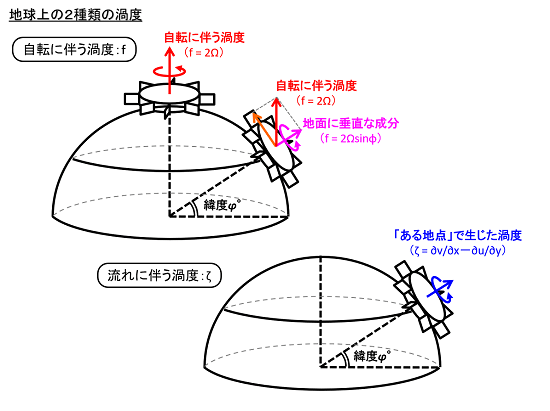
いま、自転する地球は「回転台」(渦度f=2Ω)に相当します。fの値は緯度φ°に応じて変化し、f=2Ωsinφです。
さらに大気の流れに伴い、「ある地点」で別の渦度が生じると、これは「羽根車」(渦度ζ)に相当します。この時、羽根車の渦度は地球上のAから見ると「ζ」、宇宙空間のBから見ると「f+ζ」となります。
3.渦位のイメージを構築
以上の内容を踏まえて、渦位のイメージを組み立てていきます。
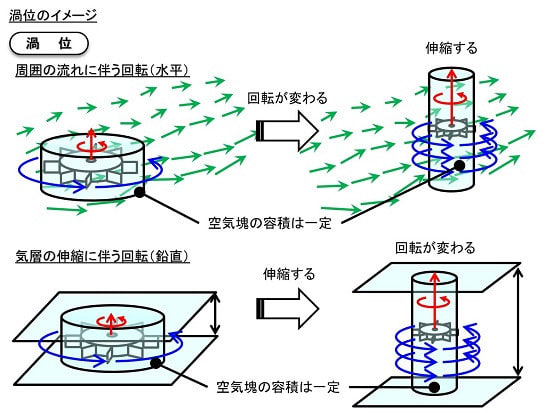
流れ場の中に「羽根車」を置くと、羽根車は回転しながら下流へ移動します。この回転の指標が「渦度」です。また「角運動量保存則」によれば、回転する円柱形の空気塊が鉛直に引き延ばされると、その回転の勢いが増します。これらの概念を一つにまとめると「渦位」のイメージが浮かび上がります。
流体要素の「回転」と「伸縮」は表裏一体です。流れ場の面を水平面とすると、水平面の回転が変われば鉛直方向にも伸縮し、また鉛直方向に伸縮すれば水平面の回転も変わります。このように「互いのバランスを取るように」流体の挙動は形作られます。ここで、回転の度合いは「渦度」に相当し、伸縮の度合いは「角運動量」に相当します。
ここで「空気塊の上端と下端を挟む平面が何なのか」によって、渦位を表現する式が変わります。例えば、浅水系の順圧大気であれば「等圧面」が考えられます。また、傾圧大気の場合は「等温位面」が多く用いられます。この上下の面の間隔が変化することで、流体要素が引き延ばされたり、縮められることで、回転の勢いも変化するわけです。
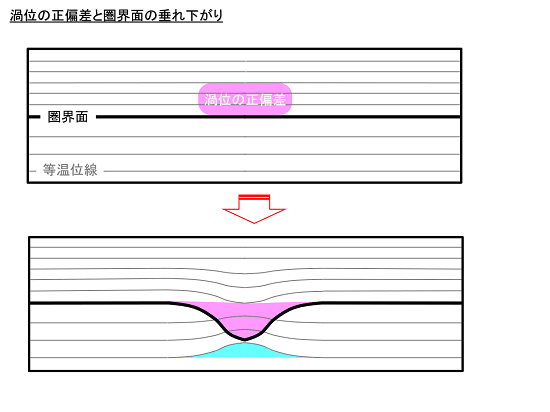
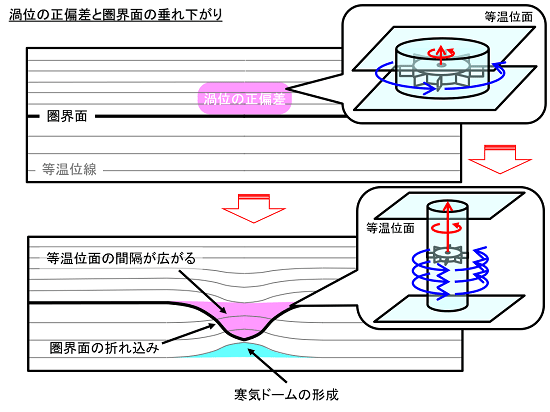
ここからは、傾圧大気の場合を考えてみます。簡単のため、初期状態では(上図の上段のように)圏界面と等温位面は水平であると考えます。また、温位の分布については「下層で低く、上層で高い」ものとし、温位の鉛直傾度は対流圏より成層圏で大きいものとします。
ここで、上下を等温位面で挟まれた空気塊の渦位を考えた場合、圏界面付近で渦位の正偏差を生じると、その付近では(上図の下段のように)圏界面が次第に垂れ下がります。これに伴って、等温位面にも変化が生じます。
ここで、これまでのイメージを描き加えてみましょう。圏界面が垂れ下がった領域では、等温位面の間隔が広がるため、空気塊が鉛直に引き延ばされます。このため、正の回転が強まります。渦位の正偏差の成せる業ですね。
また、対流圏上部の等温位面が一部、圏界面の上方に取り込まれるため、部分的に等温位面が盛り上がります。従って、この付近では周囲よりも温位が低くなります。この影響は下層にも及ぶため、下層で寒気ドームを形成します。
今度は視点を変えて、等圧面と温度場の観点から見てみましょう。
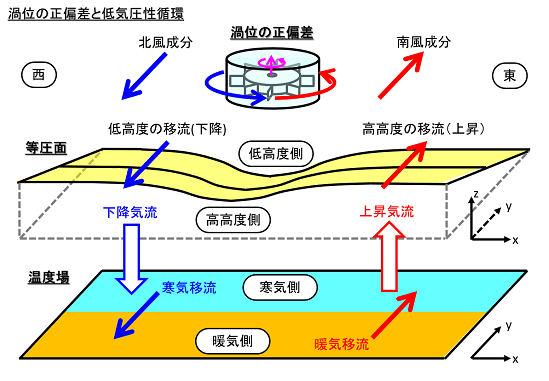
渦位の正偏差と言うことは「正の回転(低気圧性循環)」となるので、その西側では北風成分、東側では南風成分が卓越することになります。ここで、北半球の等圧面の高度分布を考えてみると「南側で高く、北側で低い」傾向があります。
つまり、渦位の正偏差から見て、西側では北風成分に伴い「低高度の移流(高度が下がる)」、東側では南風成分に伴い「高高度の移流(高度が上がる)」を生じます。従って、西側では下降気流、東側では上昇気流の場の構造が浮かび上がります。
さらに、北半球の等圧面の温度分布を考えてみると「南側で高く、北側で低い」傾向があります。つまり、渦位の正偏差から見て、西側では北風成分に伴い「寒気移流」、東側では南風成分に伴い「暖気移流」を生じます。
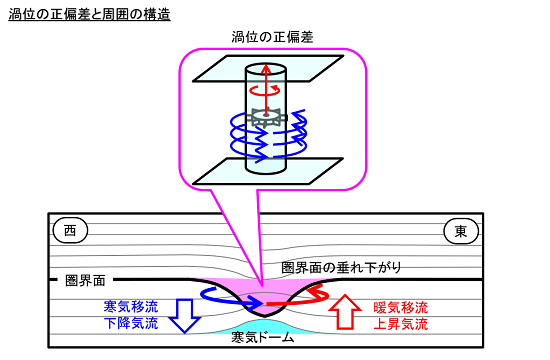
以上をまとめると、渦位の正偏差の周囲では低気圧性循環が卓越し、その下層では寒気ドームが形成されます。また、西側では寒気移流の下降流場、東側では暖気移流の上昇流場が顕著になる構造が描けるのです。
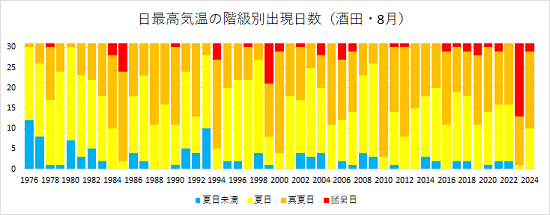
さて、「絶対渦度」は「非発散・断熱・摩擦無し」の条件で保存されるのに対し、「渦位」は「断熱・摩擦無し」の条件で保存されます。収束・発散があっても保存されるという点で、大気の流れを追跡するのに都合が良いという利点があります。
対流圏中層(500hPa面)では、他の高度より収束・発散が小さいため「相対渦度」が用いられます。その一方で、対流圏界面付近では「渦位」が用いられます。
低気圧の発達や上空の寒冷渦などの成因を考察する上で、圏界面付近の渦位の偏差を把握することも重要であることを述べて、この記事の締め括りとしましょう。