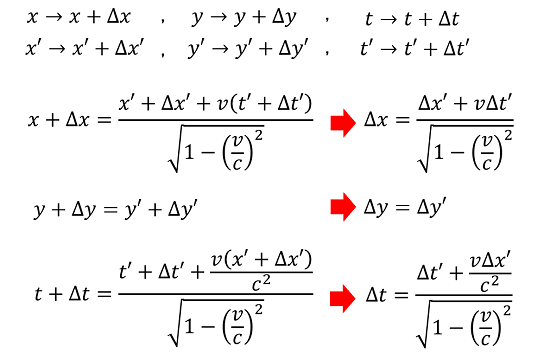【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897846329.html
前回の記事では「ローレンツ変換」を導入しました。今回はその続編として「エネルギーと質量の等価性」を導いてみます。
ここでも、前回と同様に2つの慣性系としてK系とK'系を導入し、それぞれに観測者A、Bが存在すると考えます。また、K系は静止する一方、K'系は(K系に対して)一定の速度vで運動する状況を想定しています。
【等速運動する慣性系における物体の衝突】
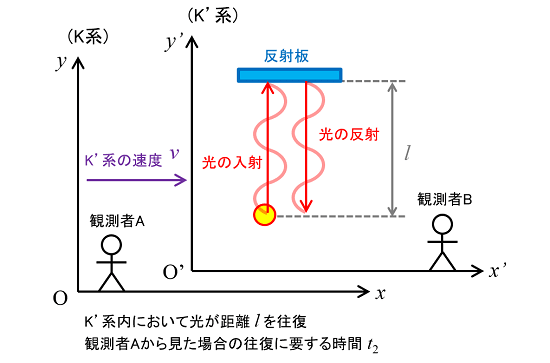
今回は、等速運動する慣性系(K'系)の中で2つの物体を衝突させてみます。この2つの物体は同じ質量を持っており、互いに同じ速さ(向きは逆向き)で等速運動して衝突に至ります。

この場合、K'系の観測者BとK系の観測者Aでは、現象の見え方(認識)が異なります。まず、観測者Bから見ると「同じ質量m'の物体が、同じ速さu'で逆向きに運動して正面衝突し、衝突直後は静止状態に至る」と認識します。
一方、観測者Aから見ると「物体1と2は互いに同じ向きに、異なる速さu1,u2で等速運動しており(u1>u2)、物体1が物体2に追いつくように衝突し、衝突直後は(慣性系K'と同じ)速度vで運動する」と認識します。
また、観測者Aから見ると、ローレンツ変換によってK'系内の時間と空間が変化しているので、2つの物体の質量m1,m2についても「互いに等しい」と認識できるとは限りません。
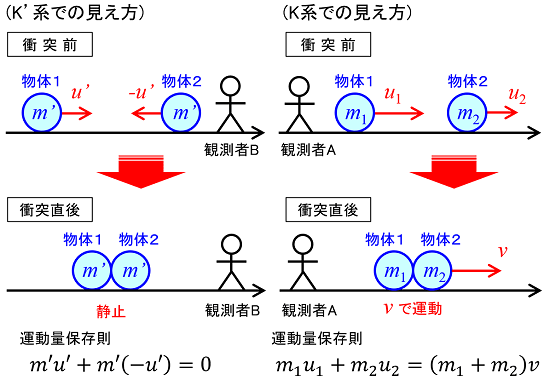
そこで、K系の観測者Aの視点で、K'系内の2物体の運動量保存則、および各物体の速度のローレンツ変換の式と立て、2物体の質量比(m1/m2)を導きます。
本来、2つの物体と同じ慣性系に存在する観測者(この場合はB)から見れば、質量比は「もちろん1」となるのですが、異なる慣性系の観測者(この場合はA)から見ると「必ずしも1とは限らない」と考えるのです。

ここで、この質量比(m1/m2)2の式は、運動量保存則とローレンツ変換の式から「u'とvを消去する」ことで導かれるのですが(教科書には「この記述」しかなかった)、このやり方には「コツ」があります。当初、独力ではなかなか導けなかったので、ネットで調べて漸くそのテクニックを見つけました。

(※予め「1-u12/c2」と「1-u22/c2」を計算しておいて、後からまとめて代入するのです。)
【相対論的質量】
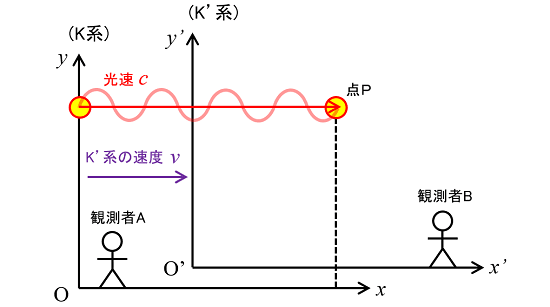
続いて、K系とK'系のそれぞれに物体を置いた場合を考えてみます。今度は、物体1はK'系において静止状態にあり、物体2はK系において静止状態にある状況を考えます。
この場合、観測者Bから見ると物体1は静止状態として認識されます。一方、観測者Aから見ると物体1は(K'系と同じ速度)vで等速運動していると認識されます。

さて、そもそもの前提として、物体1と物体2は同じ慣性系においては同じ質量を持っています。そこで、物体2を物体の本来の質量m0、物体1をK'系において変化したかも知れない質量mと考えて、質量比(m1/m2)を求めてみます。

この結果、K'系内における質量はmは、本来の質量m0のγ倍に変化していることが判りました。この変化した質量mを「相対論的質量」と言います。
【相対論的力学】
古典力学における「運動量」は質量と速度の積で定義されます。また、「ニュートンの運動方程式」は、「運動量の時間微分が外力に等しい」という形で表されます。
これを踏まえて、相対論的質量と速度の積を「相対論的運動量」と言います。また、「相対論的運動量の時間微分が外力に等しい」という形で表される方程式を「相対論的運動方程式」と言います(次の式では速度と外力をベクトルで表記しています)。

ここで、エネルギーの変化は外力による仕事によってもたらされると考えると、エネルギーの微小変化(dE)は微小仕事(F・dr)で表されます。後はひたすら数学の問題です。

両辺を速度0からvまで積分すると、エネルギーの変化と質量の変化の関係(エネルギーと質量の等価性)が導かれます。

ここで「右辺」の積分には、これまたちょっとした「コツ」が必要となります。こちらもネットで調べて漸くそのテクニックを見つけました。
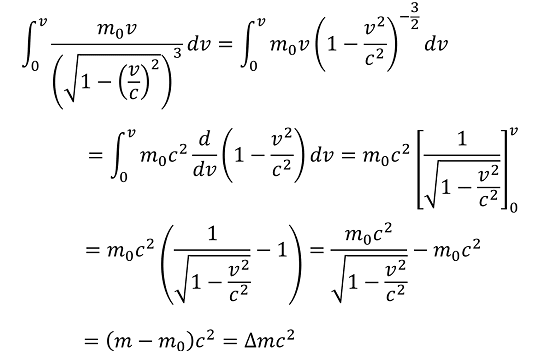
(※要は「(1-v2/c2)-3/2=(d/dv)(1-v2/c2)」を発想できるかどうかがポイントです。)

https://ameblo.jp/qq-otenki-s/entry-12897846329.html
前回の記事では「ローレンツ変換」を導入しました。今回はその続編として「エネルギーと質量の等価性」を導いてみます。
ここでも、前回と同様に2つの慣性系としてK系とK'系を導入し、それぞれに観測者A、Bが存在すると考えます。また、K系は静止する一方、K'系は(K系に対して)一定の速度vで運動する状況を想定しています。
【等速運動する慣性系における物体の衝突】
今回は、等速運動する慣性系(K'系)の中で2つの物体を衝突させてみます。この2つの物体は同じ質量を持っており、互いに同じ速さ(向きは逆向き)で等速運動して衝突に至ります。

この場合、K'系の観測者BとK系の観測者Aでは、現象の見え方(認識)が異なります。まず、観測者Bから見ると「同じ質量m'の物体が、同じ速さu'で逆向きに運動して正面衝突し、衝突直後は静止状態に至る」と認識します。
一方、観測者Aから見ると「物体1と2は互いに同じ向きに、異なる速さu1,u2で等速運動しており(u1>u2)、物体1が物体2に追いつくように衝突し、衝突直後は(慣性系K'と同じ)速度vで運動する」と認識します。
また、観測者Aから見ると、ローレンツ変換によってK'系内の時間と空間が変化しているので、2つの物体の質量m1,m2についても「互いに等しい」と認識できるとは限りません。

そこで、K系の観測者Aの視点で、K'系内の2物体の運動量保存則、および各物体の速度のローレンツ変換の式と立て、2物体の質量比(m1/m2)を導きます。
本来、2つの物体と同じ慣性系に存在する観測者(この場合はB)から見れば、質量比は「もちろん1」となるのですが、異なる慣性系の観測者(この場合はA)から見ると「必ずしも1とは限らない」と考えるのです。

ここで、この質量比(m1/m2)2の式は、運動量保存則とローレンツ変換の式から「u'とvを消去する」ことで導かれるのですが(教科書には「この記述」しかなかった)、このやり方には「コツ」があります。当初、独力ではなかなか導けなかったので、ネットで調べて漸くそのテクニックを見つけました。

(※予め「1-u12/c2」と「1-u22/c2」を計算しておいて、後からまとめて代入するのです。)
【相対論的質量】
続いて、K系とK'系のそれぞれに物体を置いた場合を考えてみます。今度は、物体1はK'系において静止状態にあり、物体2はK系において静止状態にある状況を考えます。
この場合、観測者Bから見ると物体1は静止状態として認識されます。一方、観測者Aから見ると物体1は(K'系と同じ速度)vで等速運動していると認識されます。

さて、そもそもの前提として、物体1と物体2は同じ慣性系においては同じ質量を持っています。そこで、物体2を物体の本来の質量m0、物体1をK'系において変化したかも知れない質量mと考えて、質量比(m1/m2)を求めてみます。

この結果、K'系内における質量はmは、本来の質量m0のγ倍に変化していることが判りました。この変化した質量mを「相対論的質量」と言います。
【相対論的力学】
古典力学における「運動量」は質量と速度の積で定義されます。また、「ニュートンの運動方程式」は、「運動量の時間微分が外力に等しい」という形で表されます。
これを踏まえて、相対論的質量と速度の積を「相対論的運動量」と言います。また、「相対論的運動量の時間微分が外力に等しい」という形で表される方程式を「相対論的運動方程式」と言います(次の式では速度と外力をベクトルで表記しています)。

ここで、エネルギーの変化は外力による仕事によってもたらされると考えると、エネルギーの微小変化(dE)は微小仕事(F・dr)で表されます。後はひたすら数学の問題です。

両辺を速度0からvまで積分すると、エネルギーの変化と質量の変化の関係(エネルギーと質量の等価性)が導かれます。

ここで「右辺」の積分には、これまたちょっとした「コツ」が必要となります。こちらもネットで調べて漸くそのテクニックを見つけました。
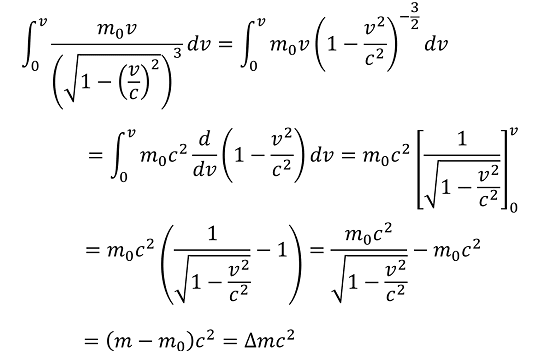
(※要は「(1-v2/c2)-3/2=(d/dv)(1-v2/c2)」を発想できるかどうかがポイントです。)