冬季降水量のニューロ・モデル解析

　天候デリバティブと並行して独自に研究を進めているのが、ニューラルネットワークを用いた降水域分布の解析です。もともと、情報工学におけるニューラルネットワークでは入力・出力共に「０と１からなる信号」を想定しています。

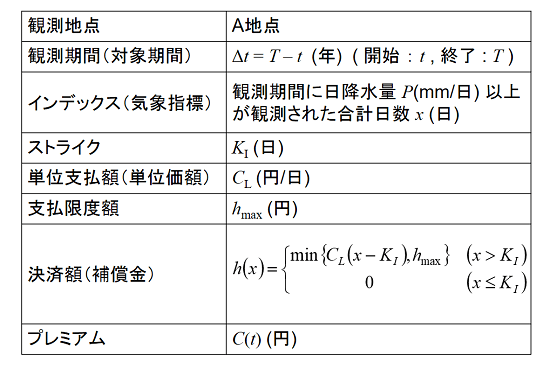
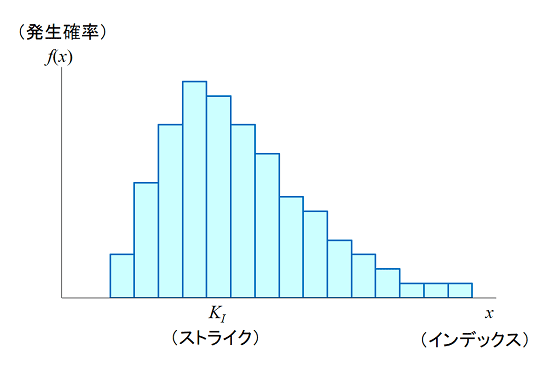
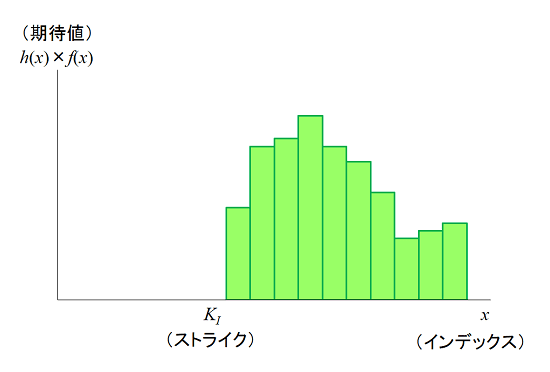
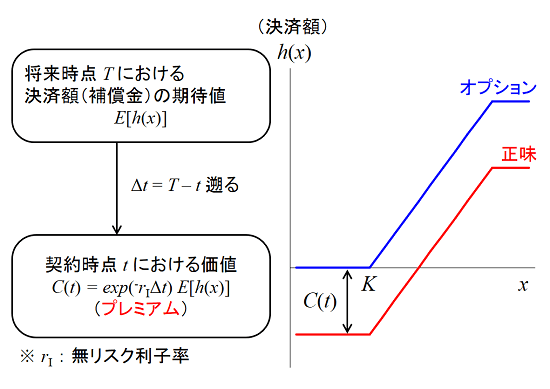
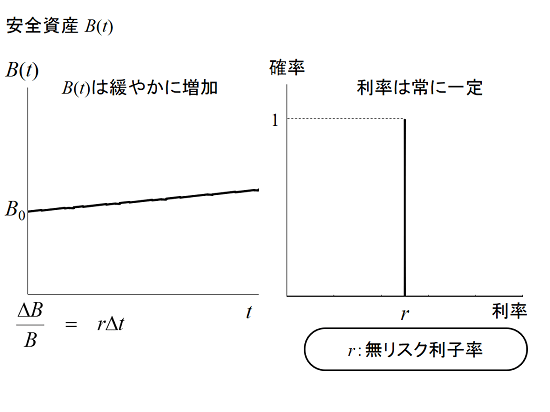
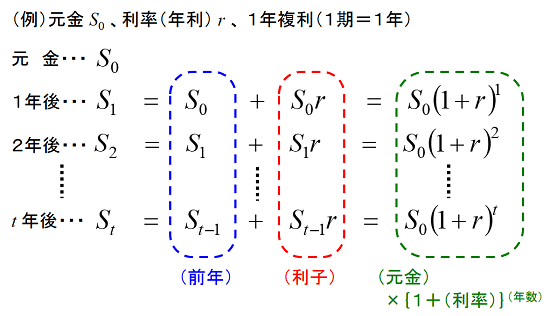
　しかし、気象のパラメータは連続的に変動するため（アナログ）、０か１か（デジタル）で表現する情報とは性格が異なります。このため、入力・出力のパラメータをどのように扱うか、などの課題がありました。約10年に渡る試行錯誤を経て、一つの成果を上げるに至りました。次の図は計算の概要です。

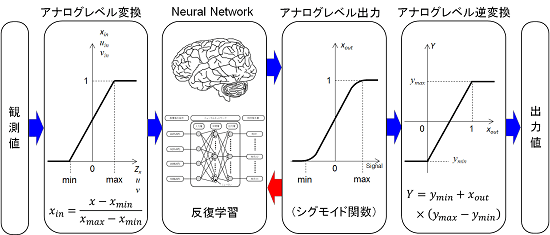
　今回は、降水量に相当する「相対降水量」の算出方法を変更して解析を試みました。今回の相対降水量は、平均レベルが０、平均より多い場合は正の値、平均よりも少ない場合は負の値となります。

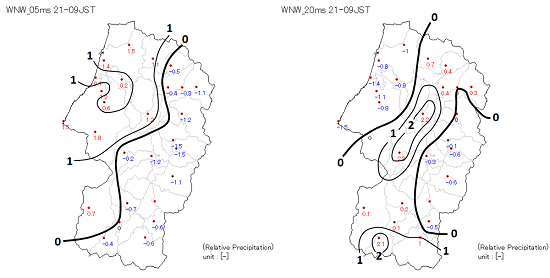
　こちらは山形県の場合です。左側は季節風の弱い場合の相対降水量の分布、右側は季節風が強い場合の相対降水量の分布です。

　相対降水量が０以上の領域を「降水域」として注目してみると、季節風が弱い場合は海側を中心に広がる一方、季節風が強くなるにつれて内陸側に進入する傾向が再現されています。この傾向は、３次元熱流体数値モデルによる山形県内の降雪域形成シミュレーションの結果と一致しています。

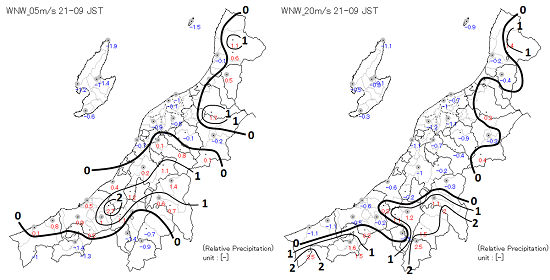
　続いてこちらは新潟県の場合です。左側は季節風の弱い場合の相対降水量の分布、右側は季節風が強い場合の相対降水量の分布です。季節風が弱い場合は平野部を中心に広がる一方、季節風が強くなるにつれて山間部中心に偏る傾向が再現されました。

金融工学の天候リスクへの応用 ～天候デリバティブ～

 天候デリバティブとは、将来の気象の変化に対して「保険」を掛けることにより、そのリスクをヘッジする手段です。これは、契約時に設定された一定の気象条件が実現した場合（指定された気象要素が閾値を超えたことが観測された場合）に、その観測値（閾値からの差分）に応じた補償金が支払われる「金融商品」です（※厳密には保険商品ではありません）。

 契約の際には、利用者は「保険の掛け金」に相当する「プレミアム」を保険会社等に支払います。このプレミアムは、将来における天候の影響とその発生確率に基づく期待値を基に算出されるため、将来における天候リスクの経済効果の指標と理解することもできます。そこで、ここでは簡単な契約プラン例を挙げて、プレミアムの算出について考えてみたいと思います。

 この例は、降水日数を指標とするコール・オプション取引です。

 インデックス（気象指標）には、観測期間中（Δｔ）に観測点（Ａ地点）で日降水量がＰmm以上を観測した日数（降水日数）の合計値ｘを用い、その値がＫ_I日（ストライク＝閾値）を超えると補償金が発生する仕様となっています。ここで、単位支払額はインデックス１日当たりＣ_L円、支払限度額はｈ_max円です。

 インデックスと補償金の関係を表すと、次のグラフのようになります。

 インデックスｘがストライク（Ｋ_I日）に達していなければ、補償金ｈ(ｘ)は発生しません。しかし、インデックスがストライクを超える場合は、その超過分に応じて（１日当たりＣ_L円の割合で）補償金が増えて行きます。但し、最大補償はｈ_max円と定められています。

 過去の気象データを基に、観測期間中（Δｔ）に観測点（Ａ地点）における日降水量がＰmm以上を観測した日数ｘを集計し、横軸にインデックスｘ、縦軸にはインデックスの発生確率（過去の出現頻度）ｆ(ｘ)という形に書き直してみます。

 続いて、インデックスと発生する補償金の関係を考えてみます。

 上の２つのグラフを基に、インデックスｘと発生する補償金の期待値ｈ(ｘ)ｆ(ｘ)を求めてみます。

 補償金と出現確率の積の総和＝このグラフの面積が、天候リスクに伴う補償金の期待値となります。平均的に発生し得る補償金額に相当します。そして、この補償金はあくまで将来時点（満期）における価値なので、これを現在時点（契約時）の価値に換算します。この換算された金額を基にプレミアムが決まります。

 ここで、ｒ_Iは無リスク利子率、exp(－ｒ_IΔｔ)はディスカウント・ファクターです。

オプション取引とBlack-Scholesの公式

 オプションとは、将来の一定期間に、約束した金額で金融商品（金融資産）を売ったり、買ったりする事ができる「権利」です。

 例えば、『株Ａ（時価：１１０万円）を６か月後に、１００万円で購入するオプション（権利）を購入する』 事案を考えてみましょう。この時、株Ａのことを「原資産」、６か月後と言う時期のことを「満期」、１００万円という価格を「権利行使価格」または「ストライク」と言います。

 もし、満期・６か月後に原資産・Ａの株価が暴落して、時価５０万円になった場合、このオプションを「放棄」することで、損失を免れることができます。一方、満期・６か月後に原資産Ａの株価が高騰して、時価２００万円になった場合は、このオプションを「行使」することで、差額分だけ利得が発生します。

 このように、オプションを適正に行使する（または放棄する）事で、原資産（金融資産など）の価格変動のリスクをヘッジすることができるのです。

 ある価値を有する原資産Ｓ(ｔ)を，満期Ｔの時点で権利行使価格Ｋ円（ストライク）で購入できるオプションを考えます。この時、Ｓ(Ｔ)がインデックスに相当します。

 満期Tの時点で原資産の価値が暴落し、時価がＫを下回れば、オプションを放棄することで損失を回避できます。

 一方、原資産の価値が高騰し、時価がＫを上回れば、権利を行使することで利得ｈ(Ｓ)＝Ｓ(Ｔ)－Ｋが発生するのです。この取引の結果生じる利得ｈ(Ｓ)のことをペイオフ関数と言います。


 オプション取引を行う際は、予めその権利を購入する必要があります。この権利のお値段、つまりオプションの価格（価値）のことを「プレミアム」と言います。

 オプション取引に伴う利得は青のグラフ（ペイオフ関数）で表されますが、実際には既にプレミアムを支払っている状態なので、実際の収支は青のグラフよりもプレミアム分だけ下にシフトした赤のグラフのようになります。

 プレミアムは、将来時点Ｔで見込める利得を、現在時点（契約時点）での価値に換算したものです。

 オプション取引では、原資産の価値が時間と共に変動しています。これに伴って、オプションの価値・プレミアムもまた、時間的に変動しています。その変動は原資産（危険資産）と同様に、確率微分方程式で表現されます。


 ここまで、安全資産・危険資産、そしてプレミアムの微分方程式やリスクの市場価格の式を導いてきました。これらの式を基にして、プレミアムに関する方程式を導くことが出来ます。

 このBlack-Scholesの偏微分方程式に変数変換を施して熱伝導方程式に変換し、オプション取引の条件を適用した上で、解の重ね合わせ（積分）を行うことで、次のようなプレミアムの公式を得ることが出来ます。

 これがBlack-Scholesの公式です。


 また、原資産Ｓ(ｔ)が指数関数で表され、その指数が正規分布に従うと仮定されることから、Ｓ(ｔ)は対数正規分布に従うと仮定されます。正規分布と対数正規分布の関係について、補足しておきます。

金融資産の組合せ・ポートフォリオ

 資産運用の際は、様々な金融資産を組み合わせて保有することが多いわけですが、この金融資産の組合せ（構成）を「ポートフォリオ」を言います。ここでは簡単のため、２種類の金融資産ＡとＢの場合を考えてみます。

 金融資産Ａはリターンがμ_A，リスクはσ_Aであり、金融資産Ｂはリターンがμ_B，リスクはσ_Bであるとします。この両者のバランスに応じて、ポートフォリオは変わります。いま、リスクσを横軸、リターンμを縦軸にとってグラフを描いています。

 金融資産Ａが100%のポートフォリオは（σ_A,μ_A）、金融資産Ｂが100%のポートフォリオは（σ_B,μ_B）となります。そして、この２点を端点とする曲線（線分）ＡＢが、２種類の金融資産ＡとＢを任意の割合で組み合わせたポートフォリオの集合です。

 ここで、左側に凸となる頂点に相当するポートフォリオは、最もリスク（標準偏差＝分散の平方根）が少ないことから、「最小分散ポートフォリオ」と呼ばれています。

 また、最小分散ポートフォリオよりも上側の部分を有効フロンティアと言います。同じリスクに対して、より大きなリターンを見込める（＝有効である）ということです。


 それでは、２種類の金融資産ＡとＢの最適なポートフォリオはどのようにして決まるのか、について考えてみます。新たに、リターンがｒ，リスクは０の無リスク資産を仮定します。リスクを取らなくても、既にｒのリターンが得られるという条件です。

 この無リスク資産（０,ｒ）から、有効フロンティアに向かって接線を引きます。この時の接点に相当するポートフォリオ（σ_M,μ_M）が最適な組合わせとされています。

 また、接線の傾きをリスクの市場価格λと言います。もともと、リスクを冒さずしてｒのリターンが得られるのに、敢えてσだけのリスクを冒すことで、μ－ｒだけリターンを上乗せすることが出来る、という意味です。冒すリスクに対して、どれだけの追加リターンが期待できるか、の指標です。

安全資産と危険資産の考え方

 現在時点における価値（元金）がS₀の試算を年利ｒで運用する場合、この資産のｔ年後の価値は、現在の価値に「e^rt」を乗じることで、S₀e^rtとなります。このような将来時点における価格のことを「フォワード価格」という事があります。

 また、将来時点（ｔ年後）の価値が判っている時に、これを現在の価値に換算する場合は、将来の価値に「e^-rt」を乗じることで計算することが出来ます。この乗数を「ディスカウント・ファクター」と言います。

 また、資産価値の関数Ｓ(ｔ)を微分すると、次のような微分方程式が得られます。

 ある時点（期間）での元金をＳとして、利率ｒの連続金利を適用した場合、期間Δｔの間に利子ΔＳが発生したとすると、「（利子）／（元金）＝（利率）×（期間）」の関係が成り立ちます。


 さて、定期預金のように、普通の複利法であれば、例えば１年毎のように「定期的に」利子が上乗せされます。これに対して、連続複利を用いると、利子は連続的に上乗せされるため、資産価値の時間変動は連続的なものとなります。

 このように、安定的に資産価値が上昇する金融資産を安全資産と言います。安全資産は記号Ｂ(ｔ)で表します。

 左が資産価値の時間変化のグラフで、右が利子の確率分布です。安全資産では利子は常に一定として扱うため、利子ｒの出現確率が１となります。

 一方、株価などのように、その資産価値が時々刻々と上下に激しく変動する金融資産（金融商品）もあります。

 このような資産を運用した場合、大きな利益を上げることも期待できる半面、元本割れを起こしてしまう危険性もはらんでいます。このような金融資産を危険資産と言います。

 危険資産を数理モデルで表現する際は、平均的な変動（トレンド）は安全資産に準じるものとして、さらに不規則に変動する成分（ノイズ）を考慮します。

 トレンドは安全資産に準ずるものとして、その利率をμと表すことにします。このμは平均的な利率（利益率）に相当し、「リターン」と言います。

 また、このノイズはブラウン運動に従うものとし、これをｚ(ｔ)とします。また、この振動の振幅をσとします。このσは利率（利益率）の変動の幅の大きさに相当し、「ボラティリティ」または「リスク」と言います。

連続複利の概念

 複利法とは、元金によって生じた利子を次期（次年）の元金に組み込んでいく方式です。例えば「元金をS₀,年利をr」の条件で預金すると、次のように預金額は増えて行きます。

 １年後には元金S₀に利子S₀r（＝利率×元金）が新たに組み込まれる形で、元利合計（預金額）が増えていきます。

 ２年後には元金S₁に利子S₁r（＝利率×元金）が新たに組み込まれる形で、元利合計（預金額）が増えていきます。

 つまり、１年後の預金額をS₁、２年後の預金額をS₂…ｔ年後の預金額をS_tとすると、この間預金の出し入れや、利率の見直しが発生しないものと仮定すると

（ｔ年後の預金額）＝（元金）×｛１＋（利率）｝^（年数）

のように表すことができます。

 上の例では１年ごとに利子が上乗せされる条件（１年複利）を想定しました。これがもし、半年ごとに利子を上乗せする場合（半年複利）は、１年を２期に分けるので、半年ごとに利率(ｒ/２)分ずつ、つまり、１年の間に２回、利子が上乗せされます。

 同様にして、１年をｎ期に分ける場合（１/ｎ年複利）は、１/ｎ年ごとに利率(ｒ/ｎ)分ずつ、つまり、１年の間にｎ回、利子が上乗せされます。この回数ｎを∞に持っていくと、連続的に利子が上乗せされることになります。つまり、連続的に預金が増加するということです。

 ネイピア数eを用いると、１年後の元利合計S₁は簡単に記述することができます。

 ここで、元金をS₀,年利をrの連続複利で運用する場合を考えてみます。この場合、次のようになるので

 このイメージをグラフで表してみます。

 通常の１年複利や半年複利の場合は、１年毎または半年毎に元利合計が増えて行くので、資産価値は階段状に上っていきます。この感覚を細かくしていくと、やがて、滑らかなカーブに近づいていきます。このカーブが連続複利に相当します。実際問題としては一定の時間間隔ごとに、段階的に預金が増加する（利子が上乗せされる）わけですが、理論的に解析する際は、連続的な関数の方が数学的にも扱いやすいので、連続金利を用います。