前回の記事では「連続体の運動方程式」を導出しました。そこで今回はさらに「粘性流体の構成方程式」と「非圧縮性流体の連続の式」を適用することで、流体力学の方程式を導きます。
まずは「ナビエ・ストークス方程式」を導出し、その後は簡単な条件を設定することで「ベルヌーイの定理」を導出します。今回使用するのは次の4つの式です。

まずは、「加速度の定義式」と「粘性流体の構成方程式(応力と速度の関係式)」を「運動方程式」に代入します。その後、一部の項が「連続の式」の形となって消去されます。この結果、「ナビエ・ストークス方程式」の形が現れます。
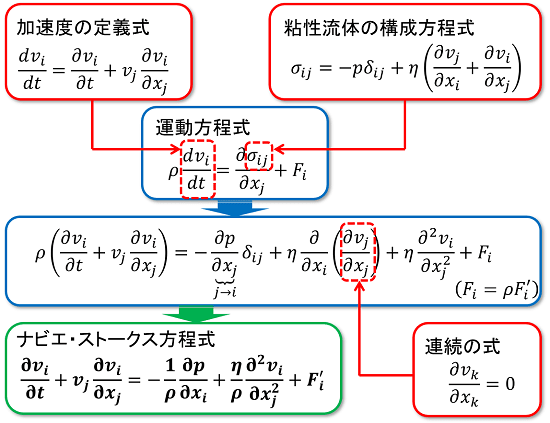
続いて、ベルヌーイの定理を導いてみましょう。
次図のx‐z系において、青い流線で表される流れを想定します。ここでx軸は水平方向、z軸は鉛直方向に対応し、重力はz軸の負の方向に働くと仮定します。ここでは理想流体を考えるため、粘性係数ηはゼロとします。また簡単のため、流線に沿った1次元の定常流れとしましょう。
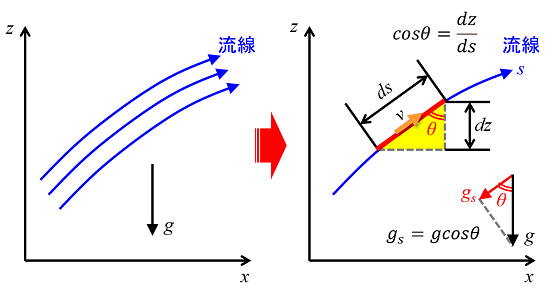
このような条件下で、流線sに沿ってナビエ・ストークス方程式を立てると次のように表されます。後は、これを流線sに沿って積分すれば良いのです。この結果、ベルヌーイの定理の式が得られます。
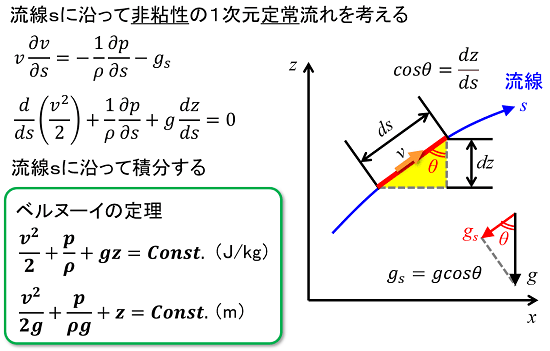
ここでは、ベルヌーイの定理の式を2種類書いています。上の式は各項が「単位質量辺りのエネルギー」で表されるのに対し、下の式は各項は「水頭(ヘッド)」で表されています。但し、数式自体は同じものなので、必要に応じて使い分けると良いでしょう。
ベルヌーイの定理の応用例として2つ紹介します。まずは「ポンプ」です。ポンプは、その機械的作用によって、作動流体にエネルギーを付加するものです。
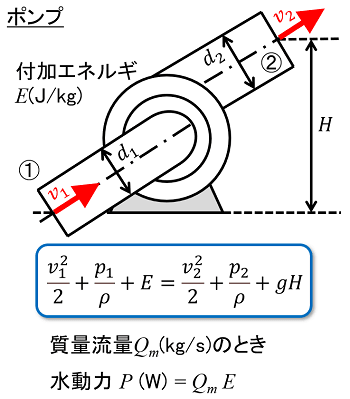
下の流入口(状態1)から流体を吸い上げて、上の流出口(状態2)から吐出する場合を考えてみます。作動流体の持つエネルギーは、状態1より状態2の方が高くなります。
この時、ベルヌーイの定理の式(エネルギーで表示)は、次の関係を表しています。
(状態1のエネルギー)+(ポンプによって付加されたエネルギー)=(状態2のエネルギー)
続いて、管を通る流れです。水槽から接続された円管を通って、作動流体が流れ出る場合を考えてみましょう。
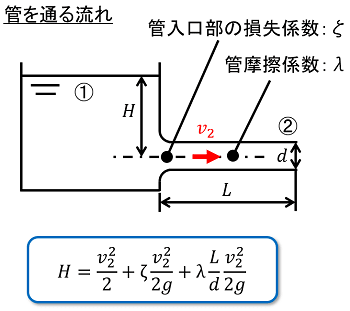
(状態1)では作動流体は静止していますが、位置エネルギーを持っています。一方、管の出口の(状態2)では、作動流体が速度v2で流出しています。
作動流体の持つエネルギーは、状態1より状態2の方が低くなります。これは、管の入口(接続部)や管路の摩擦に伴うエネルギーの損失が生じるためです。
この時、ベルヌーイの定理の式(ヘッドで表示)は、次の関係を表しています。
(状態1のエネルギー)=(状態2のエネルギー)+(管入口の損失)+(管摩擦損失)
まずは「ナビエ・ストークス方程式」を導出し、その後は簡単な条件を設定することで「ベルヌーイの定理」を導出します。今回使用するのは次の4つの式です。

まずは、「加速度の定義式」と「粘性流体の構成方程式(応力と速度の関係式)」を「運動方程式」に代入します。その後、一部の項が「連続の式」の形となって消去されます。この結果、「ナビエ・ストークス方程式」の形が現れます。

続いて、ベルヌーイの定理を導いてみましょう。
次図のx‐z系において、青い流線で表される流れを想定します。ここでx軸は水平方向、z軸は鉛直方向に対応し、重力はz軸の負の方向に働くと仮定します。ここでは理想流体を考えるため、粘性係数ηはゼロとします。また簡単のため、流線に沿った1次元の定常流れとしましょう。

このような条件下で、流線sに沿ってナビエ・ストークス方程式を立てると次のように表されます。後は、これを流線sに沿って積分すれば良いのです。この結果、ベルヌーイの定理の式が得られます。

ここでは、ベルヌーイの定理の式を2種類書いています。上の式は各項が「単位質量辺りのエネルギー」で表されるのに対し、下の式は各項は「水頭(ヘッド)」で表されています。但し、数式自体は同じものなので、必要に応じて使い分けると良いでしょう。
ベルヌーイの定理の応用例として2つ紹介します。まずは「ポンプ」です。ポンプは、その機械的作用によって、作動流体にエネルギーを付加するものです。

下の流入口(状態1)から流体を吸い上げて、上の流出口(状態2)から吐出する場合を考えてみます。作動流体の持つエネルギーは、状態1より状態2の方が高くなります。
この時、ベルヌーイの定理の式(エネルギーで表示)は、次の関係を表しています。
(状態1のエネルギー)+(ポンプによって付加されたエネルギー)=(状態2のエネルギー)
続いて、管を通る流れです。水槽から接続された円管を通って、作動流体が流れ出る場合を考えてみましょう。

(状態1)では作動流体は静止していますが、位置エネルギーを持っています。一方、管の出口の(状態2)では、作動流体が速度v2で流出しています。
作動流体の持つエネルギーは、状態1より状態2の方が低くなります。これは、管の入口(接続部)や管路の摩擦に伴うエネルギーの損失が生じるためです。
この時、ベルヌーイの定理の式(ヘッドで表示)は、次の関係を表しています。
(状態1のエネルギー)=(状態2のエネルギー)+(管入口の損失)+(管摩擦損失)

















