たまには「計算気象」の取り組みについて書いてみる。

【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897844094.html


　最近、ブログでも全然触れていませんが、一応「工学的手法で局地気象にアプローチする」のが本来の専門分野です。

　というわけで・・・学術研究の一環として、独自に開発を進めている３次元熱流体数値モデルによるシミュレーションの一例の紹介です。今回は西北西寄りの強い流れ場を想定した計算結果です。基礎方程式は、熱流体方程式（ナビエ・ストークス方程式＋熱エネルギー方程式）に乱流モデルを搭載したものです。

　今回は、流れの様子を流線で表示してみました。ベクトルで表示する場合とは違って、流れの全体的な様子が判りやすくなりました。中部山岳による影響も現れているようですね。しかし、もともとの接近流の流れが速いこともあってか、慣性が勝っているようにも見えます。

マニュアル解析と線形内挿に基づいた解析の比較

【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843947.html


　先日、2012年11月17日のブログ御紹介した、山形県内の冬の間（１～２月の２か月間）の平均的な積算降雪量の分布を、マニュアルの等値線解析とコンピュータによる線形内挿に基づいた解析の両方で可視化し、その結果を比較してみました。


(※画像をクリックすると拡大します。)

　どちらも冬の間（１～２月の２か月間）における２ヶ月積算降雪量 (2001～2012年の平均値：単位は[cm])で、左がマニュアル解析、右が線形内挿に基づいた解析です。基となる気象観測データは、アメダスの降積雪量を使用しています。

　概ね同じような特徴が解析されており、降水量と降雪量の特に多い領域（極大域）は、朝日連峰の位置と概ね重なっており、その右側（東側）では降水量と降雪量の特に少ない領域（極小域）が目立っています。

　以前、2007年03月15日のブログでは、点在する観測データからメッシュ推定値を計算する取り組みを紹介しておりましたが、それから幾多の試行錯誤を経て、漸く簡単な手法で点在する数値データを面的に展開する手法を独自に考案するに至りました。

円筒座標系の熱流体方程式と熱ロスビー波

【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843899.html


　大気大循環に伴う波動発生のメカニズムは、例えば北極と見做した中心を氷等で冷やした回転二重円筒間の流れ(熱ロスビー波)で模擬される事が知られています。そこで今回はこの実験に倣って、半径方向に温度勾配を与えられながら、一定の回転角速度で回転し続ける二重円筒形状容器を考え、その内部に充填された試験流体の熱流動の数値シミュレーションを独自に開発して波動の再現を試みました。

　解析に用いる基礎方程式は、次のような連立非線形偏微分方程式です。

【円筒座標系で表現される強制対流のNavier-Stokes方程式】
　（∂ｖ/∂ｔ）＋（ｖ・∇）ｖ＋２ω×ｖ＝－∇ｐ＋（１/Ｒｅ）∇²ｖ＋（Ｇｒ/Ｒｅ²）Ｔδ_i3

【円筒座標系で表現される熱エネルギー方程式】
　（∂Ｔ/∂ｔ）＋（ｖ・∇）Ｔ＋２ω×ｖ＝（１/Ｐｒ・Ｒｅ）∇²Ｔ

【微分演算子とベクトル】
　∇＝（∂/∂ｒ）＋（∂/ｒ∂θ）＋（∂/∂ｚ），ｖ＝（ｖ_ｒ，ｖ_θ，ｖ_ｚ）

　ここで、ｖ_ｒ、ｖ_θ、ｖ_ｚは各々半径方向、円周方向、鉛直方向の速度成分であり、ｐ、Ｔは各々圧力、温度である。また、Ｒｅ、Ｇｒ、Ｐｒは各々Reynolds数、Grashof数、Prandtl数である。

　今回想定する実験装置(数値モデル)の概要は次のようなイメージです。

　

　実験装置は半径r_０及びr_１の二重円筒で構成されており、内側の円筒を冷源T_ｃとし、外側の容器内に試験流体が充填されるものとします。更に外側の容器の周囲には一様な熱源T_ｈが分布しているものとします。

　そして、この実験装置全体を一定角速度ω_０で反時計回りに回転させます。

　ここで、寸法はΔr= r_１－r_０を基準として、r_０＝Δr、r_１＝2Δr,z＝Δr/2に設定しました。 従って、Reynolds数は試験流体の動粘度係数νを用いてRe=ω_０(Δr)^２ /νで表され、Grashof数は体膨張率β_０、重力加速度gを用いる事により、Gr＝gβ_０(T_ｈ－T_ｃ)×(Δr)^３ /ν^２で表されます。

　続いて、初期条件・境界条件の概要は次のような形です。

　壁面摩擦を受けない場合v_θは単純にv_θ＝ｒωに従うため、最外周で極大となります。しかし、実際には壁面摩擦を受けるので内壁面および最外周壁面上ではθ方向の速度は0にならなければいけません。初期状態においてはこの境界条件を満足する発達した流れを想定し、v_θ(r)はr方向に放物状の速度分布を成すものと仮定します。

　また、温度に関する境界条件は、内側円筒に相当するr≦r_０は冷源であるため T=T_ｃ、最外周壁面に相当するr=r_１は熱源であるため T=T_ｈです。初期条件は、r_０≦r≦r_０+Δr/2では試験流体が冷却されているため T=T_０とし、r_０+Δr/2≦r≦r_１では試験流体が加熱されているためT=T_０＋ΔTとします。

　今回はGr＝1.0×10^２,Re＝3.0×10^２,Pr＝0.71の条件を設定し,３次元熱流動の数値シミュレーションを行いました。その結果は・・・。

　こちらは、円筒の高さの半分に相当するZ=Δr/4における水平面上の温度と流れの様子を解析した結果です。波数5の熱ロスビー波が形成されているのが分かります。波が中心に向かって盛り上がる位相(リッジ)の右側では時計回り、左側では反時計周りの渦が形成されています。一方、中心から遠ざかる位相(トラフ)ではこれとは反対の構造になっています。

　続いてこちらは、この水平面上における鉛直渦度ζと流れの様子を解析した結果です。

　正渦度域(ζ>0)と負渦度域(ζ<0)が交互に形成されている事が分かります。従って、トラフの右側(リッジの左側)では正渦度循環、リッジの右側(トラフの左側)では負渦度循環が形成される現象が再現されました。

山越え気流の解析モデル

【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843642.html


　いよいよ５月に入りました。学会発表も間近に迫ってきています。今回は「新潟県内における冬の季節風と陸風によるシアーライン発生の数値実験」と題して、また新しい数値シミュレーションを試みました。数値実験を色々と試行する事で、想定した条件に対する局地気象のレスポンスを探ってみました・・・。そんなわけで、もう一度、基本的な知識をおさらいしてみようと思います。


　さて、日本の国土の多くは急峻な山岳地形ですので、局地気象の基本として山岳地形の影響を考える必要があります。この出発点となるのが山岳地形を乗り越える気流の解析(山越え気流)です。山越え気流の問題は局地気象の古典的な問題として多くの研究者によって解析が行われてきました。

　まずは、山越え気流の中でも良く知られているフェーン現象を例に挙げてみましょう。一般にフェーン現象は、山を乗り越えて吹き降りる風が高温になる現象ですが、大きく分けると次の二種類があります。一つ目は様々な気象の記事や教科書等で目にする湿ったフェーン(熱力学的フェーン／ウェットフェーン)であり、もう一つは相変化を伴わない乾いたフェーン(力学的フェーン／ドライフェーン)です。

図1.二種類のフェーン現象

　飽和した空気の高度に伴う気温変化率(dT/dz)は約0.5℃/100mですが、乾燥した空気の気温変化率(dT/dz)は約1.0℃/100m(乾燥断熱減率)となります。湿ったフェーンは、山を乗り越える際はdT/dz≒0.5℃/100m(湿潤断熱減率)の割合で降温する傍ら、山頂付近で水分が凝結→降水を経て空気の外に出て行くために空気自身は乾燥し、山の斜面を吹き降りる際にはdT/dz≒1.0℃/100mで昇温していきます。

　一方、乾いたフェーンは、山頂付近を流れる風が、山頂を越えた後に力学的な要因により急降下する事に伴い、断熱圧縮されるために昇温するものです。実際には乾いたフェーンと湿ったフェーンの発生ウェイトは、最新の研究報告によると「乾いたフェーンが80.8%、湿ったフェーンが19.2%」と言われています(※2021年11月24日・追記)。乾いたフェーンのように、山頂付近の流れが急降下して風下側の麓に強風として吹き降りる現象をおろしとも言います。

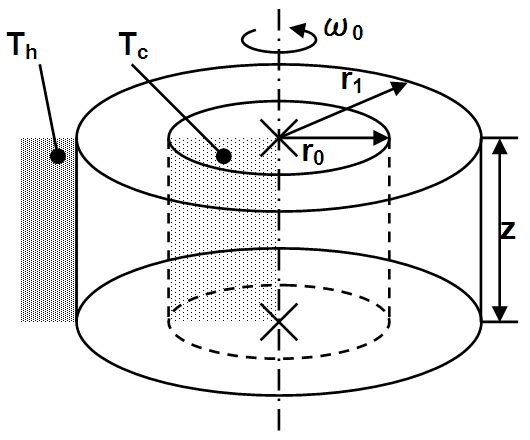
図2.山越え気流のモデル化 (定常流れの理論に基づく)

　図2にはこのメカニズムの解析モデルを示しました。ある高さH₀[m]における等圧面を点線で表し、これを自由表面と呼びましょう。地表面付近の大気(上空数km程度←山岳標高の２倍程度を目安)を、自由表面を境に上下２つの層に分ける二層構造で考えます。そして、下側の層の温位(ポテンシャル温度)をθ₀[K]、上側の層の温位を少し高めのθ₀＋Δθ[K]であるとしましょう。この温位(ポテンシャル温度)とは温度に替わるパラメータです。また、左側から速度u₀[m/s]の風が流入するものと考えましょう。そうすると、次に示すフルード数Frの大小によって山を乗り越える流れの様子が大きく変化します。フルード数の定義には、流入速度u₀の大小が反映されているため、u₀が大きいほど(Frが大きいほど)流れは山を乗り越えやすく、風下でのおろしが発生しやすいのです。

Fr = u₀ / { g (Δθ / θ₀ ) H₀ } ^0.5

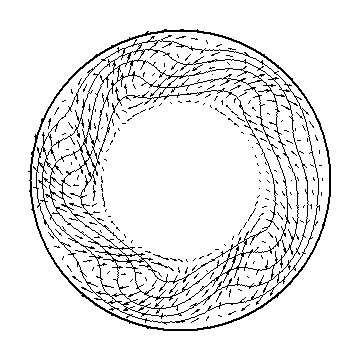
図3.山越え気流の数値シミュレーション

　図3には、山越え気流の数値シミュレーションの解析例を掲載しました。初期状態として、図2のような大気の二層構造を考え、自由表面は水平であるものと仮定しました。境界条件としては、左端面から右方へ向かう一様な水平流u₀が安定して流入し、右端面から流出していくものとします。そして、この流路の途中に山岳地形を模して三角形の山を置くものとします。この時、流れが山を乗り越える際の流れの特性の違いを見てみましょう。

　上の低フルード数では自由表面は山頂付近で凹状に僅かに陥没しましたが、ほぼ初期状態(＝水平状態)を維持しています。山頂付近で風速が一時的に強化された後も、そのまま水平な流れを維持しながら減速傾向にあるといえます。一方、下の高フルード数の場合では、自由表面は波状にうねり、風下側の麓に向かって風が強く吹き降りる様子が解析されおり、図2の特性が再現されているのが判ります。

　このような山越え気流のシミュレーションは、多くの研究者によって既に解析されております。それは換言すると、シンプルでありながら実に奥が深い、という事の現れでもあるように感じます。この解析モデルの考え方を応用して、実際の詳細な地形条件を考慮した三次元の熱流体解析を行った事例を次の紹介しましょう。

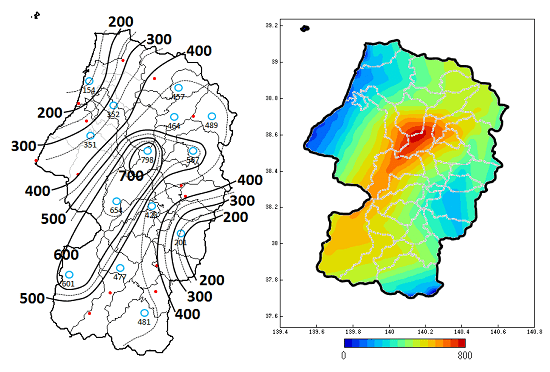
図4.冬型の気圧配置となる条件下での山形県置賜地方におけるフルード数と局地風の関係

　まずは冬型の気圧配置となる条件下での山形県置賜地方におけるフルード数と局地風の関係を解析です。局地風は、フルード数が低い場合は季節風とは異なり南よりの風向が卓越する一方、フルード数が高い場合は季節風に沿って西よりの風向が卓越する特性が解析されました。

図5.新潟県上越地方のドライフェーンに伴う高温域

　続いて、新潟県上越地方のドライフェーンに伴う高温域の再現実験です。局地風系と気温の特徴(高温域の発生)は、数値モデルの単純さにも関わらず良く再現されましたが、高温域の気温が実際のケースよりも若干高めに計算される等の誤差も見受けられました。

　このように、二層構造による山越え気流の解析モデルはシンプルな構造でありながら、幅広く応用が効くのです。但し、フルード数やそれに関わる各種のパラメータの決め方で、毎回悩むんですよね・・・。

(p.s.)
さらに詳しいシミュレーションを「山越え気流の２次元解析」に掲載しています。

不規則に点在するデータからパラメータの空間分布を推定する・・・

【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843622.html


　約一週間後に公立高校入試を控えている事もあり、ほぼ毎日のペースで学習塾の教室に(受験指導に)通う傍ら、肝心の計算局地気象の専門家としては、「不規則に点在する数値データ群から規則的に配置されたメッシュ上におけるパラメータの値を推定し、その分布を滑らかに補正する数値解析技術」を研究しています。これまでにもこの手の研究開発には何度も挑戦してきましたが、今回はまた新しい計算手法を用いました。漸く、一つのプロトタイプが出来上がりました（逆に言えば、それまでの試みは殆どが失敗だったという事）。これまで試行錯誤を繰り返しながら積み重ねてきた、多くの知恵と経験を組み合わせて、それがやがて一つのプログラムの形になり、その計算結果がこのような形で見えるようになると感激ですね。

　このような解析を進めていくに当たっては、ただ単に天気予報や気象学の知識のみならず、物理学や数学、さらにプログラミングに関する幅広い知識と、実際にこれらの知識を駆使しての気象データ解析の試行錯誤の経験が必要になります。むしろ、天気や気象よりも数的処理（数学やプログラミング）の知識のウェイトの方が高いかも知れません。色々な専門分野の世界に身を置いて、勉強してきた知識と経験が、長い時間を経て、様々な形で活き始めています。

建造物内の熱流動シミュレーション

【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843575.html


　屋外で風が吹いている日に建物の窓を開けた場合、外の風が屋内に入ると室内の熱環境がどのように変化するのかを解析してみました。解析結果のほんの一例です。

建造物の平面図と熱流動（左：１階、右：２階）

建造物の鉛直断面図（階段・吹き抜け部）

　初期状態では室内には熱が篭もっている状況を想定しました。初期状態における室内の温度を赤、外の温度を青で表示し、図の右側から風が流れ込む条件を与えました。時間の経過と共に外からの涼しい空気が室内に入り込んで、建物内部での空気のかき混ぜが起こって行く様子が再現されています。

建造物の通風・換気シミュレーション

【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843573.html


　屋外で風が吹いている日に建物の窓を開けた場合、外の風が屋内に入るとどのような気流を形成するのかを解析してみました。解析結果のほんの一例です。


　図１・建物の１階における風の流れの様子(水平断面図)
　真ん中の長方形が階段に相当。左上の長方形はシステムキッチンに相当。


　図２・建物の１階における風の流れの様子(水平断面図)


　図３・階段の吹き抜け部の風の流れの様子(鉛直断面図)

　このような気流の解析の際は、建造物の数値モデルを用意する必要があります。もちろん、局地気象モデルであれば山岳地形の数値モデルが必要になるのです。山岳地形の場合は既に様々なＤＥＭ（数値地形モデル）が整備されておりますが、建造物の場合はその都度、自分でモデルを構築しなければなりません。しかも、単なる凹凸の組合せではなく、ボックスの配置を一つ一つ３次元的に設定しなければなりません。

　このため、まずは建造物の構造をプログラム言語のようなコード形式で記述する方法を考案し、このコード記述から数値モデルに自動変換するプログラムを作成しました。気流解析（熱流体解析）のプログラムは既にある３次元ＬＥＳの局地気象モデルをベースに応用しました。

　ぶっちゃけ、建造物の構造をコードで記述するのが面倒です(爆)。もちろん、建築設計事務所など、建設系のシミュレーションを行う企業向けには専用のＣＡＤ／ＣＡＥツールも用意されているようですが・・・導入価格がン百万円のオーダーです。建築用図面の電子データをそのまま読み込んでシミュレーションまで自動的に行うようなツールですので、その位の高価なソフトウェアになるのも無理もないのでしょう・・・。

　こうやって、計算解析の技術も日夜研究を続けているのです・・・。

スカラー移流過程の試解析

【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843545.html


　事業計画書案(アイデア提案)も期限内に無事に提出した所で、数値シミュレーションの試計算結果を整理しています。三次元の数値計算プログラムは問題なく動作するようになりました。次の課題は「如何にして適切な計算条件を設定するか」です。

　局地的な気象特性のメカニズムを考察する際は気象観測データや局地天気図から考察する事が多いのですが、実際に数値シミュレーションを行って見ると新たな発見に出くわす事もあります。このような時はやっぱり目からウロコという心境になります。

海陸風の数値シミュレーション

【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843514.html


　さて、久々に数値シミュレーション解析の話題を一つ。


　
　こちらは海陸風を簡単な構造で表現して計算した結果です。海陸風のシミュレーションはＣＦＤの参考書籍でも良く取り上げられます。今回の計算では、計算領域の左半分を海上、右半分を陸上としています。初期状態では、左半分では既に海面からある程度の高さまで空気が十分に冷やされる一方、右半分では地面からある程度の高さまで空気が既に十分に熱せられており、ある程度の高さより上の層では温度は寒暖の中間の状態であると仮定しています。また、境界条件では海面上は冷源、陸面上は熱源であるとしています。

　地面及び海面付近では、海からの冷気が陸上に流れ込み、上空では陸上の暖気が海上に流れ込んでいる事がわかります。これに伴って海陸間で鉛直循環が生成されるわけです。このような海陸風の影響が局地気象の解析で重要となるのは、例えばこんな数値シミュレーションを行う場合です。



　これは私が今年の春の気象学会で発表した新潟県上越地方のフェーンに伴う高温域の解析事例です。沿岸部における気温の誤差が内陸地に比べて大きく、沿岸部ゆえの海陸間の熱容量の違いに伴う熱的条件の考慮・反映が今後の課題となっています。そこで、このような局地気象の地域特有の特性を形作る基本的な現象のメカニズムのモデリングの検討を進めています。

　熱流体数値モデルによる解析を進める際に、どのような初期条件や境界条件を与えるか・・・すなわちどのようなメカニズムや気象場を与えるかが重要になってきます。

工業設計と数値シミュレーション・・・ＣＡＥ解析

【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843459.html


　ＣＡＥとは「Computer Aided Engineering」の略で、主に「コンピュータによる設計支援」等と訳されます。コンピュータによる高度な科学技術計算を用いて、様々な工業製品の変形・熱流動等の挙動に関する予測（数値シミュレーション）を行なう事で設計開発に役立てようとするものです。

　従来の製品開発では、工学便覧に載っているような簡易計算で行っており、実物（試作品）が出来るまでその設計の良し悪しがわかりませんでした。そのため、実際に試作品を製作して、耐久試験や性能評価を何度も行って製造方法の妥当性を検証したりしていました。このような方法では、コストもリードタイムも多く必要とし、また試作できる回数も限られることから最適な設計の追求も十分ではない等の課題がありました。

　この手法に替わるものとして、コンピュータ上に工業製品を模擬した物理モデルを構築し数値シミュレーションを行う事で設計内容の検証を行う手法が確立されました。これにより現実には観察が難しい現象のシミュレーションも行なえるようになりました。現在では構造解析や熱流体解析、電磁気解析をはじめ多種多様なＣＡＥソフト(ツール)が市販されているようですし、受託解析を行う企業もあるようです。

　但し、ＣＡＥが発達したからと言って実物での評価が全く不要と言う事になりません。モデルに反映されていない条件や見落としている何かが無いとは言い切れないからです。モデルはあくまでモデルに過ぎず、実物に取って代わるものではありません。ただ、設計段階においての当該設計の是否を判断する上では大きな判断材料となる事は確かです。この事は数値予報モデルも一種のＣＡＥツールである、と考えれば理解しやすいのではないでしょうか。

　私も以前、半導体の設計部門に所属していたので、論理回路設計に関わった事があります。その設計でもＥＷＳ上での専門ツールを用いた論理合成や半導体回路の動作シミュレーションを繰り返しました。

　半導体の論理回路はＡＮＤ回路やＯＲ回路、ＮＯＴ回路の組み合わせ・・・いや、実際のＣＭＯＳ集積回路はＮＯＴ、ＮＡＮＤ、ＮＯＲ等の負論理の組み合わせで表現されます。しかし、その設計段階ではプログラミング言語のようなコーディングを行い、そのコードをツールを使って負論理（論理ゲート）の組み合わせに変換して行きます（論理合成）。

　そして、半導体素子を動かすプログラムをアセンブラ言語で記述して、合成された論理回路が期待通りの動作をするかを、シミュレートします（論理シミュレーション）。さらには、特定の論理ゲート（もしくはセル）に遅延を与えて（物理的な特性をモデル化）、信号の伝播への影響を調べる事もあります。

　このような過程を繰り返して論理回路を決定すると、今度はその論理回路を実際のＣＭＯＳトランジスタの組み合わせで表現します（デバイス設計）。この段階で半導体素子の仕様寸法内の収まるようにＣＭＯＳの配置（レイアウト）も設計するためレイアウト設計とも呼ばれます。ここでも専用のツールが登場します。

　さらに試作品（サンプル）も製造して電気的、機能的性能の評価も行います。その際には一つ一つのサンプルが正常に動作するか否かをチェックする必要があります。ここでは巨大な機械・テスター（１台数千万～１億円程度！）を用います。一つ一つにサンプルをテスターに設置して、テスターを操作してサンプルに様々な電気信号を与えます。その入力に応じてのリアクションが期待通りのものかどうかを逐次判定し、当該サンプルが正常が否かを判定するのです。

　設計段階では物理的・論理的なモデルを多用したツールが多用されますが、それでも見落としや不具合が発生する事があります。ヒューマンエラーもありますが、ツールのモデリングが不十分と言う事もあります。当時は「ツールを過信するな」とは良く言われたものです。

　新卒での就職活動の折、気象業界を志望して夢破れましたが、それからは目からウロコが落ちたかのようにバイオ系企業やメーカーにも応募するようになりました。その時、ＣＡＥ解析にも関心はありましたが、そのような専門企業は既に採用が終わっていた（または敷居が高すぎて応募に至らなかった）と言う経験があります。

　それ以来「ＣＡＥ解析」という言葉に触れる事はありませんでした。しかし考えてみると、今やっている事がＣＡＥ解析につながっていると言う事に気付きました。今は直接に工業設計に携わっているわけではありませんが、もう少し、工業的な応用にも目を向けて行きたいと感じました。

偏微分方程式を通じて局地気象を理解する・・・

【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843433.html


　Ｃ言語も漸く入門者レベルに達した所で、再び理論研究に戻っている最近です。

　これまでずっと引きずっている境界条件の問題は、「異なる方向の流れが多重構造を形成する場合の乱流解析」へと発展し、もはや境界条件だけの問題にクローズすること自体がナンセンスではないか、との心境に達しています。むしろ根本的に、そもそもどのように解析を進めるか、そしてそれは数学的に問題は無いのか？これは究極的にはNavier-Stokes方程式の厳密解が得られなければ分からないのかもしれません。しかし、それを待っていたのでは目の前にある問題はいつまで経っても解決しないでしょう。限界があるかもしれませんが、その中で最大限の活路を見出すしかない、という訳である意味、新たな悟りを開いたような感じです。

　その際のヒントが得られるかどうかは分からないのですが、今頃になって？偏微分方程式を解くと言うことについて勉強し直しています。偏微分方程式の解き方(計算方法)という事ではなく、それよりも偏微分方程式を解析的に解くと言う事について理解したいと思っています（そもそも計算方法については、ぶっちゃけ離散化して差分スキームを組んでプログラミングすれば数値解は求まるので、それほど重要かつ緊急の課題ではありません）。

　これまでの研究を振り返ってみると、特定の偏微分方程式(Navier-Stokes方程式)を解く事に莫大なエネルギーを注いできたので、もう少し一般的な偏微分方程式についても勉強したいとかねがね思っていました。確かに、Navier-Stokes方程式を解く事で偏微分方程式に関する基本的な事項は勉強できています。従って、その途中で取りこぼしてきた部分をしっかり固めたいのです。もしかしたら、そこにヒントがあるかも知れないからです。

　本来、私の目指している研究は、局地気象を解き明かす事によって気象予測の面から社会に貢献する予定なのですが、皮肉な事に？その局地気象を解き明かす以前の問題で相当な苦戦を強いられている形になっています。

　無論、局地気象の研究も続けているのは言うまでもありません。今年の日本気象学会の春季大会は無理でも、秋季大会には何らかの研究成果をぶつけたいと思っております。なぜなら、秋季大会は仙台(＝つまり東北地方)で開催されるから・・・。さすがに現在抱えている境界条件の問題は出せませんが(爆)。

　偏微分方程式の数値解析というのは、これまたとんでもない分野に手を出してしまったものだ・・・そう思うときも正直、あります。しかし、現在の天気予報は詳細な観測データと莫大な数の連立非線形偏微分方程式の数値解析(＝数値予報)に支えられているのは揺ぎ無い事実です。これらの解析結果を基に、人間が未来の現象を判断するのです。

　気象予報士に対するイメージとしてお天気キャスターを連想する人は少なくないと思います(このブログの読者に限っては、少なくなってきたかと思いますが)。しかし、そのお天気キャスターやお天気お姉さんの予報、解説を、偏微分方程式の解析が支えているという事実(と書くと、極論にも感じられるが)はどこまで広く知られているのかは謎です。別に、知らなくても実際には全然、困りません。本当に独自の局地予報を行うための技術開発なり研究開発に従事する、ごく一部の技術者がしっかりしていれば、ほとんど問題ありません。

　私の場合は、難解な偏微分方程式を解く事を通じて、局地気象に関わり続けているのです。境界条件をどのように与えるか、個々の流れをどのように与えるか、一つ一つの現象をどのようにモデル化(単純化・抽象化して表現)するのか、これらの問題は気象学と密接に関わってきます。むしろ、他とは違う角度から局地気象を見ることが出来るのです。誰も知らない局地気象の一面を見続けているのかもしれません。

　一連の研究を開始した当初は、３次元乱流解析を実現すれば後は独自予報の実用化は十分可能だろう、と考えていましたが・・・甘かったですね。今、こうやって境界条件や初期条件など、偏微分方程式を取り巻く諸条件についての研究に重点をシフトしてみて初めて、見える、分かる事(もしくは感覚)が多々ありました。これらは天気図からは見る、知ることの出来ない新たな一面です。これが以前にお話した「独自の自然科学的世界観」の形成につながっていくのかも知れません。

　そもそも数値シミュレーション自体がここ30～40年の間に急速に発展している事もあり、まだまだ未知の領域が広がっているのでしょう。解析の根本となる理論は何百年もの歴史を経て洗練されてきました。シミュレーションについてはまだまだ手探りの部分も多いのではないかと思います。今、まさに暗中模索のドツボに嵌まっています。

　でも、そろそろＣ言語の初級レベルの勉強もしなくては・・・。いっその事、これからの数値解析は全部Ｃ言語で書いてしまうのも良いかも(爆)。

不思議な模様と思い出話

　さて、不思議な図を掲載してみました。これは一体なんでしょう・・・。

　実は私の皮膚の細胞を顕微鏡で拡大した写真です。

　と言うのは勿論「嘘」です(^o^)。動物細胞と植物細胞のどっちに見える？と言ったら、まあ植物細胞に近いでしょうね。この黒っぽいのが如何にも細胞壁に見えるじゃないですか！でもまあ、この細胞の形がいびつなのは動物細胞っぽいし・・・というわけで、

　これは私のマンションに飾っているチューリップの茎の細胞を拡大したものです。・・・エ？それも嘘だろ！？・・・ですか(信用ないですね～～^^;)。

　はい、嘘です(あっさり認めます)。

　それでは何故嘘だと分かるのでしょうか？まあ、

(1)冒頭で嘘をついているから、もう１回くらい嘘をつきそうな気がする(←鋭い！私の性格を読んでますね)
(2)マンションの部屋にお邪魔したことあるけどチューリップなんかなかったぞ！(←え？いつの話？)
(3)私のキャラクターからしてお花を愛するキャラじゃない！(←そうね、お花よりもお金かなぁ)
(4)なんとなく・・・嘘っぽかった。(←シックス・センスってヤツね)

・・・等々、色々な理由が考えられますが、ズバリ！オルガネラ(細胞内小器官)が映ってないじゃないですか！少なくとも細胞なら核を始めとするオルガネラが無いとおかしいのでは？と元バイオメカニクスの研究者はツッコむのであります。

　というわけで、一体この図は何なのだ？という所に戻りますが、実はこの２～３日この不思議な細胞？の研究をしておりました(とは言っても、実際に頑張っていたのはコンピュータなんですが・・・)。この一言で、ビビビと来た方は相当鋭いですね。これが綺麗な六角形になればベストなんですが、なかなかこれが難しい。

　要は、不安定成層場における熱対流セルの数値シミュレーションです。条件が合えばベナール型対流の綺麗な六角形状の構造を再現できる筈なのですが・・・その条件は未だ見つかっておりません。

　かつて前職の頃(３年以上前は半導体のエンジニアだった)は計算流体力学の専門書籍等を読んで、見よう見まねの渦度法(ζ-ψ法)で２次元の簡単なベナール型対流を再現していました。そういえばＧＰＶを細分化して、簡単な流れの数値解法にぶち込んで局地気象の予測に応用する、なんて研究もやっていましたね(しかも、これは本業ではなく、休日に行っていたのだ！！)。今思うと懐かしい思い出です。

　当時、職場の飲み会の度に必ず聞かれるのは、「休日は何してるの？」です。それだけ不思議な存在だったのでしょう、よくわかんないけど。まさか本当の事(以下に述べる)を言うわけにもいかず、適当にはぐらかしていました。それゆえに色々と周囲の妄想を駆り立てたようで、奇想天外な週末を過ごしているという伝説だけが勝手に作り上げられたような気がします。

　色々と辛い思いもしましたし、精神的にも相当追い詰められた筈なのですが、あの頃の嫌な辛い思い出が時間の経過と共に不思議と消えていっています。辛い記憶だけがピンポイントで脳の海馬のなかで破壊されているかのようです。まあ、無駄な記憶は消去して、これからの為にメモリを確保してくれた方が効率は良いですね。今では楽しかった思い出だけが鮮明に残っています。こう考えてみると、人間の脳って都合よく出来てますね(何かの本で読みましたが、人間の脳には記憶を取捨選択できる機能があるらしいですよ)。

　実は、私は公共交通機関を利用する機会が多いです。バスや列車での移動の際は必ず何らかの専門資料を携帯します。乗り物に揺られながら資料に目を通し、集中力が途切れると車窓から望む風景を楽しみ、また資料に目を通す・・・この繰り返しです。バスや列車を待つ時も読書、一人でレストランに入り、注文が済むと料理が出てくるまで読書(どうせ時間が掛かるから)・・・何かと細切れの時間に読書をする習慣があります。

　この習慣はまさに、前職の頃に身に着けたものなのです。当時は東京都内の在住・在勤でしたから、公共交通機関はとっても充実していました。都心部に出かける事もあれば、全然違うところにも行きました。そんな時、必ずカバンを携帯してその中には気象予測の専門資料をギッシリと？忍ばせて、列車の中で勉強していました。日曜日には近くの図書館(萩山だったかなあ)に通って、気象力学の理論を勉強した事もありました。ひたすら方程式の導出を繰り返して、数式操作のテクニックをマスターしようとしていました。

　勿論、楽しいイベントや夜通しのイベントにも遊びに出かけました(たまには息抜きもしナイト！)。都心部へのお買い物もよく行きました。ＣＡＭＪの会合にもちょこっと？参加しました。あの頃の皆さん、今も元気にしてるかな～。で、もちろんその際の移動手段も列車がメインですから専門資料を携帯しての参加です。あ、イベント中には勉強はしませんよ、念のため。とにかく列車の中ではよく勉強しました。そして、当時は社員寮に住んでいましたので、社員寮ではひたすら数値シミュレーションの研究と半導体設計の勉強(←本業が半導体だったから)でした。それと平行して有料・無料のメールマガジンをピーク時には４本同時連載！、さらにホームページを２本！・・・今の私にはまず無理です！！あの頃は技術は無かったけど、若さあふれる情熱に溢れていたんだなあ・・・不遇の境遇だったから余計にそれを莫大なエネルギーにしていたのかもしれない。

　平日は半導体設計技術者(と言う事にしておこう)として過ごし、休日は気象の勉強や研究をを少しずつ少しずつ積み上げていました。気象庁や民間気象会社に所属するという形を取らなくとも気象に関われるアマチュア気象予報士のあり方を模索していました。当時は、アマチュアならばアマチュアを極めてやろうと言う想いもありました。だから、当時の職場でも自分の休日を赤裸々になんて、言えるわけ無いですよね。

　今はもう、かつてのようにイベントに参加するとか夜通しで遊ぶという事もなくなりました。まず、東京を離れてしまったので(爆)。もうホームページもメールマガジンも縮小して、メールマガジン１本＋ブログ１本になってしまいました。かつての救急めいとの皆さん、お元気ですか？(←この言葉も今ではどれ程の方に通用するのだろうか)

　この当時からは想像も出来ないくらい？今は本当にひっそりと暮らしています。もしかするとＣＡＭＪの中でもすっかり忘れ去られた存在になっているかもしれません。恐ろしい位、地味な生活を送っています(前職時代が派手と言うわけでは無いけれど、そこから比較しても地味と言う事)。

　ちょっと視点を変えて、もし修士課程を修了してから就職せずにそのまま博士課程に進学していたら・・・という事を考えていたりもします。標準で３年、まあ実情に鑑みて４～５年位掛かって博士号取得できたとして２８～２９歳になってしまいます。修士を終えてそのまま博士課程に進学していたら、あのままアカデミックな世界の中で２８～２９歳になり、そこから社会に進むわけですが・・・博士課程ではなく就職を選んだ事で、それまでの世界とは違う４年間を過ごす事ができました。それから転職して現在に至るわけです。気象データ解析技術の研究開発が加速したのは言うまでも無いことです。ＣＡＭＪで表彰されるに至ったのは周知の通りです。確かに、博士課程に行くのも一つの人生ですが、あえて棘の道を進んだ事で色々な経験ができました。決して、資格や学位と言ったハッキリした形ではありませんが、あの時の辛い思いや苦しかった事も私の中では勲章です。

　これまで研究を続けてきた気象解析の基礎技術。ここまでくるのに時間が掛かった。まあ、掛かりすぎたと言う思いも無きにしも非ず。最近は、色々な熱対流や乱流現象の研究を進めております(ようやくその技術的な基盤が整いました)。教科書では２～３行で定性的に片付けられる事も、深く掘り下げるとなかなか奥が深いものですね。

　まあ、「結婚はどうなっている」との周囲の外圧にも負けず、気象監視体制にも負けず、薄給にも負けず(←しつこいっ！)地味な生活を送っていると言う事は、それだけ研究開発に集中しているとも言えるわけで(エ？実際のところは？・・・セイ！セイ！セイ！)、いよいよ満を持しての・・・(謎)

どうして「数値シミュレーション」なのか？

【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843410.html


　最近の研究でニューラルネットワークにＧＰＶを入力する時にちょっとした工夫をする事で(施さなかった場合に比べて)精度が僅かながら向上する？兆しが見えてきました。この仮説は本当にそうなのか？と言った点については更に検証が必要です。また、学習させる範囲についても、色々とコツがあるようです。ニューラルネットワークに気象の学習をさせておりますが、その一連の過程を通じて、人間の側も学習を重ねております。

　ニューラルネットワークの凄いところは入力と出力のパターン(教師信号)をドンドン学習させると、自動的にその入出力関係を分析して、その関係にマッチしたモデルに進化してくれる事だと思います。一度、ニューラルネットワークモデルを構築すれば、後はそのモデル(計算プログラム)を修正する事は無いのです。

　勿論、これは人間の脳も同じ事で、脳の構造は生まれたときからベースは既に出来上がっていて、後は体の成長と共に発育し、情報については実際に色々な経験や勉強を通じて蓄積していくわけです。例えば、さて来年は○○大学を受験するから○○大学入試対応仕様の脳にしようとか言って、こともあろうに自分の脳を取り出してパーツを追加・交換したり・・・極端な話、大脳新皮質のこの部分をこちらのパーツに交換して脳のメモリを強化して、ついでに小脳もこっちの小脳に交換して・・・なんてことはしないですよね。

　もっとも、ニューラルネットワークは人間の脳の構造(神経回路網)の構造を簡略化したものですから、人間の脳構造よりは遥かに単純です。それにしても、この技術を発案した人は凄い。

　さて、気象予測においては様々な計算手法を駆使した数値予報モデルが開発されておりますが、それでもやはり読みきれない現象も少なくありません。精度の向上、と一口に言っても非常に難しい事である、と言う事は言うまでも無い事と思います。

　先日、日本気象学会(←ＣＡＭＪじゃないよ)の「2007年秋季大会講演予稿集」が私の所にも届きました。分厚いのでまだ各テーマの詳細を見きれていませんが、過去の事例検証や大気擾乱等の現象そのものに関する研究が多く、逆に予報に関するテーマが少ないように感じました(もっと言えば、なかなか見当たらない)。それだけ、予測精度の向上は難しいテーマなのでしょう。逆にだからこそ、やりがいのあるテーマなのだと言う事もできます。

　現在、未来の天気はコンピュータによる数値シミュレーションで予測している、という事実は周知の事でしょう。コンピュータによる予測結果も最終的に気象予報士による判断で修正される事で精度をギャランティーするのはこれまでお話してきた通りです。

　しかし、数値シミュレーションはただ未来を予測するためだけにあるのではありません。様々なパラメータの組み合わせを想定して「もしこのような条件が起こればどのような現象が発生するか」と言った仮想実験を行う事ができます。天気図や観測値は既に起こった(＝既知の)現象を表現するものです。逆に言えば、未知の現象を語るものではありません。私達が狙う相手は未来に起こり得る「未知の現象」です。

　既知の現象を数多く分析して局地的な気象特性を解き明かす事は大切です。そして、この過程を通じて得られた知見なり理論、仮説と言ったものが本当に妥当なものであるのかを検証し、裏付けるに当たっては数値シミュレーションはその威力を発揮します。（この場合の数値シミュレーションは物理学の理論に基づくものである事が望ましいでしょう。なぜならば、物理学の理論に基づく根拠があるからです。）

　実況の解析と数値シミュレーションによる検証の連動は、これからの局地気象の数値シミュレーション技術の有効な方向性ではないかと考えています。

　ニューラルネットワークは単純な入出力関係をパターン化した計算ですので、経験的学習に基づく予測計算を行います。一方、熱流体シミュレーションは物理学の理論を基にした計算ですので、物理学の法則に基づく予測計算を行います。天気図等の資料だけでは見えないものを見る、そのようなツールとして数値シミュレーションは有効なのです。予測精度を向上するためには、より深く局地的な気象特性を知らなければなりません。この特性を見出すための技術と、予測するための技術を研究しているのです。

　ようやく少しずつではありますが、一つ一つの研究が形になり始めています。近い将来、学会の講演予稿集に私の論文が掲載する日が来るでしょう。そして、そろそろ気象特性そのものの研究にも取り掛かっていかなければならないなあ・・・と焦りを感じている今日この頃です。(そもそもシミュレーション技術開発の目的がこのような所にあるので・・・)

数値シミュレーションの解析例

【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843387.html


　流体の基礎方程式であるナビエ・ストークス方程式は、非線形偏微分方程式であるため数学的に解くことが難しいのが実状です。これを解いて流体の挙動を明らかにするには、やはり数値解析の助けが必要です。 数値解析、と言いますと大学や企業などのスーパーコンピュータを思い浮かべる方も多いと思いますが、 近年のコンピュータ技術の発展により、最近では身近なパソコンでも３次元の流体現象までを解析できるようになってきました。

１．後方ステップ流れ

　剥離と再付着を伴う流れは、原子炉・ガスタービン・電子機器・電熱装置等多くの装置で認められ、それらの性能をしばしば左右する流れ現象です。後方ステップ流れは、剥離と再付着を同時に実現する最も基本的な流れであり、数値計算の動作確認には優れたテスト・ケースとして多用されています。
　ステップ上方の流入口（左側）から十分発達した壁乱流が入り、後方ステップを通過して剥離を起こし、床面に再付着した後に発達して流出口（右側）に至るケースを想定したシミュレーションを掲載しています。この時の計算領域のサイズはステップ高さhを基準として、流入部流路幅をh（すなわち拡大率は2.0）、ステップより流出部までの距離を30h、スパン方向距離をhにそれぞれ設定しました。



２．ベナール・セル

　有名なベナール・セルのシミュレーションです。ベナール・セルは薄い流体層に対して鉛直方向にある程度のサーマル・グラディエントを印加することによって、内部に規則正しく配列する対流セルが発生します。
　熱対流の体系的な研究は、1900年にフランスのBenardによる実験から始まりました。パラフィン、鯨油などの粘性の高い流体層の下面を一様に加熱すると、加熱された流体は浮力により上昇するため、流体内部に半定常的な細胞状の模様（対流セル）が形成される事があります。各セルの中心付近では上昇流、境界付近では下降流になっています。



３．閉じたキャビティ内の熱流動

　密閉されたキャビティ内の熱流動です。こちらは水平方向にサーマル・グラディエントを印加しました。２つの渦が発生し、回転しながら中央付近に移動していく様子が再現されています。高温部が上方に、低温部が下方にそれぞれ広がる事により、キャビティ内に大きな渦が発生します。



４．安定成層における山越え気流と風下側の乱渦の発生

　画面左側に小さな山があり、左から右に向かう一様な風の流れが生じている場合を想定したシミュレーションです。風下側では地上風が強化される一方、その上空では複雑な乱渦が発生しています。大気の状態おろし風や乾いたフェーンとして観測されることがあります。

離散的な数値データの空間補正処理

【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843379.html


　やれやれ、嵐のような統一地方選挙戦も終わりましたね・・・f(^^;)。残念ながら私は当選できませんが・・・(そもそも立候補してないので無理も無いのです。これで当選したら・・・ワタシもビビル・・・)

　さて、最近の研究紹介ですが今回は「離散的な数値データの空間補正処理」についてです。前回は不規則に配置された数値データを基にそのパラメータの空間分布を推定するものでした。それに対して今度は、規則的な格子状に配置された数値データの変化をより滑らかに補間(補正・内挿)する数値処理の解析技術を研究しています。
　ここで紹介している図は、見て分かると思いますが、左が補正前、右が補正後のデータのイメージ図です。どんな計算方法を使っているのかは敢えて書きません。分かる人は分かる筈。見当もつかない！という方は、自分なりに色々と検討してみると良いでしょう。

　今はインターネットが発達しているので色々な気象データを入手することが出来ます。私が現在行っているのは、これらのデータを如何にして乱流数値シミュレーションやニューロ・モデルに組み込んでいけるのか、延いてはどのように予報に結び付けていくのかという分野です。

　最近はＧＰＶをニューロ・モデルに入力値として与えて、特定地点の降水確率を予報すると言う実験も繰り返していますが、小さな大気現象に伴う降水はそもそもＧＰＶでも捉えきれていないので、ニューロ・モデルでもあまりはっきりとは出てきません。そこで、数値予報図で上空のトラフの動向などを睨みながら検討して、なるほど～～・・・と妙に納得してみたり・・・。

　人間の判断を介さないフル・オートメーション・ウェザー・プレディクト・システムというのはおのずと限界があるのかなぁ・・・。だからと言って気象予報士を大量に投入するとなると、精度向上以前に人件費やら労働形態の諸問題も絡んでくるわけで・・・精度とコストはトレード・オフになるのかもしれません。

　その前に、人間の判断則をモデルに組み込む方法を考えろ！ですか・・・f(^^;)。