【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843373.html
この前の日曜日に新潟市観光文化検定3級(ニイガタ検定)を受験してきました。そして今日はその合格者が発表されました。ちなみに私は・・・合格していました。私は山形県の出身で、新潟県に来て・・・ようやく2年が過ぎようとしています。地域の事をもっと良く知りたいと言う思いがあっただけに良い勉強の機会に恵まれました。考えてみれば、先月上旬には日本漢字能力検定2級を受験しましたので、最近は検定試験ラッシュでした・・・。結局、どちらとも合格できたので、めでたしめでたし・・・と言う事で当分の間、検定試験は受けません(多分)。
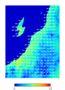
さて、今日も画像を添付しました。前回、アメダス観測値を基にしてメッシュ気候値の分布を求める研究を紹介しましたが、これをさらに発展させようと日々奮闘しています。今回の画像は、日本海低気圧に伴って日中に顕著なフェーン現象が発生した日のアメダス観測値を基に解析したメッシュ毎の気温と風ベクトルの分布図です。時間の経過を表現するためにアニメーションGIF表示にしています。
時間は表示されていませんが、午前中は東~南東よりの風が卓越する一方、夕方になると弱い北西よりの風に変化しています。これは午後に寒冷前線が通過した事に伴うものと考えられます。日中の気温の分布に関しても、日本海沿岸部で顕著な高温域が解析されています。アメダス観測点は不規則に点在していますが、そのデータを基にメッシュ推定解析を行う事で、より詳細な現象特性の把握に役立てることが出来るでしょう。
https://ameblo.jp/qq-otenki-s/entry-12897843373.html
この前の日曜日に新潟市観光文化検定3級(ニイガタ検定)を受験してきました。そして今日はその合格者が発表されました。ちなみに私は・・・合格していました。私は山形県の出身で、新潟県に来て・・・ようやく2年が過ぎようとしています。地域の事をもっと良く知りたいと言う思いがあっただけに良い勉強の機会に恵まれました。考えてみれば、先月上旬には日本漢字能力検定2級を受験しましたので、最近は検定試験ラッシュでした・・・。結局、どちらとも合格できたので、めでたしめでたし・・・と言う事で当分の間、検定試験は受けません(多分)。
さて、今日も画像を添付しました。前回、アメダス観測値を基にしてメッシュ気候値の分布を求める研究を紹介しましたが、これをさらに発展させようと日々奮闘しています。今回の画像は、日本海低気圧に伴って日中に顕著なフェーン現象が発生した日のアメダス観測値を基に解析したメッシュ毎の気温と風ベクトルの分布図です。時間の経過を表現するためにアニメーションGIF表示にしています。
時間は表示されていませんが、午前中は東~南東よりの風が卓越する一方、夕方になると弱い北西よりの風に変化しています。これは午後に寒冷前線が通過した事に伴うものと考えられます。日中の気温の分布に関しても、日本海沿岸部で顕著な高温域が解析されています。アメダス観測点は不規則に点在していますが、そのデータを基にメッシュ推定解析を行う事で、より詳細な現象特性の把握に役立てることが出来るでしょう。