読書ノート R・Pファイマン著 「光と物質の不思議な理論ー私の量子電磁力学」（岩波現代文庫）

光子と電子の相互作用を解き明かす量子電磁力学が描く物理学的世界像 第５回

１）　初めに（確率論の手法） （その３）

ニュートン光学が述べる部分反射を考え直すにあたって、確率統計学が提供する手法の約束事を2つだけ述べます。この手法はほかの物理問題を扱うQEDにおいても重要な方法となります。一つ一つの事象の連続過程（または平衡現象）を→でたどってゆき最終矢印を得ること（矢印の足し算）が基本となります。
①　一つの事象の起る確率は矢印の自乗に等しい。つまり4%ということは0.2という長さの矢印（最終矢印）のことです。16％ということは0.4という長さの矢印のことです。酔歩でいったでたらめの方向を統計的に合算すると最終矢印は（ゼロ）元に戻ることです。
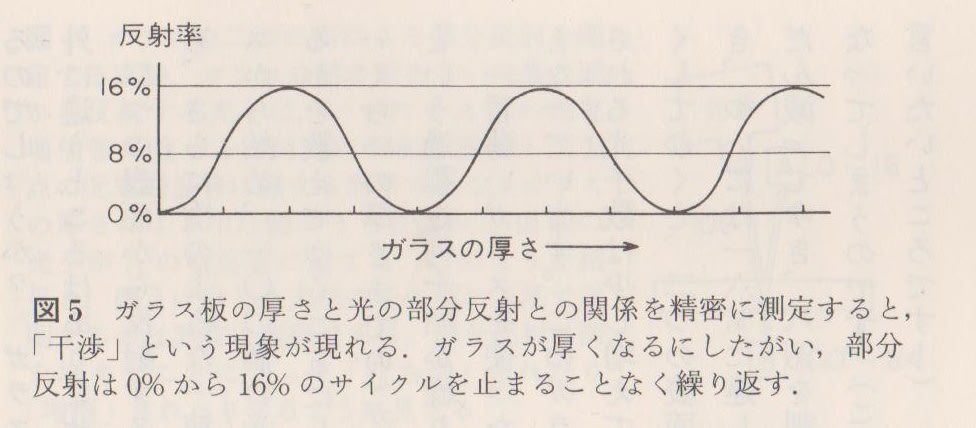
②　想像上の時計の針がまわっていて、針の角度が時間もしくは速度に比例する。そこでガラスの全面で跳ね返る光の時計の針の向きは逆（180度）にむけて描くことです。光の進む方向であれなおなじ向きで→を描き、反射は反対方向に→をむけます。だからガラスの第1面と第2面での反射の合計は、0.2という長さの→（第1面）と0.2という長さの←（第2面）の頭と尻を結んで合成するので、非常に薄いガラス厚みでは針はほとんど進まないので最終矢印の長さはゼロとなります。次第にガラスが厚くなると光の時間（光路）差が出てくるので、→足す←の合成は三角形の1辺となりその辺（合成事象）の長さはガラス厚みとともに変化します。第1事象（第1面での反射）の針は固定すると、第2事象（第2面での反射）の針はガラス厚みとともにくるくる回転します。合成された3角形の1辺が最終矢印となり、その最長の長さは→足す→で、180度の位置で長さは0.2＋0.2＝0.4です。確率は①より0.2×0.2＝0.16（反射率16％）となり、ガラス厚みと連動して反射率は（ゼロを最小とし、16を最大とし、平均を8とする）周期関数となります。またこの矢印は確率論では「事象の確率振幅」と呼びます。つまりある事象の確率振幅を計算していることになります。
この反射の周期現象は、可視光の波長（波動論の波長という言い方をそのまま採用するとして）による分光を行うことになり、虹現象、あるいは油膜現象（シャボン玉）と呼ばれ美しい玉虫色が周期的に現れることを説明しています。下の図に反射確率振幅の手法を示す。

（つづく）