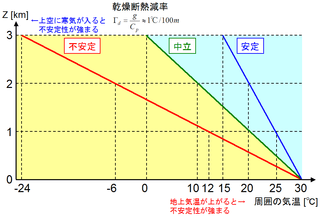
【※】gooブログのサービス終了に伴い、アメーバブログに移転しています。
https://ameblo.jp/qq-otenki-s/entry-12897843654.html
世間はゴールデンウィークのようですが、私には浮かれている余裕はありません・・・。
さて、大気大循環はどうして三細胞構造になるのか ・・・この問題もまた、私にとっては非常に悩ましいものだったので、今回取り上げてみました・・・。

図1.地球放射と太陽放射(上)、地球放射と太陽放射の熱収支(下)
地球放射と太陽放射の関係について図1上に示しました。周知のように地球には太陽からのエネルギーが降り注いでいます(太陽放射)。その一方で地球は外部に向かって常にエネルギーを放出し続けています(地球放射)。
図1下のグラフには地球放射と太陽放射の熱収支を示しました。赤道付近では加熱が進む一方、極地方では冷却が進む事になるので、赤道から極に向かっての熱輸送が行われます。この熱輸送の仕組みとして考えられているのが、これから述べる大気大循環です。

図2.大気大循環の構造
当初は図2(a)のように赤道を熱源、極地方を冷源とした一つの大きな熱対流が起こっていると考えられていました。しかし、実際には図2(b)のような三つの循環からなる三細胞構造だったことがわかってきました。この構造のメカニズムについて、単純化して考えてみましょう。
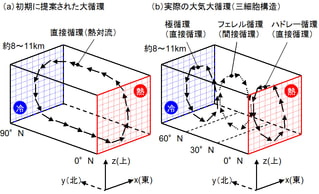
図3.大気大循環の水槽モデル概念図
図2の大気の大循環を、図3のように簡単なモデルに表してみました。水槽の片側を熱源、反対側を冷源としてこの水槽内の鉛直循環を考えるものです。

図4.極循環の形成メカニズム
まずは極循環の形成メカニズムを考えてみます。図4に示したように、当初の考え方によれば、水槽の底面では空気の塊は冷源から熱源に向かって真っ直ぐに進もうとする筈ですが・・・
ここで重要となるのが、コリオリの力です。地球上で運動する物体には、地球の自転に伴ってコリオリの力という慣性力が働きます。いま、物体が速度u[m/s]で運動している場合、コリオリの力は進行方向の右向きに作用し、その大きさは「2Ωusinφ」で表すことができます(Ω:地球の自転の角速度[rad/s]、φ:緯度[°])。
従って、実際にはコリオリの力が働くため、空気塊の軌道は右向きにねじ曲げられていきます。この結果、90°Nからスタートした空気塊の南下はおよそ60°Nまでが限界となり、この範囲に限定した鉛直循環を形成する事になると考えられます。

図5.ハドレー循環の形成メカニズム
続いてハドレー循環の形成メカニズムを考えてみましょう。図5に示したように、当初の考え方によれば、水槽の上面では空気の塊は熱源から冷源に向かって真っ直ぐに進もうとする筈です。しかし、上記と同様に、実際にはコリオリの力が働くため、空気塊の軌道は右向きにねじ曲げられていきます。この結果、0°Nからスタートした空気塊の北上はおよそ30°Nまでが限界となり、この範囲に限定した鉛直循環を形成する事になると考えられます。
以上の極循環とハドレー循環のように力学的なメカニズムで直接的に駆動される循環を直接循環と言います。これに対してフェレル循環のように二つの直接循環に挟まれる事によって結果的に新たな(見せかけの)循環として生じるものを間接循環と呼びます。

https://ameblo.jp/qq-otenki-s/entry-12897843654.html
世間はゴールデンウィークのようですが、私には浮かれている余裕はありません・・・。
さて、大気大循環はどうして三細胞構造になるのか ・・・この問題もまた、私にとっては非常に悩ましいものだったので、今回取り上げてみました・・・。

図1.地球放射と太陽放射(上)、地球放射と太陽放射の熱収支(下)
地球放射と太陽放射の関係について図1上に示しました。周知のように地球には太陽からのエネルギーが降り注いでいます(太陽放射)。その一方で地球は外部に向かって常にエネルギーを放出し続けています(地球放射)。
図1下のグラフには地球放射と太陽放射の熱収支を示しました。赤道付近では加熱が進む一方、極地方では冷却が進む事になるので、赤道から極に向かっての熱輸送が行われます。この熱輸送の仕組みとして考えられているのが、これから述べる大気大循環です。

図2.大気大循環の構造
当初は図2(a)のように赤道を熱源、極地方を冷源とした一つの大きな熱対流が起こっていると考えられていました。しかし、実際には図2(b)のような三つの循環からなる三細胞構造だったことがわかってきました。この構造のメカニズムについて、単純化して考えてみましょう。

図3.大気大循環の水槽モデル概念図
図2の大気の大循環を、図3のように簡単なモデルに表してみました。水槽の片側を熱源、反対側を冷源としてこの水槽内の鉛直循環を考えるものです。

図4.極循環の形成メカニズム
まずは極循環の形成メカニズムを考えてみます。図4に示したように、当初の考え方によれば、水槽の底面では空気の塊は冷源から熱源に向かって真っ直ぐに進もうとする筈ですが・・・
ここで重要となるのが、コリオリの力です。地球上で運動する物体には、地球の自転に伴ってコリオリの力という慣性力が働きます。いま、物体が速度u[m/s]で運動している場合、コリオリの力は進行方向の右向きに作用し、その大きさは「2Ωusinφ」で表すことができます(Ω:地球の自転の角速度[rad/s]、φ:緯度[°])。
従って、実際にはコリオリの力が働くため、空気塊の軌道は右向きにねじ曲げられていきます。この結果、90°Nからスタートした空気塊の南下はおよそ60°Nまでが限界となり、この範囲に限定した鉛直循環を形成する事になると考えられます。

図5.ハドレー循環の形成メカニズム
続いてハドレー循環の形成メカニズムを考えてみましょう。図5に示したように、当初の考え方によれば、水槽の上面では空気の塊は熱源から冷源に向かって真っ直ぐに進もうとする筈です。しかし、上記と同様に、実際にはコリオリの力が働くため、空気塊の軌道は右向きにねじ曲げられていきます。この結果、0°Nからスタートした空気塊の北上はおよそ30°Nまでが限界となり、この範囲に限定した鉛直循環を形成する事になると考えられます。
以上の極循環とハドレー循環のように力学的なメカニズムで直接的に駆動される循環を直接循環と言います。これに対してフェレル循環のように二つの直接循環に挟まれる事によって結果的に新たな(見せかけの)循環として生じるものを間接循環と呼びます。