Ｍ村さんまたしても明察（解答編）

　さて、先週再アップした問題の解答です。
もともと、これは「ラングレーの問題」という、E.M.ラングレーが考案した問題の一つで、幾何学をやる人は多かれ少なかれ挑戦するのだそうです。難問かつシンプルな美しさゆえに好まれるのだとか。それをチョチョイと解いてしまうＭ村さん、やっぱ頼りになるというか、悔しいというか｡｡｡以下、Ｍ村さんの模範解答を紹介します。


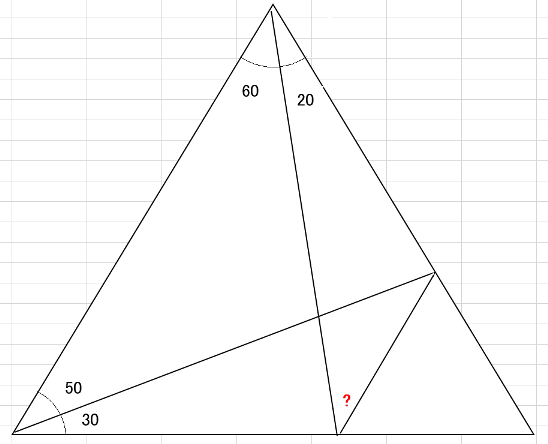
普通に角度を埋めていくだけでは解答が得られず、補助線も思い付かないので、三角形を正しく描く。



簡単なところから角度を埋めていくと、底角５０の二等辺三角形を発見する。



（ここがポイント）辺ａの正三角形の補助線を引いて、角度を埋めていくと、底角40の辺ａの二等辺三角形を発見する。



最後に発見できた頂角40の二等辺三角形の底角は70度。ゆえに、求める角度？は「30度」。



　こんな補助線思いつかんかったわ。今回は、結局Ｍ村さんに教えてもらうまで、私は自力で解けませんでした。降参です。でもやっぱり面白いので、また興味深い問題を見つけたら紹介します。Ｍ村さんありがとうございました。またピンチの時、よろしくお願いします m(_ _)m

Ｍ村さんまたしても明察（改訂版）

問：以下の条件で？の角度を求めよ。



　先日アップして、調整していた設問を再開します。もともとは「ネットで見つけた問題が解けないでいたら、Ｍ村さんがすぐに解いてしまいました」という内容で、その主旨は変わりません。
　上記の図形は見やすくするために角度を誇張してあり、別にこれで解けないわけじゃないのですが、小心者の私はアップ後に「角度が不正確だ」とツッコまれるんじゃないかと心配になり、思案のためいったん非公開にしました。で、一応参考までに、角度を正確に描いた画像も添付します。




　というわけで、この問題を「今勾股弦釣九寸股壱拾弐寸在　内ニ如図等円双ツ入ル　円径ヲ問」という設問の解き方で紹介した宇宙エレベーター協会（JSEA）の仲間・Ｍ村さんは実にあっさり解いてしまいました。Ｍ村さんお見事！(ﾟ∀ﾟ) そんなわけで、次の更新で模範解答を紹介しますので、皆様、よろしければ挑戦してみてください。

年頭あいさつ：軌道の名は。

「うちゅーえれべーたー」ね。その名で呼ぶとは
まだまだお若い (￣▽￣)

　全宇宙に存在するであろう、と思いたい軌道エレベーター派の皆様、あけましておめでとうございます。
軌道エレベーターの分野では、昨年はSTARS-Cが軌道投入されるという画期的イベントがあり、大変喜んでいます｡｡｡が、老若男女問わず「宇宙」「宇宙」と連呼。嬉しくもある一方、情けないやら悔しいやら、愛憎半ばするとはこのことか。

　冒頭のように強気に出られたらありがたいのですが、元の体に戻った後の瀧と三葉のように、みんな「軌道」の名を易々と忘れてゆく。「軌道エレベーター」と呼んでた人たちははどこへ行ってしまったのでしょうか？ いやマジで！ もう過激な手段に出て政府にでも要求するしかないのか？
　みんな「軌道」って掌に油性ペンで書いとけ！ ( ﾟдﾟ )ｸﾜｯ

前回目次に掲載したやつの続きです↓


　このような状況ですが、「軌道」の名が忘れ去られないよう、は今年も闘い続けます。皆様、本年もよろしくお願いいたします。
　以下は、毎年恒例のまとめ目次です。末尾のリンクから前回の目次、そこからさらに前の目次へとたどれるようになっています。　

目次（2016年４～12月）
前回の目次からきょうまでに更新がなかったコーナーについては、一番最近の記事を載せています。

軌道エレベーター派宣言
　あいさつに代えて、このホームページのスローガンのご披露

軌道エレベーター早わかり
　はじめて「軌道エレベーター」という言葉を知った方のための、簡単な基礎知識の説明

（軌道派による軌道派のための）軌道エレベーター定義書
　当サイトにおける「軌道エレベーター」の構造や分類などについてまとめた定義一覧

軌道エレベーター豆知識
　軌道エレベーターに関する情報や知識をテーマ別に紹介
(31)時間の遅れ

軌道エレベーターが登場するお話
　小説や映画、アニメなど、軌道エレベーターに関係する創作のあらすじと、作中に登場する軌道エレベーターの特徴の解説
(14) ミスター・ノーバディ
(15) 通天閣発掘＆果しなき流れの果に･補足

専門書・論文レビュー
　軌道エレベーター関連書や論文の紹介
　(７) 大林組「宇宙エレベーター建設構想」

軌道派アイデアノート
　軌道エレベーターに関する管理人のオリジナルアイデアの紹介
　(4) デブリ根絶計画(上)
　(4) デブリ根絶計画(中)
　(4) デブリ根絶計画(下)

軌道エレベーター学会
　軌道エレベーターに関する研究発表
　軌道エレベーターによる放射性廃棄物の処分（改訂版）序文と目次
　I章　軌道エレベーターの可能性
　II章　放射性廃棄物処分の現状
　III章 軌道エレベーターによる放射性廃棄物の処分
　IV章 処分計画の改良・応用例
　脚注・参考文献

ニュース
　独自取材のストレートニュース
5.29「宇宙エレベーター学会（JpSEC）開催」
10.2「宇科連で九つの軌道エレベーター関連の発表」
12.1「第８回『宇宙エレベーターチャレンジ』（SPEC016）水戸市で開催」12.11「軌道エレベーター実験衛星『STARS-C』打ち上げ」
12.28「（解説）STARS-Cのミッションと意義」


その他の雑記
　テーマにこだわらない、日々の他愛のない感想や雑学メモなど
4.14「君は『超ムーの世界』をみたか」
5.1「地震予知を宇宙から」
5.18「近況報告」
6.4「JSEA理事に復帰しました」
6.19「2016年ＮＨＫ熱中症予防情報 速報」
7.16「毎年７月31日は『軌道エレベーターの日』」
7.31「きょうは軌道エレベーターの日」
8.1「『軌道エレベーターの日』プレゼント当選者発表」
12.7「スランプの時は」
12.31「よいお年を」

　これより前の目次は、今年１月１日の更新の雑記4.3「７周年」（前回の目次も兼ねています）をご覧ください。その目次からさらに前の目次の回へとたどれるようになっています。