PasocomMini PC-8001活用のZOMETOOLの確認ソフト計画。
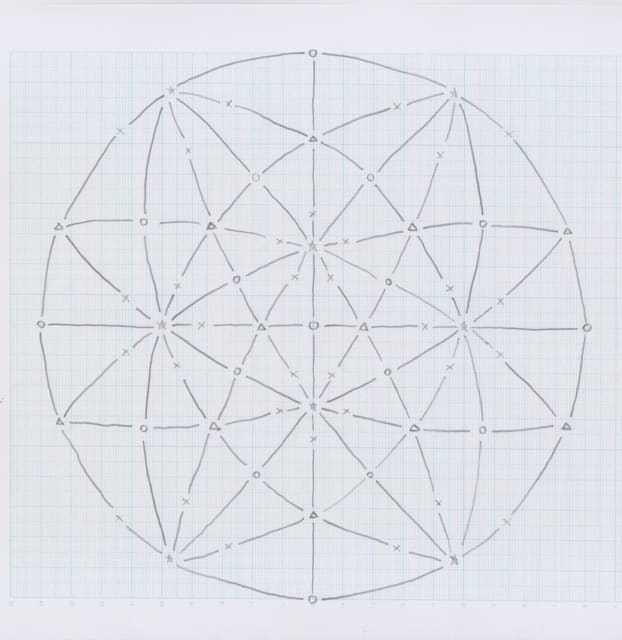
ZOMEボールの穴の方向を計算するために、図を描いて見ました。下にスキャンしたものが見えると思います。見れば分かるように、方眼紙に手書きしました。もっと丁寧に描けよ、との感想の方もおられると思いますが、この程度で十分に役立ちます。
幾何学に普段から関心のある方なら、ああ、これは正20面体の対称性の図だ、と直感すると思います。図は半球を示したもので、△が正20面体の正三角形の面の中心位置、☆が頂点で、正12面体を表すときはここが正五角形の面の中心になります。○は稜の中点です。
平射図法を用いていて、つまり南極点から透明な地球の北半球を見て、赤道面のスクリーンに投射した感じ。正射図法ではありません。中心から周辺に行くに従い拡大されていて、赤道面では2倍になっています。その代わりとして、これは等角写像になっていて、角度が保存されます。小さな三角形☆△○はすべて合同な球面直角三角形です。見れば分かるように、∠△○☆が90°、∠☆△○が60°、∠○☆△が36°です。
×は何かというと、ZOMETOOLの緑棒の方向です。☆から△に向かう直線(測地線)上、すぐの所にあります。○が青棒の穴、△が黄棒の穴、☆が赤棒の穴で、穴の形は×の位置で想像できると思います。
平射図法では測地線、つまり赤道や子午線などの大円は直線または円に写像されます。正20面体の対称性では15本の対称線の大円が球面を覆っていて、その全てが見えています。
さて、座標計算ですから座標を導入する必要があります。地球に見立てると、真ん中の○が北極で、北緯90°。右端の○が経度0、緯度0。上端の○が東経90°緯度0とします。ですから図の外縁の円は赤道に相当します。
つまり言いたいのは、球の中心に原点(0, 0, 0)があり(座標(x, y, z)でx=0, y=0, z=0)、図の右に向かってx軸があって、右端の○の座標が(1, 0, 0)、図の上に向かってy軸があって上端の○の座標が(0, 1, 0)、図のこちら側に向かってz軸があって中央の○の座標が(0, 0, 1)。つまり円形ドームを上から見た感じになります。以下、この球の中心を◎で表すこととします。
北極から見下ろしているのですから、中央の○と中心の◎は重なってしまっています。
右端の○から赤道の円に沿って上端の○まで、○△×☆○と記号が続いています。
この中で名前が付いている中心角は、
λ = ∠○◎☆ = (1/2)arctan(2) = 約31.717° = 約0.5536rad
μ = ∠○◎△ = (1/2)arcsin(2/3) = (1/2)arctan(2/√5)
= 約20.905° = 約0.3649rad
の2つで、arctanは逆正接関数、arcsinは逆正弦関数、radは弧度法の角度のラジアンです。表計算ソフトなどでは角度は°ではなくラジアンで表示されるので添えました。
緑棒の中心角は単純で、∠○◎×は45°です。
ですから、図の右上方向の赤道上の点の座標は簡単で、☆は(sin λ、cos λ、0)、△は(cos μ、sin μ、0)で、表計算ソフトでもN-BASICでも答え一発です。地図のx軸上、y軸上(つまり図の横と縦の直線)に乗っている点も同様に簡単。残りは四分円の内点ですが、△は実は中央の○、右端の○、上端の○の3直角球面三角形の中心なので、(1/√3、1/√3、1/√3)と、ただちに計算できます。
…、長くなりそうなので、多分、続く。