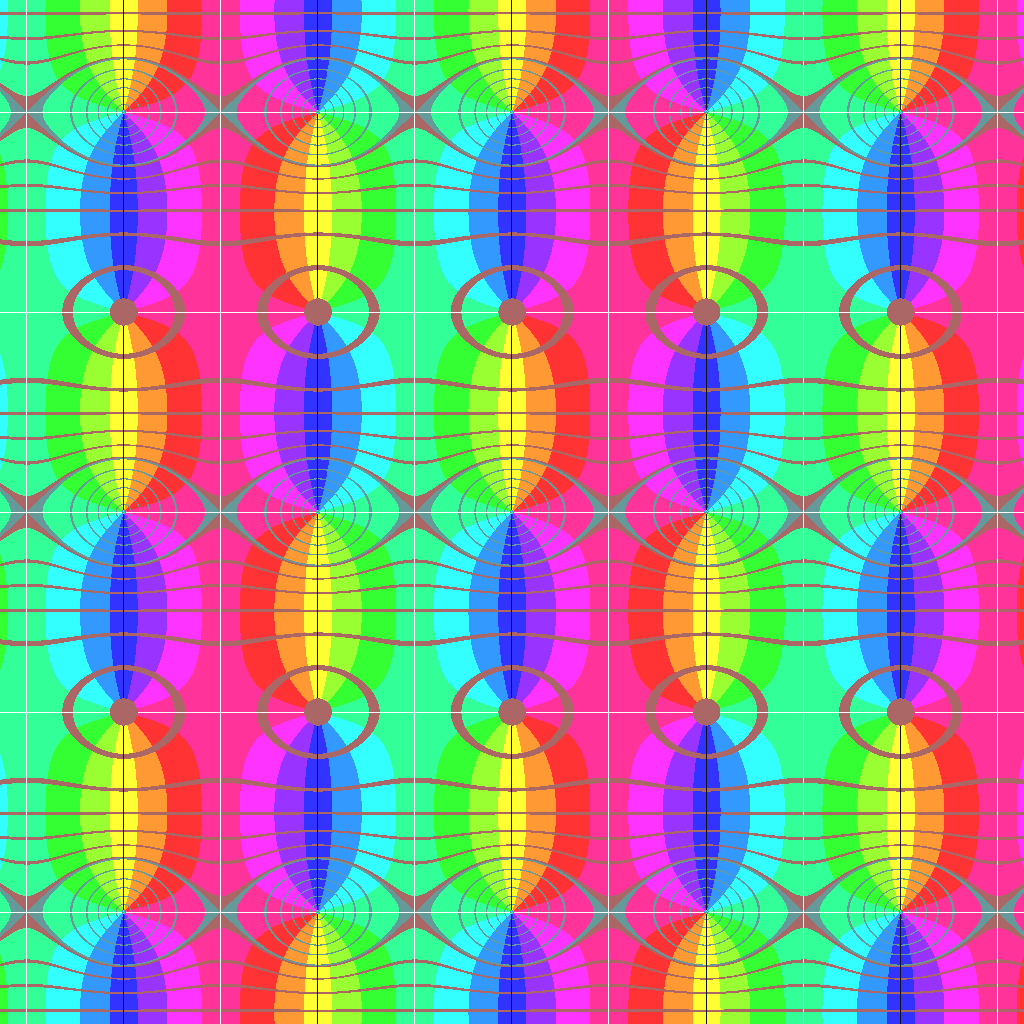
今回作成した、ヤコビの楕円関数の複素平面表示のプログラムです。適当なコンパイラでコンパイルし、実行するとグラフの3ファイル、sn.bmp, cn.bmp, dn.bmpがソースプログラムのあるフォルダに出力されます。同時に、グラフを読むのに必要な数値をまとめたテキストファイル、el.txtが出力されます。(230811改訂版)
// ConsoleApplication7.cpp
// ellptic3.cpp; Jacobi elliptic functions on a Gaussian plane
// based on bmp24.cpp
// 200828; making 24bit color bmp file
// 230711; 230722; 230729; 230811
#include <stdio.h>
#include <math.h>
const int WT = 1024; // width (mod 8 = 0) *** modify here
const int HT = 1024; // height (mod 8 = 0) *** modify here
const int BZ = WT * HT * 3; // buffer size
const int FZ = BZ + 0x36; // file size
unsigned char b1[0x36]; // header*2
unsigned char b2[BZ]; // bitmap sn
unsigned char b3[BZ]; // bitmap cn
unsigned char b4[BZ]; // bitmap dn
const double pi4 = atan(1.0);
// elliptic k (0.0 <= k <= 1.0)
double elk = sqrt(0.9755); // k^2: ***modify here
// draw area definition *** modify here
// UD,VD will be automatically modified with K'/K
const double UC = 0.00125; // real base
const double VC = 0.00125; // imaginary base
double UD = 0.0025; // real pitch // hard
double VD = 0.0025; // imaginary pitch // hard
// contour information *** modify here
const double DD = pi4 * 15.0 / 90.0; // value hight pitch
const double DE = 0.125; // value edge width (0.01 - 0.99)
// pole area definition *** modify here
const double anp = tan(4.0 * pi4 / 90.0); // pole area (infinity) in degree
const double asp = tan(4.0 * pi4 / 90.0); // zero point area in degree
// Riemann sphere magnitude (absolute value at equator)
// it dose not adjusted by 1/k or k'/k or k'. please rewrite manually
// const double alf = sqrt(1.0 - elk * elk) / elk; // example
const double alf = 1.0; // *** modify here
// color index
const unsigned char cl0[7][3] = { // {b, g, r} 0-255
{ 0x2e, 0x2e, 0x2e }, // background
{ 0x66, 0x66, 0xbb }, // pole (infinity)
{ 0xbb, 0xbb, 0x22 }, // zero point
{ 0x11, 0x11, 0x11 }, // real part = 0; pure imaginary
{ 0xff, 0xff, 0xff }, // imaginary part = 0; pure real
{ 0x66, 0x66, 0xaa }, // contour edge nothern hemisphere
{ 0x99, 0x99, 0x66 } // contour edge southern hemisphere
};
const unsigned char cl1[24][3] = {
{ 0x99, 0xff, 0x33 },{ 0xff, 0xff, 0x33 },{ 0xff, 0xff, 0x33 },{ 0xff, 0x99, 0x33 },
{ 0xff, 0x99, 0x33 },{ 0xff, 0x33, 0x33 },{ 0xff, 0x33, 0x33 },{ 0xff, 0x33, 0x99 },
{ 0xff, 0x33, 0x99 },{ 0xff, 0x33, 0xff },{ 0xff, 0x33, 0xff },{ 0x99, 0x33, 0xff },
{ 0x99, 0x33, 0xff },{ 0x33, 0x33, 0xff },{ 0x33, 0x33, 0xff },{ 0x33, 0x99, 0xff },
{ 0x33, 0x99, 0xff },{ 0x33, 0xff, 0xff },{ 0x33, 0xff, 0xff },{ 0x33, 0xff, 0x99 },
{ 0x33, 0xff, 0x99 },{ 0x33, 0xff, 0x33 },{ 0x33, 0xff, 0x33 },{ 0x99, 0xff, 0x33 }
};
// elliptic function constants
double elq, elqc; // q, q'
double elkc, ellk, ellkc; // k', K, K'
double te2a, te3a, te0a, tf2a, tf3a, tf0a; // theta(0)s
// elliptic function lines
double te1[WT + 1], te2[WT + 1], te3[WT + 1], te0[WT + 1]; // using q
double tf1[HT + 1], tf2[HT + 1], tf3[HT + 1], tf0[HT + 1]; // using q'
// elliptic function buffers
double tea[WT + 1], teb[WT + 1], tfa[HT + 1], tfb[HT + 1]; // denominator: sn0 = cn0 = dn0
void init1(void) {
int i;
double u;
// prepare constants
double ell = (1.0 - pow(1.0 - elk * elk, 0.25)) / 2.0 / (1.0 + pow(1.0 - elk * elk, 0.25));
elq = ell + 2.0 * pow(ell, 5.0) + 15.0 * pow(ell, 9.0) + 150.0 * pow(ell, 13.0) + 1707.0 * pow(ell, 17.0);
// elq = 0.04321; // starting with q
te2a = 2.0 * (pow(elq, 0.25) + pow(elq, 2.25) + pow(elq, 6.25) + pow(elq, 12.25) + pow(elq, 20.25)
+ pow(elq, 30.25) + pow(elq, 42.25) + pow(elq, 56.25) + pow(elq, 72.25) + pow(elq, 90.25));
te3a = 1.0 + 2.0 * (elq + pow(elq, 4.0) + pow(elq, 9.0) + pow(elq, 16.0) + pow(elq, 25.0)
+ pow(elq, 36.0) + pow(elq, 49.0) + pow(elq, 64.0) + pow(elq, 81.0) + pow(elq, 100.0));
te0a = 1.0 + 2.0 * (-elq + pow(elq, 4.0) - pow(elq, 9.0) + pow(elq, 16.0) - pow(elq, 25.0)
+ pow(elq, 36.0) - pow(elq, 49.0) + pow(elq, 64.0) - pow(elq, 81.0) + pow(elq, 100.0));
elqc = exp(pi4 * pi4 * 16.0 / log(elq));
tf2a = 2.0 * (pow(elqc, 0.25) + pow(elqc, 2.25) + pow(elqc, 6.25) + pow(elqc, 12.25) + pow(elqc, 20.25)
+ pow(elqc, 30.25) + pow(elqc, 42.25) + pow(elqc, 56.25) + pow(elqc, 72.25) + pow(elqc, 90.25));
tf3a = 1.0 + 2.0 * (elqc + pow(elqc, 4.0) + pow(elqc, 9.0) + pow(elqc, 16.0) + pow(elqc, 25.0)
+ pow(elqc, 36.0) + pow(elqc, 49.0) + pow(elqc, 64.0) + pow(elqc, 81.0) + pow(elqc, 100.0));
tf0a = 1.0 + 2.0 * (-elqc + pow(elqc, 4.0) - pow(elqc, 9.0) + pow(elqc, 16.0) - pow(elqc, 25.0)
+ pow(elqc, 36.0) - pow(elqc, 49.0) + pow(elqc, 64.0) - pow(elqc, 81.0) + pow(elqc, 100.0));
elk = pow(te2a / te3a, 2.0); elkc = pow(te0a / te3a, 2.0);
ellk = 2.0 * pi4 * pow(te3a, 2.0); // K
ellkc = ellk / (4.0 * pi4) * log(1 / elq); // K'
// automatic expansion
if (ellk > ellkc) { VD *= ellk / ellkc; }
else { UD *= ellkc / ellk; }
// prepare lines
for (i = 0; i <= WT; i++) {
u = UC + UD * (double)(i - WT / 2);
te1[i] = 2 * (pow(elq, 0.25) * sin(pi4 * 4.0 * u) - pow(elq, 2.25) * sin(pi4 * 4.0 * 3.0 * u)
+ pow(elq, 6.25) * sin(pi4 * 4.0 * 5.0 * u) - pow(elq, 12.25) * sin(pi4 * 4.0 * 7.0 * u)
+ pow(elq, 20.25) * sin(pi4 * 4.0 * 9.0 * u) - pow(elq, 30.25) * sin(pi4 * 4.0 * 11.0 * u)
+ pow(elq, 42.25) * sin(pi4 * 4.0 * 13.0 * u) - pow(elq, 56.25) * sin(pi4 * 4.0 * 15.0 * u)
+ pow(elq, 72.25) * sin(pi4 * 4.0 * 17.0 * u) - pow(elq, 90.25) * sin(pi4 * 4.0 * 19.0 * u));
te2[i] = 2 * (pow(elq, 0.25) * cos(pi4 * 4.0 * u) + pow(elq, 2.25) * cos(pi4 * 4.0 * 3.0 * u)
+ pow(elq, 6.25) * cos(pi4 * 4.0 * 5.0 * u) + pow(elq, 12.25) * cos(pi4 * 4.0 * 7.0 * u)
+ pow(elq, 20.25) * cos(pi4 * 4.0 * 9.0 * u) + pow(elq, 30.25) * cos(pi4 * 4.0 * 11.0 * u)
+ pow(elq, 42.25) * cos(pi4 * 4.0 * 13.0 * u) + pow(elq, 56.25) * cos(pi4 * 4.0 * 15.0 * u)
+ pow(elq, 72.25) * cos(pi4 * 4.0 * 17.0 * u) + pow(elq, 90.25) * cos(pi4 * 4.0 * 19.0 * u));
te3[i] = 1.0 + 2.0 * (elq * cos(pi4 * 8.0 * u) + pow(elq, 4.0) * cos(pi4 * 8.0 * 2.0 * u)
+ pow(elq, 9.0) * cos(pi4 * 8.0 * 3.0 * u) + pow(elq, 16.0) * cos(pi4 * 8.0 * 4.0 * u)
+ pow(elq, 25.0) * cos(pi4 * 8.0 * 5.0 * u) + pow(elq, 36.0) * cos(pi4 * 8.0 * 6.0 * u)
+ pow(elq, 49.0) * cos(pi4 * 8.0 * 7.0 * u) + pow(elq, 64.0) * cos(pi4 * 8.0 * 8.0 * u)
+ pow(elq, 81.0) * cos(pi4 * 8.0 * 9.0 * u) + pow(elq, 100.0) * cos(pi4 * 8.0 * 10.0 * u));
te0[i] = 1.0 + 2.0 * (-elq * cos(pi4 * 8.0 * u) + pow(elq, 4.0) * cos(pi4 * 8.0 * 2.0 * u)
- pow(elq, 9.0) * cos(pi4 * 8.0 * 3.0 * u) + pow(elq, 16.0) * cos(pi4 * 8.0 * 4.0 * u)
- pow(elq, 25.0) * cos(pi4 * 8.0 * 5.0 * u) + pow(elq, 36.0) * cos(pi4 * 8.0 * 6.0 * u)
- pow(elq, 49.0) * cos(pi4 * 8.0 * 7.0 * u) + pow(elq, 64.0) * cos(pi4 * 8.0 * 8.0 * u)
- pow(elq, 81.0) * cos(pi4 * 8.0 * 9.0 * u) + pow(elq, 100.0) * cos(pi4 * 8.0 * 10.0 * u));
}
for (i = 0; i <= HT; i++) {
u = VC + VD * (double)(i - HT / 2);
tf1[i] = 2.0 * (pow(elqc, 0.25) * sin(pi4 * 4.0 * u) - pow(elqc, 2.25) * sin(pi4 * 4.0 * 3.0 * u)
+ pow(elqc, 6.25) * sin(pi4 * 4.0 * 5.0 * u) - pow(elqc, 12.25) * sin(pi4 * 4.0 * 7.0 * u)
+ pow(elqc, 20.25) * sin(pi4 * 4.0 * 9.0 * u) - pow(elqc, 30.25) * sin(pi4 * 4.0 * 11.0 * u)
+ pow(elqc, 42.25) * sin(pi4 * 4.0 * 13.0 * u) - pow(elqc, 56.25) * sin(pi4 * 4.0 * 15.0 * u)
+ pow(elqc, 72.25) * sin(pi4 * 4.0 * 17.0 * u) - pow(elqc, 90.25) * sin(pi4 * 4.0 * 19.0 * u));
tf2[i] = 2.0 * (pow(elqc, 0.25) * cos(pi4 * 4.0 * u) + pow(elqc, 2.25) * cos(pi4 * 4.0 * 3.0 * u)
+ pow(elqc, 6.25) * cos(pi4 * 4.0 * 5.0 * u) + pow(elqc, 12.25) * cos(pi4 * 4.0 * 7.0 * u)
+ pow(elqc, 20.25) * cos(pi4 * 4.0 * 9.0 * u) + pow(elqc, 30.25) * cos(pi4 * 4.0 * 11.0 * u)
+ pow(elqc, 42.25) * cos(pi4 * 4.0 * 13.0 * u) + pow(elqc, 56.25) * cos(pi4 * 4.0 * 15.0 * u)
+ pow(elqc, 72.25) * cos(pi4 * 4.0 * 17.0 * u) + pow(elqc, 90.25) * cos(pi4 * 4.0 * 19.0 * u));
tf3[i] = 1.0 + 2.0 * (elqc * cos(pi4 * 8.0 * u) + pow(elqc, 4.0) * cos(pi4 * 8.0 * 2.0 * u)
+ pow(elqc, 9.0) * cos(pi4 * 8.0 * 3.0 * u) + pow(elqc, 16.0) * cos(pi4 * 8.0 * 4.0 * u)
+ pow(elqc, 25.0) * cos(pi4 * 8.0 * 5.0 * u) + pow(elqc, 36.0) * cos(pi4 * 8.0 * 6.0 * u)
+ pow(elqc, 49.0) * cos(pi4 * 8.0 * 7.0 * u) + pow(elqc, 64.0) * cos(pi4 * 8.0 * 8.0 * u)
+ pow(elqc, 81.0) * cos(pi4 * 8.0 * 9.0 * u) + pow(elqc, 100.0) * cos(pi4 * 8.0 * 10.0 * u));
tf0[i] = 1.0 + 2.0 * (-elqc * cos(pi4 * 8.0 * u) + pow(elqc, 4.0) * cos(pi4 * 8.0 * 2.0 * u)
- pow(elqc, 9.0) * cos(pi4 * 8.0 * 3.0 * u) + pow(elqc, 16.0) * cos(pi4 * 8.0 * 4.0 * u)
- pow(elqc, 25.0) * cos(pi4 * 8.0 * 5.0 * u) + pow(elqc, 36.0) * cos(pi4 * 8.0 * 6.0 * u)
- pow(elqc, 49.0) * cos(pi4 * 8.0 * 7.0 * u) + pow(elqc, 64.0) * cos(pi4 * 8.0 * 8.0 * u)
- pow(elqc, 81.0) * cos(pi4 * 8.0 * 9.0 * u) + pow(elqc, 100.0) * cos(pi4 * 8.0 * 10.0 * u));
}
// prepare denominator
for (i = 0; i <= WT; i++) {
tea[i] = te1[i] * te1[i];
teb[i] = te0[i] * te0[i];
}
for (i = 0; i <= HT; i++) {
tfa[i] = tf1[i] * tf1[i];
tfb[i] = tf2[i] * tf2[i];
}
}
void drawsn1(unsigned char** pp, int i, int j) {
double sn1, sn2, sn0;
double z;
int k;
sn0 = tea[i] * tfa[j] + teb[i] * tfb[j];
sn1 = elkc / elk * te1[i] * te0[i] * tf3[j] * tf0[j];
sn2 = elkc / elk * te2[i] * te3[i] * tf1[j] * tf2[j];
z = sqrt(sn1 * sn1 + sn2 * sn2);
if (sn0 < 1e-10) { // pole
*(*pp)++ = cl0[1][0]; *(*pp)++ = cl0[1][1]; *(*pp)++ = cl0[1][2];
return;
}
if (z < 1e-10) { // zero point
*(*pp)++ = cl0[2][0]; *(*pp)++ = cl0[2][1]; *(*pp)++ = cl0[2][2];
return;
}
if (z / sn0 / alf < asp) { // south pole area
*(*pp)++ = cl0[2][0]; *(*pp)++ = cl0[2][1]; *(*pp)++ = cl0[2][2];
return;
}
if (sn0 / z * alf < anp) { // north pole area
*(*pp)++ = cl0[1][0]; *(*pp)++ = cl0[1][1]; *(*pp)++ = cl0[1][2];
return;
}
if (sn1 * (te1[i + 1] * te0[i + 1] * tf3[j] * tf0[j]) <= 0) { // pure imaginary
*(*pp)++ = cl0[3][0]; *(*pp)++ = cl0[3][1]; *(*pp)++ = cl0[3][2];
return;
}
if (sn1 * (te1[i] * te0[i] * tf3[j + 1] * tf0[j + 1]) <= 0) { // pure imaginary
*(*pp)++ = cl0[3][0]; *(*pp)++ = cl0[3][1]; *(*pp)++ = cl0[3][2];
return;
}
if (sn2 * (te2[i + 1] * te3[i + 1] * tf1[j] * tf2[j]) <= 0) { // pure real
*(*pp)++ = cl0[4][0]; *(*pp)++ = cl0[4][1]; *(*pp)++ = cl0[4][2];
return;
}
if (sn2 * (te2[i] * te3[i] * tf1[j + 1] * tf2[j + 1]) <= 0) { // pure real
*(*pp)++ = cl0[4][0]; *(*pp)++ = cl0[4][1]; *(*pp)++ = cl0[4][2];
return;
}
z = atan(z / alf / sn0) - pi4; // -pi/4 <= z < pi/4
if ((z > 0.0) && (fmod(z, DD) <= DE * DD)) { // north edge
*(*pp)++ = cl0[5][0]; *(*pp)++ = cl0[5][1]; *(*pp)++ = cl0[5][2];
return;
}
if ((z <= 0.0) && (fmod(-z, DD) <= DE * DD)) { // south edge
*(*pp)++ = cl0[6][0]; *(*pp)++ = cl0[6][1]; *(*pp)++ = cl0[6][2];
return;
}
k = (int)((atan2(sn2, sn1) / pi4) * 2.999 + 12.0); // hard
*(*pp)++ = cl1[k][0]; *(*pp)++ = cl1[k][1]; *(*pp)++ = cl1[k][2];
}
void drawcn1(unsigned char** pp, int i, int j) {
double cn1, cn2, cn0;
double z;
int k;
cn0 = tea[i] * tfa[j] + teb[i] * tfb[j];
cn1 = elkc / elk * te2[i] * te0[i] * tf2[j] * tf0[j];
cn2 = -elkc / elk * te1[i] * te3[i] * tf1[j] * tf3[j];
z = sqrt(cn1 * cn1 + cn2 * cn2);
if (cn0 < 1e-10) { // pole
*(*pp)++ = cl0[1][0]; *(*pp)++ = cl0[1][1]; *(*pp)++ = cl0[1][2];
return;
}
if (z < 1e-10) { // zero point
*(*pp)++ = cl0[2][0]; *(*pp)++ = cl0[2][1]; *(*pp)++ = cl0[2][2];
return;
}
if (z / cn0 / alf < asp) { // south pole area
*(*pp)++ = cl0[2][0]; *(*pp)++ = cl0[2][1]; *(*pp)++ = cl0[2][2];
return;
}
if (cn0 / z * alf < anp) { // north pole area
*(*pp)++ = cl0[1][0]; *(*pp)++ = cl0[1][1]; *(*pp)++ = cl0[1][2];
return;
}
if (cn1 * (te2[i + 1] * te0[i + 1] * tf2[j] * tf0[j]) <= 0) { // pure imaginary
*(*pp)++ = cl0[3][0]; *(*pp)++ = cl0[3][1]; *(*pp)++ = cl0[3][2];
return;
}
if (cn1 * (te2[i] * te0[i] * tf2[j + 1] * tf0[j + 1]) <= 0) { // pure imaginary
*(*pp)++ = cl0[3][0]; *(*pp)++ = cl0[3][1]; *(*pp)++ = cl0[3][2];
return;
}
if (cn2 * (-te1[i + 1] * te3[i + 1] * tf1[j] * tf3[j]) <= 0) { // pure real
*(*pp)++ = cl0[4][0]; *(*pp)++ = cl0[4][1]; *(*pp)++ = cl0[4][2];
return;
}
if (cn2 * (-te1[i] * te3[i] * tf1[j + 1] * tf3[j + 1]) <= 0) { // pure real
*(*pp)++ = cl0[4][0]; *(*pp)++ = cl0[4][1]; *(*pp)++ = cl0[4][2];
return;
}
z = atan(z / alf / cn0) - pi4; // -pi/4 <= z < pi/4
if ((z > 0.0) && (fmod(z, DD) <= DE * DD)) { // north edge
*(*pp)++ = cl0[5][0]; *(*pp)++ = cl0[5][1]; *(*pp)++ = cl0[5][2];
return;
}
if ((z <= 0.0) && (fmod(-z, DD) <= DE * DD)) { // south edge
*(*pp)++ = cl0[6][0]; *(*pp)++ = cl0[6][1]; *(*pp)++ = cl0[6][2];
return;
}
k = (int)((atan2(cn2, cn1) / pi4) * 2.999 + 12.0); // hard
*(*pp)++ = cl1[k][0]; *(*pp)++ = cl1[k][1]; *(*pp)++ = cl1[k][2];
}
void drawdn1(unsigned char** pp, int i, int j) {
double dn1, dn2, dn0;
double z;
int k;
dn0 = tea[i] * tfa[j] + teb[i] * tfb[j];
dn1 = elkc * te3[i] * te0[i] * tf2[j] * tf3[j];
dn2 = -elkc * te1[i] * te2[i] * tf1[j] * tf0[j];
z = sqrt(dn1 * dn1 + dn2 * dn2);
if (dn0 < 1e-10) { // pole
*(*pp)++ = cl0[1][0]; *(*pp)++ = cl0[1][1]; *(*pp)++ = cl0[1][2];
return;
}
if (z < 1e-10) { // zero point
*(*pp)++ = cl0[2][0]; *(*pp)++ = cl0[2][1]; *(*pp)++ = cl0[2][2];
return;
}
if (z / dn0 / alf < asp) { // south pole area
*(*pp)++ = cl0[2][0]; *(*pp)++ = cl0[2][1]; *(*pp)++ = cl0[2][2];
return;
}
if (dn0 / z * alf < anp) { // north pole area
*(*pp)++ = cl0[1][0]; *(*pp)++ = cl0[1][1]; *(*pp)++ = cl0[1][2];
return;
}
if (dn1 * (te3[i + 1] * te0[i + 1] * tf2[j] * tf3[j]) <= 0) { // pure imaginary
*(*pp)++ = cl0[3][0]; *(*pp)++ = cl0[3][1]; *(*pp)++ = cl0[3][2];
return;
}
if (dn1 * (te3[i] * te0[i] * tf2[j + 1] * tf3[j + 1]) <= 0) { // pure imaginary
*(*pp)++ = cl0[3][0]; *(*pp)++ = cl0[3][1]; *(*pp)++ = cl0[3][2];
return;
}
if (dn2 * (-te1[i + 1] * te2[i + 1] * tf1[j] * tf0[j]) <= 0) { // pure real
*(*pp)++ = cl0[4][0]; *(*pp)++ = cl0[4][1]; *(*pp)++ = cl0[4][2];
return;
}
if (dn2 * (-te1[i] * te2[i] * tf1[j + 1] * tf0[j + 1]) <= 0) { // pure real
*(*pp)++ = cl0[4][0]; *(*pp)++ = cl0[4][1]; *(*pp)++ = cl0[4][2];
return;
}
z = atan(z / alf / dn0) - pi4; // -pi/4 <= z < pi/4
if ((z > 0.0) && (fmod(z, DD) <= DE * DD)) { // north edge
*(*pp)++ = cl0[5][0]; *(*pp)++ = cl0[5][1]; *(*pp)++ = cl0[5][2];
return;
}
if ((z <= 0.0) && (fmod(-z, DD) <= DE * DD)) { // south edge
*(*pp)++ = cl0[6][0]; *(*pp)++ = cl0[6][1]; *(*pp)++ = cl0[6][2];
return;
}
k = (int)((atan2(dn2, dn1) / pi4) * 2.999 + 12.0); // hard
*(*pp)++ = cl1[k][0]; *(*pp)++ = cl1[k][1]; *(*pp)++ = cl1[k][2];
}
void draw1(void) {
int i, j;
unsigned char* p2, *p3, *p4;
p2 = b2; p3 = b3; p4 = b4;
for (j = 0; j < HT; j++) {
for (i = 0; i < WT; i++) {
drawsn1(&p2, i, j);
drawcn1(&p3, i, j);
drawdn1(&p4, i, j);
}
}
}
int main()
{
FILE* ftp;
errno_t err;
unsigned int ui;
double z;
// writing hedder
b1[0x00] = 'B'; b1[0x01] = 'M';
b1[0x02] = FZ & 0xff; b1[0x03] = FZ >> 8 & 0xff; b1[0x04] = FZ >> 16 & 0xff; b1[0x05] = FZ >> 24;
b1[0x06] = 0; b1[0x07] = 0; b1[0x08] = 0; b1[0x09] = 0;
b1[0x0a] = 0x36; b1[0x0b] = 0; b1[0x0c] = 0; b1[0x0d] = 0;
b1[0x0e] = 0x28; b1[0x0f] = 0; b1[0x10] = 0; b1[0x11] = 0;
b1[0x12] = WT & 0xff; b1[0x13] = WT >> 8 & 0xff; b1[0x14] = WT >> 16 & 0xff; b1[0x15] = WT >> 24;
b1[0x16] = HT & 0xff; b1[0x17] = HT >> 8 & 0xff; b1[0x18] = HT >> 16 & 0xff; b1[0x19] = HT >> 24;
b1[0x1a] = 0x1; b1[0x1b] = 0; b1[0x1c] = 0x18; b1[0x1d] = 0;
b1[0x1e] = 0; b1[0x1f] = 0; b1[0x20] = 0; b1[0x21] = 0;
b1[0x22] = BZ & 0xff; b1[0x23] = BZ >> 8 & 0xff; b1[0x24] = BZ >> 16 & 0xff; b1[0x25] = BZ >> 24;
b1[0x26] = 0; b1[0x27] = 0; b1[0x28] = 0; b1[0x29] = 0;
b1[0x2a] = 0; b1[0x2b] = 0; b1[0x2c] = 0; b1[0x2d] = 0;
b1[0x2e] = 0; b1[0x2f] = 0; b1[0x30] = 0; b1[0x31] = 0;
b1[0x32] = 0; b1[0x33] = 0; b1[0x34] = 0; b1[0x35] = 0;
// initialize
init1();
// making bitmap data
draw1();
// output file
err = fopen_s(&ftp, "sn.bmp", "wb");
if (err != NULL) return err;
for (ui = 0; ui < 0x36; ui++) {
fputc(b1[ui], ftp);
}
for (ui = 0; ui < BZ; ui++) {
fputc(b2[ui], ftp);
}
err = fclose(ftp);
if (err != NULL) return err;
err = fopen_s(&ftp, "cn.bmp", "wb");
if (err != NULL) return err;
for (ui = 0; ui < 0x36; ui++) {
fputc(b1[ui], ftp);
}
for (ui = 0; ui < BZ; ui++) {
fputc(b3[ui], ftp);
}
err = fclose(ftp);
if (err != NULL) return err;
err = fopen_s(&ftp, "dn.bmp", "wb");
if (err != NULL) return err;
for (ui = 0; ui < 0x36; ui++) {
fputc(b1[ui], ftp);
}
for (ui = 0; ui < BZ; ui++) {
fputc(b4[ui], ftp);
}
err = fclose(ftp);
if (err != NULL) return err;
err = fopen_s(&ftp, "el.txt", "w");
if (err != NULL) return err;
fprintf(ftp, "Jacobi elliptic function constants\n");
fprintf(ftp, "k = %10.5g, k^2 = %10.5g, k' = %10.5g, k'^2 = %10.5g\n", elk, elk * elk, elkc, elkc * elkc);
fprintf(ftp, "1/k = %10.5g, k'/k = %10.5g\n", 1 / elk, elkc / elk);
fprintf(ftp, "K = %10.5g, K' = %10.5g, K/K' = %10.5g\n", ellk, ellkc, ellk / ellkc);
fprintf(ftp, "K/(pi/2) = %10.5g, K'/(pi/2) = %10.5g\n", ellk / pi4 / 2.0, ellkc / pi4 / 2.0);
fprintf(ftp, "q = %10.5g, te2(0) = %10.5g, te3(0) = %10.5g, te0(0) = %10.5g\n", elq, te2a, te3a, te0a);
fprintf(ftp, "q' = %10.5g, tf2(0) = %10.5g, tf3(0) = %10.5g, tf0(0) = %10.5g\n", elqc, tf2a, tf3a, tf0a);
fprintf(ftp, "horizontal: WT = %6i, CT = %10.5g, D = %10.5g\n", WT, UC, UD);
fprintf(ftp, "vertical: HT = %6i, CT = %10.5g, D = %10.5g\n", WT, VC, VD);
fprintf(ftp, "northern hemisphere parallels: (degree) value\n");
for (z = 0; z < pi4 - 0.001; z += DD) {
fprintf(ftp, "(%5.2f) %10.5g\n", z / pi4 * 90.0, tan(pi4 + z) * alf);
}
fprintf(ftp, "north polar (infinity) area = %10.5g(deg)\n", atan(anp) / pi4 * 90.0);
fprintf(ftp, "southern hemisphere parallels: (degree) value\n");
for (z = 0; z < pi4 - 0.001; z += DD) {
fprintf(ftp, "(%5.2f) %10.5g\n", z / pi4 * 90.0, tan(pi4 - z) * alf);
}
fprintf(ftp, "south polar (zero point) area = %10.5g(deg)\n", atan(asp) / pi4 *90.0);
err = fclose(ftp);
if (err != NULL) return err;
printf("complete\n");
return err;
}
上記のプログラムと本ブログに掲載の関連図の著作権は私にあります。しかし、改造などはご自由になさってください。明らかな改造後のプログラムの著作権はあなたのものとなります。係数などを必要に応じて変更した、プロクラムが出力するグラフもあなたのものです。私に連絡する必要はありませんし、許諾なども必要ありません。