教育は公平に見せかけて格差を作る道具！？

以前も似たような記事を書いたが再びｗ。

息子のネット塾へ参加している中学生は、タイの最高峰マヒドン高校対策をするバンコクの理科の塾へ通っているそうで、そこでは電気回路の「Superposition」を教えていると息子へ知らせてくれたそうだ。
「Superpositionって何？」と私へ尋ねるが私も知らず、息子へ「ググレカス」と思いながらもネットで検索。日本では「重ね合わせの理」と言われる物だが、物理で『波』の重ね合わせを学んだ記憶は有っても、『電気回路』で重ね合わせを学んだ記憶は無し。底辺校なのでやらなかったか、それとも忘れてしまったのか？

ホワイトボードで息子へ説明し、「知識が有れば簡単に解ける問題も知らなければ手出しが出来ない。いつもやってる数学のギフテッド問題と同じだな」と息子と話していると、「あ！、それ私は知ってるよ！」と言う娘。どこで習ったか尋ねると、少６で通った理科の塾で教えたそうだ。

私も知らないし、息子も知らないので普通の高校では教えないと思うが、それが小学生や中学生相手の塾で教えられて、入試へ出題されたり。
教育は公平に見せかけて格差を作る道具だと子供達へ話し、格差をつける側とつけられる側のどちらが良いかと話した。

我が家はずっと格差をつけられる側だが、せめて一矢報いてやろうと親子で勉強中ｗ。さて前回の記事で紹介した数学の問題の解答。

問１



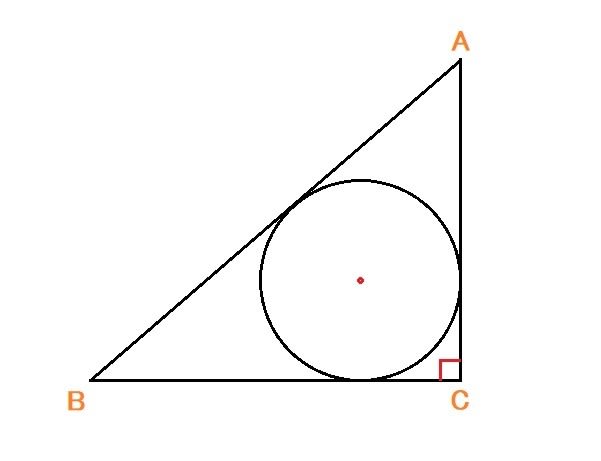
斜辺ＡＢの長さが５ｃｍで、内接円の半径が１ｃｍの直角三角形ＡＢＣの面積を求めなさい。

先ずはJIMMYさんから頂いた解答。



円と辺ABの間の接点ＰとしてＰＡ＝x、PB＝5-ｘとしますと、この三角形の面積は1/2（2×（5-ｘ））+1/2（2ｘ）+1になるのでこれを解くと6です。
答え　６ｃ㎡

三角形ＡＢＣの面積は、底辺（５－ｘ）×高さ（ｒ＝１）÷２の三角形が２個と底辺（ｘ）×高さ（ｒ＝１）÷２の三角形が２個と１×１の正方形の和。
（１／２）×（５－ｘ）×１×２＋（１／２）×ｘ×１×２＋１＝（５－ｘ）＋ｘ＋１＝６


次はtaiyaiさんから頂いた解答。（私の都合で改変しました。m(_ _)m）



円の中心０からＡＢ、ＡＣ、ＢＣにそれぞれ垂線を下す。この時、円との接点をＤ、Ｅ、Ｆとする。
ＡＤ＝ｘ、ＢＤ＝ｙとする。ＡＦ＝ｘ、ＢＥ＝ｙになる。ＯＤ＝ＯＦ＝１。
小さい三角形４個と 正方形の面積＝１ との和を求める。
三角形ＡＤＯとＡＦＯの面積はともに２分のｘ、２つ足せばｘになる。
三角形ＯＤＢとＯＥＢの面積の和はｙとなる。

これより三角形ＡＢＣの面積Ｓ＝ｘ＋ｙ＋１。
ｘ＋ｙ＝５なので、　　　　Ｓ＝５＋１＝６
答え　６ｃ㎡

そして私の解答。



ＢＥ＝ＢＤ＝ｂ－ｒ＝ｂ－１　　（ｒは内接円の半径）
ＡＦ＝ＡＤ＝ｃ－ｒ＝ｃ－１
ＡＢ＝ＢＤ＋ＡＤ＝（ｂ－１）＋（ｃ－１）＝ｂ＋ｃ－２＝５
ｂ＋ｃ＝７　---①
⊿ＡＢＣ＝⊿ＯＡＢ＋⊿ＯＢＣ＋⊿ＯＣＡ
　　　　＝（１／２）・５・１＋（１／２）・ｂ・１＋（１／２）・ｃ・１
　　　　＝（１／２）（５＋ｂ＋ｃ）
①より
⊿ＡＢＣ＝（１／２）（５＋７）
　　　　＝６
答え　６ｃ㎡

次は番外編で、こういう解き方も出来るかなと思ったのだが・・・



⊿ＡＢＣ＝底辺（５）×高さ（１＋√２）÷２
　　　　≒５×２．４１４÷２＝６．０３５　　　あれ他と違う答えｗ。

上の図ではＤＣは直線に見えるが・・



この様に書いてみるとＤＣは必ず直線とは限らないのが判る。
ＤＣが直線になるのは⊿ＡＢＣがＢＣ＝ＡＣの直角二等辺三角形の時であり、問ではＢＣとＡＣの長さは決められてないので、ＢＣ＝ＡＣとして解いてみる。



∠Ｃが９０°の直角三角形ＡＢＣは、ＢＣ＝ＡＣの時に∠Ａ＝∠Ｂ＝４５°の直角二等辺三角形となり、ＡＢ：ＢＣ：ＡＣ＝√２：１：１（覚える）なので、ＡＢ：ＢＣ＝√２：１＝５：ＢＣより　１×５（内側同士を掛ける）＝√２×ＢＣ（外側同士を掛ける）　でＢＣ＝５／√２と判る。
ＢＣ＝ＡＣ＝５／√２。
この直角二等辺三角形の内接円の半径ｒは⊿ＡＢＣの面積＝（ｒ／２）（ＡＢ＋ＢＣ＋ＡＣ）で求められる（←の式の意味が分からない方は上の私の解答を参照）ので、
⊿ＡＢＣの面積（１／２）×（５／√２）×（５／√２）＝（ｒ／２）（５＋（５／√２）＋（５／√２））
２５／４＝（ｒ／２）（５＋１０／√２）
２５／２＝ｒ（５＋１０／√２）
　　　ｒ＝（２５／２）／（５＋１０／√２）
　　　　＝２５／（２×（５＋１０／√２））
　　　　＝２５／（２×（５＋１０√２／２）
　　　　≒２５／（２×（５＋７.０７））
　　　　＝２５／２４.１４
　　　　≒１.０４

斜辺が５ｃｍの⊿ＡＢＣが直角二等辺三角形の時、内接円の半径ｒ≒１.０４ｃｍ。
問の内接円の半径は１ｃｍなので、直角三角形ＡＢＣは直角二等辺三角形ではなく、ＤＣはこの時直線ではない。
よって⊿ＡＢＣ＝底辺（５）×高さ（１＋√２）÷２と計算できないのが判る。

長くなったので、今日はここまでで終わりたい。
問２の解答は次回！


タイの中学生向け数学ギフテッド問題の記事へのリンク→#高１入試ギフ



貴方のクリックとコメントが、このブログのパワーの源です。
下の２つのバナーへ応援クリックをお願いします。

海外生活ブログ タイ情報 人気ランキングはこちら
リアルタイムに更新される新着記事一覧（右下）からタイの今が見える。お薦め。

タイの人気ブログが大集合！！
登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。