メネラウスの定理の式を使わずに問２を解く

前回の記事ではメネラウスの定理の式を使って問２を簡単に解いたのだが、

問題集の模範解答であるメネラウスの定理の式を使わない方法も紹介しておきたい。

問２



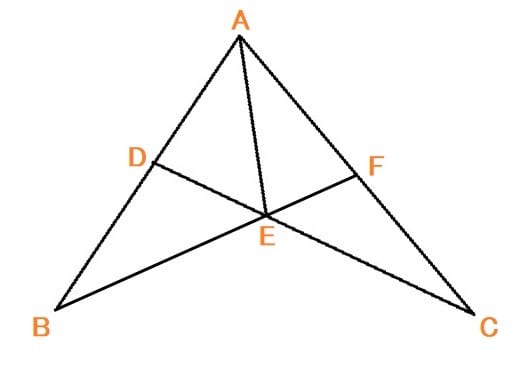
ＡＦ＝ＦＣ＝ＡＥ＝ＤＢ、ＥＦ＝２ｃｍ、ＤＡ＝４ｃｍの時のＡＣの長さを求めなさい。

先ずは解答を判り易くする為に図を左に倒し、補助線ＢＣを引く。

⊿ＡＥＦの面積をｙとすると、⊿ＡＥＦと高さも底辺の長さも等しい⊿ＣＥＦの面積もｙ。
よって⊿ＡＣＥの面積は２ｙとなる。



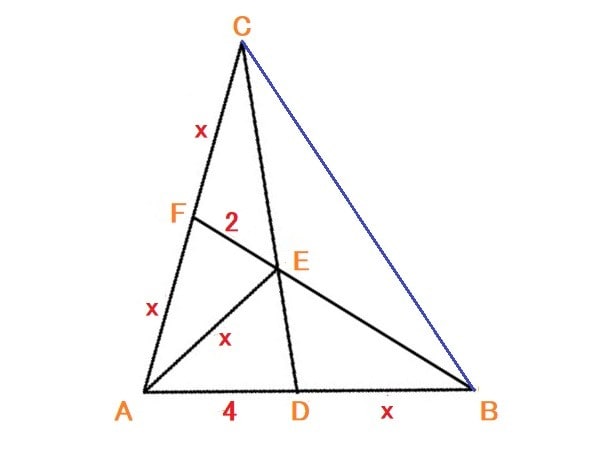
⊿ＡＣＤと⊿ＢＣＤは高さが同じ三角形で、この２つの三角形の面積比はそれぞれの三角形の底辺の長さに比例するので、
⊿ＡＣＤ：⊿ＢＣＤ＝ＡＤ：ＤＢ＝４：ｘ
⊿ＡＣＤ・ｘ＝⊿ＢＣＤ・４
⊿ＢＣＤ＝（⊿ＡＣＤ・ｘ）／４　---①

⊿ＡＥＤと⊿ＢＥＤは高さが同じ三角形で、この２つの三角形の面積比はそれぞれの三角形の底辺の長さに比例するので、
⊿ＡＥＤ：⊿ＢＥＤ＝ＡＤ：ＤＢ＝４：ｘ
⊿ＡＥＤ・ｘ＝⊿ＢＥＤ・４
⊿ＢＥＤ＝（⊿ＡＥＤ・ｘ）／４　---②

①－②
⊿ＢＣＤ－⊿ＢＥＤ＝（（⊿ＡＣＤ・ｘ）／４）－（（⊿ＡＥＤ・ｘ）／４）
⊿ＢＣＥ＝（ｘ／４）（⊿ＡＣＤ－⊿ＡＥＤ）
　　　　＝（ｘ／４）⊿ＡＣＥ
　　　　＝（ｘ／４）２ｙ＝（ｘ・ｙ）／２

⊿ＣＥＦと⊿ＢＣＥは高さが同じ三角形で、この２つの三角形の面積比はそれぞれの三角形の底辺の長さに比例するので、
⊿ＣＥＦ：⊿ＢＣＥ＝ｙ：（ｘ・ｙ）／２＝２：ＥＢ
ｙ・ＥＢ＝（（ｘ・ｙ）／２）・２
ＥＢ＝（ｘ・ｙ）／ｙ＝ｘ

メネラウスの定理を使わず、高さが同じ三角形の面積比は底辺の長さの比と等しいのを利用してＥＢの長さはｘと分かった。

ＡＣの長さの求め方は前回の記事の解答と同じ。



ＡからＥＦへ垂線を下ろし、ＥＦとの交点をＨ、ＡＨの長さをｈとする。
直角三角形ＡＦＨの辺の長さをピタゴラスの定理で表すと
ＡＦ²＝ＡＨ²＋ＨＦ²
ｘ²＝ｈ²＋１²
ｈ²＝ｘ²－１　---①
直角三角形ＡＢＨの辺の長さをピタゴラスの定理で表すと
ＡＢ²＝ＡＨ²＋ＢＨ²
（ｘ＋４）²＝ｈ²＋（ｘ＋１）²
①より　ｈ²＝ｘ²－１　なので、
（ｘ＋４）²＝ｘ²－１＋（ｘ＋１）²
ｘ²＋８ｘ＋１６＝ｘ²－１＋ｘ²＋２ｘ＋１
ｘ²－６ｘ－１６＝０
（ｘ－８）（ｘ＋２）＝０
ｘ＝－２，８
ｘ＞０なのでｘ＝８
ＡＣの長さは２ｘなので　２×８＝１６
答え　ＡＣ＝１６ｃｍ

「高さが同じ複数の三角形の面積比はそれぞれの三角形の底辺の長さに比例する」のは知ってても、類似の問題へ取り組んで何度も経験しておかないと試験で使えないと実感。ブログの記事として残しておこうと思った。

タイの中学生向け数学ギフテッド問題の記事へのリンク→#高１入試ギフ

タイの高校生向け数学入試問題の記事へのリンク→#大学入試


貴方のクリックとコメントが、このブログのパワーの源です。
下の２つのバナーへ応援クリックをお願いします。

海外生活ブログ タイ情報 人気ランキングはこちら
リアルタイムに更新される新着記事一覧（右下）からタイの今が見える。お薦め。

タイの人気ブログが大集合！！
登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。