勉強が苦手で、数学なんて大嫌いな私が問題を解いてみる「タイの中学の数学に悩む」シリーズ第三弾!
今回は割った余りを求める問題。
引用元は

の左の赤い方(1分冊)で、代数と三角関数の問題集。紹介している問題は代数の問題から。
問題106

A=(1!)2000+2(2!)2000+3(3!)2000+・・・+2000(2000!)2000
A÷7の余りを求めなさい。

数字の後ろへ付いている!は階乗であり、数学において非負整数 n の階乗(かいじょう、英: factorial)n ! は、1 から n までのすべての整数の積である。例えば、6!=6×5×4×3×2×1=720である。空積の規約のもと 0! = 1 と定義する。 Wikipedia 階乗より引用。
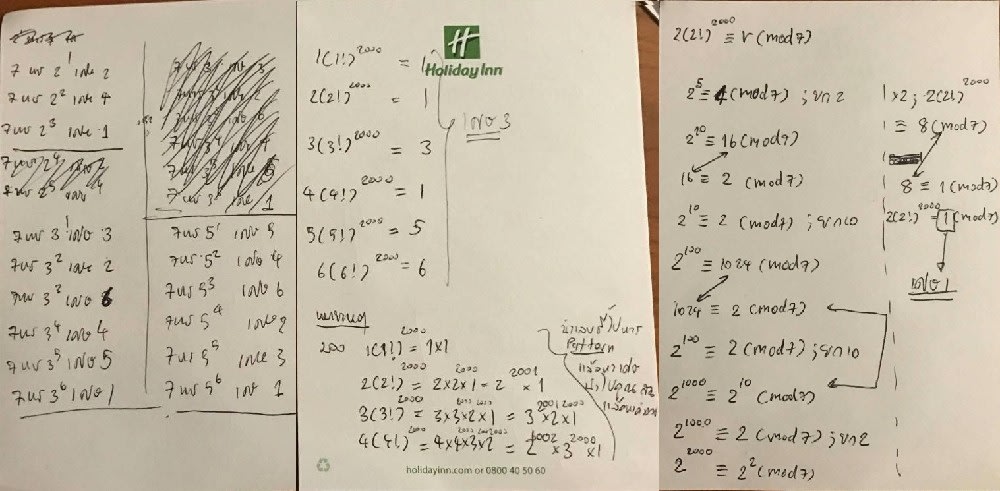
7!より上は、必ず7を掛けているので余りは無いのに気が付いたので、(1!)2000+2(2!)2000+3(3!)2000+・・・+6(6!)2000を7で割った余りを求めれば良いということ。
解答を読んでも(2!)2000を7で割った余りの求め方を紹介しているだけで、答えを求める仕組みの説明は無し。
賢い皆様は分かるのだろうが、私にはさっぱり。息子へ尋ねても同様で\(TヘT)/お手上げ状態。
息子が高校受験を手伝った後輩がタイの名門校のスワンクラープへ通っており、その子は国の物理オリンピック要員で数学も得意と言うのでLINEで問い合わせ。実家はウドンのお金持ちで、夏休みなので英国旅行中だったそうだがちょっとお手伝いをお願い。説明を書いて送ってくれて電話で息子へ説明してくれたが、送り手の性能が良くても、受け手の性能が悪いので話が噛み合わずでサッパリ。こっちは朝でも向こうは夜中。寝ないで頑張らせるのも悪いので、お礼を言って電話を切らせた。
こうなったらお馬鹿な私でも頑張るしか無い。頼めるのはGoogle先生とWikipedia先生。
検索して見つけたのが、こちらのtsujimotterのノートブックで「3の100乗を19で割ったあまりは?」を4通りの方法で計算するの記事。
方法1:地道に計算する(難易度:★☆☆☆☆)
方法2:周期性を使う(難易度:★★☆☆☆)
方法3:フェルマーの小定理を使う(難易度:★★★☆☆)
方法4:平方剰余の相互法則を使う(難易度:★★★★★)
と4つの方法が紹介されており、方法1はいくらなんでも無理と手を出せず、方法2はこちらのページを知る前にチラッと気が付いて取り組んだが全体像が見えなくて途中で挫折。ということで「方法3:フェルマーの小定理を使う」にチャレンジ。
詳細はリンク先を読んで欲しいが、要するにnを7で割る時はn7-1=6毎に余りが1になるということ。
これを 26≡1(mod7)と表し、26を7で割った余りは1の意味になる。≡の左右は=と同様に掛けたりべき乗計算したり出来る。これを使った計算が分り易く説明されているのが下の動画。
What is the reminder for 3 power 100 divided by 7
1!2000は1なので、1÷7=0余り1
2(2!)2000
=2(2×1)2000
=2・22000・12000
=22001
2001÷6=333余り3なので
22001
=(26)333・23
フェルマーの小定理より
26≡1(mod7)であり、
(26)333・23≡1333・23(mod7)
(26)333・23≡8(mod7)
8は7で割れるので8÷7=1余り1
(26)333・23≡1(mod7)
2(2!)2000≡1(mod7)
2(2!)を7で割った余りは1
同様に
3(3!)2000
=3(3×2×1)2000
=32001・22000・12000
=32001・22000
2001÷6=333余り3なので
32001
=(36)333・33
フェルマーの小定理より
36≡1(mod7)であり、
(36)333・33≡1333・33(mod7)
(36)333・33≡27(mod7)
27は7で割れるので27÷7=3余り6
(36)333・33≡6(mod7)
32001≡6(mod7)
32001を7で割った余りは6
2000÷6=333余り2なので
22000
=(26)333・22
フェルマーの小定理より
26≡1(mod7)であり、
(26)333・22≡1333・22(mod7)
(26)333・22≡4(mod7)
22000≡4(mod7)
22000を7で割った余りは4
32001・22000≡6・4(mod7)
32001・22000≡24(mod7)
24は7で割れるので 24÷7=3余り3
32001・22000≡3(mod7)
3(3!)2000≡3(mod7)
次は・・
4(4!)2000
=4(4×3×2×1)2000
=4(24)2000
2000÷6=333余り2なので
242000
=(246)333・242
フェルマーの小定理より
246≡1(mod7)であり、
(246)333・242≡1333・242(mod7)
(246)333・242≡576(mod7)
576は7で割れるので576÷7=82余り2
242000≡2(mod7)
4(24)2000≡4・2(mod7)
4(24)2000≡8(mod7)
8は7で割れるので、8÷7=1余り1
4(24)2000≡1(mod7)
4(4!)2000≡1(mod7)
同様にやって5(5!)2000の余りが5、6(6!)2000の余りが6。(疲れたwww)
A÷7の余りは 1!2000から6(6!)2000の余りを足して
1+1+3+1+5+6=17 17÷7=2余り3。
A÷7の余りは3。
お疲れ様~♪
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
貴方のクリックとコメントが、このブログのパワーの源です。
下の2つのバナーへ応援クリックをお願いします。
 海外生活ブログ タイ情報 人気ランキングはこちら
海外生活ブログ タイ情報 人気ランキングはこちら
リアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。
 タイの人気ブログが大集合!!
タイの人気ブログが大集合!!
登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。

今回は割った余りを求める問題。
引用元は

の左の赤い方(1分冊)で、代数と三角関数の問題集。紹介している問題は代数の問題から。
問題106

A=(1!)2000+2(2!)2000+3(3!)2000+・・・+2000(2000!)2000
A÷7の余りを求めなさい。

数字の後ろへ付いている!は階乗であり、数学において非負整数 n の階乗(かいじょう、英: factorial)n ! は、1 から n までのすべての整数の積である。例えば、6!=6×5×4×3×2×1=720である。空積の規約のもと 0! = 1 と定義する。 Wikipedia 階乗より引用。
7!より上は、必ず7を掛けているので余りは無いのに気が付いたので、(1!)2000+2(2!)2000+3(3!)2000+・・・+6(6!)2000を7で割った余りを求めれば良いということ。
解答を読んでも(2!)2000を7で割った余りの求め方を紹介しているだけで、答えを求める仕組みの説明は無し。
賢い皆様は分かるのだろうが、私にはさっぱり。息子へ尋ねても同様で\(TヘT)/お手上げ状態。
息子が高校受験を手伝った後輩がタイの名門校のスワンクラープへ通っており、その子は国の物理オリンピック要員で数学も得意と言うのでLINEで問い合わせ。実家はウドンのお金持ちで、夏休みなので英国旅行中だったそうだがちょっとお手伝いをお願い。説明を書いて送ってくれて電話で息子へ説明してくれたが、送り手の性能が良くても、受け手の性能が悪いので話が噛み合わずでサッパリ。こっちは朝でも向こうは夜中。寝ないで頑張らせるのも悪いので、お礼を言って電話を切らせた。

こうなったらお馬鹿な私でも頑張るしか無い。頼めるのはGoogle先生とWikipedia先生。
検索して見つけたのが、こちらのtsujimotterのノートブックで「3の100乗を19で割ったあまりは?」を4通りの方法で計算するの記事。
方法1:地道に計算する(難易度:★☆☆☆☆)
方法2:周期性を使う(難易度:★★☆☆☆)
方法3:フェルマーの小定理を使う(難易度:★★★☆☆)
方法4:平方剰余の相互法則を使う(難易度:★★★★★)
と4つの方法が紹介されており、方法1はいくらなんでも無理と手を出せず、方法2はこちらのページを知る前にチラッと気が付いて取り組んだが全体像が見えなくて途中で挫折。ということで「方法3:フェルマーの小定理を使う」にチャレンジ。
詳細はリンク先を読んで欲しいが、要するにnを7で割る時はn7-1=6毎に余りが1になるということ。
これを 26≡1(mod7)と表し、26を7で割った余りは1の意味になる。≡の左右は=と同様に掛けたりべき乗計算したり出来る。これを使った計算が分り易く説明されているのが下の動画。
What is the reminder for 3 power 100 divided by 7
1!2000は1なので、1÷7=0余り1
2(2!)2000
=2(2×1)2000
=2・22000・12000
=22001
2001÷6=333余り3なので
22001
=(26)333・23
フェルマーの小定理より
26≡1(mod7)であり、
(26)333・23≡1333・23(mod7)
(26)333・23≡8(mod7)
8は7で割れるので8÷7=1余り1
(26)333・23≡1(mod7)
2(2!)2000≡1(mod7)
2(2!)を7で割った余りは1
同様に
3(3!)2000
=3(3×2×1)2000
=32001・22000・12000
=32001・22000
2001÷6=333余り3なので
32001
=(36)333・33
フェルマーの小定理より
36≡1(mod7)であり、
(36)333・33≡1333・33(mod7)
(36)333・33≡27(mod7)
27は7で割れるので27÷7=3余り6
(36)333・33≡6(mod7)
32001≡6(mod7)
32001を7で割った余りは6
2000÷6=333余り2なので
22000
=(26)333・22
フェルマーの小定理より
26≡1(mod7)であり、
(26)333・22≡1333・22(mod7)
(26)333・22≡4(mod7)
22000≡4(mod7)
22000を7で割った余りは4
32001・22000≡6・4(mod7)
32001・22000≡24(mod7)
24は7で割れるので 24÷7=3余り3
32001・22000≡3(mod7)
3(3!)2000≡3(mod7)
次は・・
4(4!)2000
=4(4×3×2×1)2000
=4(24)2000
2000÷6=333余り2なので
242000
=(246)333・242
フェルマーの小定理より
246≡1(mod7)であり、
(246)333・242≡1333・242(mod7)
(246)333・242≡576(mod7)
576は7で割れるので576÷7=82余り2
242000≡2(mod7)
4(24)2000≡4・2(mod7)
4(24)2000≡8(mod7)
8は7で割れるので、8÷7=1余り1
4(24)2000≡1(mod7)
4(4!)2000≡1(mod7)
同様にやって5(5!)2000の余りが5、6(6!)2000の余りが6。(疲れたwww)
A÷7の余りは 1!2000から6(6!)2000の余りを足して
1+1+3+1+5+6=17 17÷7=2余り3。
A÷7の余りは3。
お疲れ様~♪
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
貴方のクリックとコメントが、このブログのパワーの源です。
下の2つのバナーへ応援クリックをお願いします。
 海外生活ブログ タイ情報 人気ランキングはこちら
海外生活ブログ タイ情報 人気ランキングはこちらリアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。
 タイの人気ブログが大集合!!
タイの人気ブログが大集合!!登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。











難しいですねえ。
タイの学生 数学オリンピックで金銀銅独占ですね。
メンカームさんも大変ですね。脳みそ使いすぎて
焼き付きそうですね。大学入試レベルですね。タイの大学生で解けるひとは おそらく 100人いないのでは。 文科系ならたぶん誰もいないでしょう。まあ10人らいはおるかな。
まあ 2000の階乗、2000乗というのがはったりですね。この弱い人は見ただけで卒倒しそう。7で割ったあまりだけ出せというのが味噌ですね。合計を出せと言われたら
一生かかっても答えは出せない。
また暇なときにでもやってみよう。
えらいですね。降参します。あほらしくなってきた。
可愛い娘の為とは言え、
数学どころか勉強が大嫌いな私がやるには難しすぎでした。
最初はいろいろ頑張って見まして、余りに周期性がありそうなのには気が付きましたが、
周期の規則性を解明できず、フェルマーさんほど根気がないので、ネットのお世話になりました。
ネットの解説が無ければ永遠に解けなかったでしょう。
解説付きでも汗をかきました。
やるとそれが頭から離れません。そこで今日ゆっくり読みました。
フェルマーの小定理も読みました。これの証明はかなり難しいです。2項定理 とか順列組み合わせとか
必要です。かなり賢い高校生レベルです。これは何とか思い出してええ加減に理解できました。証明は合同数と関係ありませんでした。
しかし合同数は私の時代は高校でやっていません。50年前ですから。だから思い出すのではなく 今から学習することになります。これには時間がかかります。だから最初は降参したのです。ほかに勉強することがいまたくさんあるからです。数学は塾の先生でもすれば将来役に立ちますが、70歳75歳の先生のところにきてくれたらよいですが。飯の種に成ればよいのですが、ということ前回はいまさらあほらしいと書いたのです。塾の先生も面白いですけど 賢い子は大手の塾に行く時代です。しかしやる気のない子を教える気はありません。もう人生の無駄です。残り少ない人生です。
しかし今日やはり 無視できない心が生じました。
この問題では
フエルマーの小定理を憶えているのが大事ですね。
要するにmod 7
の時は ある数字の6乗は必ず1になるという事ですね。これを使ってよいとのことで解きました。7の階乗以下の数列は常に0なので関係ないとのことですね。そうですね。メンカームさんも 今や、塾の先生ができそうですね。
最初見た時はそれすらわかりませんでした。まさにはったり問題ですね。
だから数字の1998乗は必ず1ですね。
6乗をさらに333乗したものですね。
3から計算します。
3(3!)2000乗の計算
(3!)=6 6の2000乗は
6の1998乗 かける 6の2乗。
6の1998乗は6の6乗 のさらに333乗。
である数字の1998乗というのは常に1.
答えは 3x36≡3x36 、、36≡1
なので 答えは3x1≡3
4(4!)2000乗。 の計算は
4の階乗は24 、、、(24の1998乗)は1
そこで 答えは4x(24の2乗。)
24≡ 3、 4x(24の2乗。)≡ 4x9≡36
36≡1
5(5!)2000乗。の計算
5(5!)2000乗。の計算
5!=120≡1 5ⅹ1x120x120≡5
6(6!)2000乗の計算は
6!=720≡6、6の1998乗は1、、 36≡1
答え 6x1x720x720≡6x6x6≡6x36
≡6x1
メンカームさんの答えと同じになりました。よかった。
お疲れ様でした。
合同数は私も学んだ記憶がありません。
今回が初めてだったと思います。
便利なやり方があるのだなと関心しました。
数学塾の先生・・ウドンでは年配の方がやられる塾が話題になってます。
お子さんが全てマヒドン付属高校へ行かれたそうで、
姪御さんへも教えられ、その子は娘と同じ学年で数学は県で三番手。
かなりイイお値段を言われるそうで、知人から一緒に行かせないかと誘われましたが
馬鹿は馬鹿なりに私が教えようと断りました。
大手の塾は情報を多く持ってますが、きめ細かさが足りませんし、
授業時間も学校と比べると遥かに少ないですから問題数も少なめ。
だからウドンでトップの子は1教科に複数の塾と家庭教師だそうです。
メインの学習は大手塾へ任せて、サポート役が良いかも知れませんね。
やる気のない子供は、周囲がどんなに頑張っても無駄でしょう。
私は学校の勉強に全く興味がありませんでしたから、自分でもわかりますw。
娘とやるギフテッドの数学は解けないと悔しいですし、
解答を読んでも理解できないと、もっと腹が立つ。
会社員の時は仕事の問題を寝ながら夢の中で考えて解決した事もありましたが、
最近は数学の夢を見るようになりました。
教科書は貰ったらすぐに読んでしまい、
授業中は全然面白くないので寝てたのですが、
子供の頃に勉強しておけば良かったと五十を過ぎた今頃に後悔(恥w)。
ブログの記事にした様な見ただけで心が折れそうな問題の解き方でも
学校で教えてくれたなら、面白がって勉強したかも?
息子はもう手遅れなんですが、娘だけでも勉強を面白がってくれるならと期待して
子供のサポートを続けたいと思ってます。
いつも御協力ありがとうございます。
教科書は貰ったらすぐに読んでしまい、
授業中は全然面白くないので寝てたのですが、>>
まだまだ頭は柔らかいですね。脳細胞が退化していませんね。もしもっと学校での成績に執着していたら 、メンカームさんは帝大レベルに入学できていたと思います。
しかし頭を使うことは娘さんのためになるし、いつまでも呆けないでいられるので健康にもプラスですね。夢を失ったときに老いるというのも真実ですし。
ところで合同数の話ですが
例えば24の2乗のあまりと
先に 24を3に合同してから
2乗する数字 の余り、が なぜ同じになるのかというのは 勘と少しの経験で 少しインチキしました。
しかし。これは定理として必ずある
はずです。
mod7で
やってみました。
すべての数字は7m+aで書けるはずです。 これの2乗は7m7m+7ma +aa≡aa,,
今度は3乗します。
(7m+a)(7m+a)(7m+a)=
(7m7m+7ma +aa))(7m+a)=(7m7m+7ma +aa)7m+
(7m7m+7ma +aa)a ≡ aaa
となります。これを何回やっても
結局7mのついてないのは 一番最後のa乗数のみ、 の項だけになります。(7m+a)のn乗は、(aのn乗)と合同である。
という事で ある数字のn乗は
先に、ある数字を一番小さい合同数に変換してから これをn乗した
数字と合同であると大体証明されました。(7m+a)のn乗は、(aのn乗)と合同である。
大事な点は 7で割り切った余りの数字でないといけませんね。
中途半端の合同数ではいけません。
一番小さな合同数に変換するという事ですね。
この場合だけしか証明されていませんので。
これで自信をもって使えます。
ところでお分かりとおもいますが
2x3x4x5の計算では
3x4x(2x5)で暗算で120です。当たり前ですよね。まあ親切心からという事で。
がんばってください。自分の脳力の為にもなりますよ。まだまだ若い。若僧ですよ。555.
私も 若僧に戻りたいです。
mugaさんの秀才の甥御さんとか ほかの親切な読者の方もおられるので良かったですね。