
「中田敦彦のYouTube大学」の「フェルマーの最終定理」が超絶面白かったので、原作である本書も読んでみた。他の関連動画も少し見たので、この問題に関する歴史やエピソードはある程度頭に入った状態で読むことになった。なので、本書で初めてこの物語を知った読者が味わったであろう胸熱展開の感動は、あまりなかった。
まあいいんだけど。
文学作品とかと違って、前提情報がないとレビューを読むかたも困ると思うので、少し説明します。
17世紀フランスの裁判官、ピエール・ド・フェルマーは数学が趣味で、難しい問題を考えては数学者に送り付け、解けなくて苦しむ様子を見て喜んでいた。そのフェルマーが、ディオファントスの『算術』という本のピタゴラスの定理(下記)を、ちょっと改造したのが事の発端。
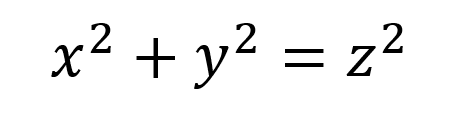
中学校でやったやつ。「直角三角形の斜辺の2乗は、他の辺の2乗の和に等しい」である。いろんな図形を三角形に分け、「1、1、√2」と「1、√3、2」を使って長さを出したりした。この物語においては自然数x、y、zについての定理なので、美しいやつで言えば「3、4、5」の組み合わせがある。
で、フェルマーは、これ、3乗にすると組み合わせが見つからないぞ? いや、3乗以上は全部ないわ、と気づいた。
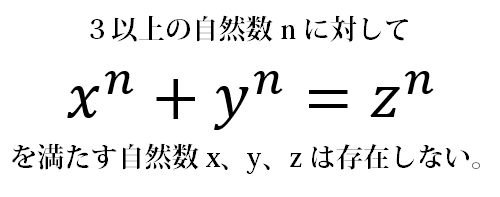
そして「私は真に驚くべき方法でこれを証明したが、それを書くには余白が狭すぎる」と本に書きこんだ。
フェルマーの死後、大量に書き込みのある『算術』を息子が発見。これは売れると思ったのか、父親の書き込み入りバージョンを出版した。未知の定理が多数出て来たことで数学界は大騒ぎになる。フェルマーの書き込みは1つ1つ証明されていき、最後に残ったのが上の奴だった。
数学の世界では、ほとんど正しいけど証明されてはいないものを「予想」というらしい。フェルマーのこれも、厳密には予想だが、本人が証明したと書き残しているので「定理」と呼ばれる。だがフェルマーはプロの数学者ではなくアマチュアなので、きちんと証明を書いていない。その素人がやった証明に、世界中の数学者たちが挑み続けた360年の歴史を綴ったのが本書である。
隻眼の天才、レオンハルト・オイラーは、フェルマーがすでにn=4の場合を証明しているのを見つけ、その無限降下法と虚数を用いてn=3の場合を証明した。
フランスが生んだ最も知性的な女性、ソフィー・ジェルマンは、nが素数、2n+1も素数で、x、y、zのどれもnで割り切れない場合を証明した。彼女の理論を利用してn=5とn=7の場合が証明できた。ここまで約150年かかっている。n=4ができると4の倍数は全部できるそうだが、素数はまだ無限に残っている。この辺を描いた本書第3章のタイトルは「数学の恥」という。
欧米の有名数学者たちが、奮闘むなしく敗れ去り、でも次のチャレンジャーにバトンを渡す。だが証明は遅々として進まない。という流れできて戦後、物語の舞台はなんと日本に移る。ここが日本人には熱い。本書が日本でもベストセラーになった理由の一つは、ここにあると思う。
谷山豊と志村五郎が、楕円方程式(楕円曲線)とモジュラー形式は同じだとする「谷山=志村予想」を発表する。楕円方程式のE系列とモジュラーのM系列はそれぞれ無限にあるのだが、それぞれ互いに対応するのがあるはず、という感じ…だと思う。
で、ゲルハルト・フライが「谷山=志村予想が正しければフェルマーの最終定理も正しい」と言い出す。フェルマーの最終定理に解があると仮定すると、あの式は楕円方程式の形に変形できるのだが、その式は異常なのでモジュラーではない。全ての楕円曲線はモジュラーだとする谷山=志村予想に反する。つまり、フェルマーの最終定理が間違っていれば(解があれば)、谷山=志村予想も間違っている(モジュラーではない楕円曲線が存在する)ことになる。これを逆にいうと、谷山=志村予想が正しければフェルマーの最終定理も正しい、ということになるのだ。
そして「フェルマーの最終定理」を解くことになるアンドリュー・ワイルズ登場。と言いたいところだが、本書はワイルズのインタビューを挟みながら数学の歴史をたどる構成になっているため、真打登場の感はない。
ワイルズが「フェルマーの最終定理」に挑む際の面白エピソードは、当然中田敦彦の動画より詳しく描かれている。ニック・カッツにコリヴァギン・フラッハ法の使い方をチェックしてもらうための偽装講座は「楕円曲線の計算」という、どうとでも取れるタイトルにしたとか。
ワイルズが基本的に一人でこっそり取り組んでいた理由が、なるほどなあと思った。途中経過でも漏れると、それを利用して誰かが研究を進めてしまうかもしれない。やってることが漏れると、誰かが競りかけてくるかもしれない。実際、宮岡洋一が先にフェルマーの最終定理を証明したと発表し、ワイルズが超焦るシーンがある。だが、宮岡の証明は失敗に終わり、日本人的にはちょっと悲しい話でもあった。ていうか、そんな日本人がいたのね。
最終決戦となるケンブリッジ大学での講義は、フェルマーの最終定理の証明(谷山=志村予想の証明)だということを伏せて行われた。カール・ルービンが仲間に送った電子メールで、初日、二日目と、じわじわ期待が膨らんでいく様子を表現するのが上手い。どうもフェルマーの最終定理らしいと察知された三日目、歴史的瞬間を見届けようと集結する数学者たちが熱い。そして「ここで終わりにしたいと思います」と証明を〆るワイルズ。大歓声。拍手喝采。動画がないかと検索してみたが、さすがに残ってないようだ。
ここで終わってれば美しかったのだが、そうではないんだよな。証明に穴があったことが判明する。その穴を指摘した第3部担当レフェリーが、カッツだったというのが皮肉というか美しくなかった。カッツがチェックしたはずのコリヴァギン・フラッハ法の部分に論理のギャップがあり、それをカッツ自身が見つけてしまったという。
悪戦苦闘の末、その穴は岩澤健吉の「岩澤理論」を使うことでふさがり、「フェルマーの最終定理」は無事に、正式に証明された。また日本人が関与。スティーブ・ジョブズみたいなのが日本から出てこないとよく言われるが、凄い人出てるじゃん。もっと報道されてもいいと思うけど。
うーん。流れの紹介みたいになってしまったので、本書そのもののレビューも。
「フェルマーの最終定理」がいかに難問か、どれだけの数学者がさじを投げてきたか、ということが、各章各エピソードの冒頭で紹介される。とんでもないラスボスだってことはわかってるので、ちょっとしつこいと思った。他にも、数学とは、数学者とは、みたいな話が、何度も同じように繰り返されるのが、本書の最大の欠点かな。著者がテレビのプロデューサーなので、ドラマが前回までのあらすじを毎回入れるように、そういうのを入れたんだろう。そういうのを刈り込めば、もっとコンパクトになったと思う。
各種動画を見てて「ワイルズの証明はフェルマーがやったと言ってる証明と同じか」と疑問に思っていたのだが、本書では、最新の理論であるコリヴァギン・フラッハ法などは使われてないはずなので、多分違うと書かれている。そうだとしたら、そしてフェルマーが本当に証明したのなら、古典的な、多分もう少しシンプルなやり方で証明しているわけで、それを探すという課題もあるんだろう。それも何百年もかかりそうだ。
僕は文系人間で、この文章でもナントカ定理だのナントカ法だの偉そうに書いているが、内容はさっぱりわかっていない。が、そんな僕でも本書を読んで、1つの問題について、何か閃くまでいろんな方向からじっくり考えるのは楽しいことかも、と思った。すぐその気になってしまうタチなので。
最初の方で、胸熱展開の感動はあまりなかったと書いたが、こうして振り返ると、結構あったかも。















