先ずはお知らせから。
11月30日(金)から12月9日(日)までセントラルプラザウドンタニの4階ホールでウドンタニ ブックフェスティバルが開催される。

毎年娘が楽しみにしており、今年も連れて行く予定。娘はキャラクター商品、私は子供向けの英語の古本狙い。
さて、本文。
25日の日曜はサマーコム・カニッタサー試験。私が住むウドンタニから一番近い会場はコンケンで、前泊して受験に備える生徒も居るが、我が家は早朝5時起きで6時に出発してコンケンへ向かった。
娘は車へ枕と掛け布団を持ち込んで後部座席で熟睡していたので、制限速度より少し控えめの安全運転。7時過ぎにコンケン手前のガソリンスタンドへ入って朝食。ちょうど8時頃に試験会場へ到着。
妻と娘を降ろして、私は公園の駐車場で日陰を確保し、YOUTUBEで動画を見ながらウトウトw。娘はすぐに試験会場の教室へ向かったそうで、妻は顔見知りのご父兄を見つけて受験談義が定番。
今年は一緒に座ったのがUP校の1年生で成績トップな生徒のご両親。そして妻の隣に来て座られたのが、UP校3年生のトップグループの一人のお父さん。このお父さんは既に子供二人をタイの最高峰マヒドン高校へ入れられており、今年は3人目をチャレンジ中。そして進学塾を経営されており、ウドンタニでマヒドン高校を狙える塾の最右翼とも言われている。
この大変濃いご父兄達の間に座った妻は耳を大きく広げ、一言も聞き漏らさない様に情報収集。数学の試験だったので、話題は数学の学習法が中心だったそうだが、皆さんが悩んでおられたのが、パラボラ(放物線)の学習。タイの中学生向けの数学問題集を見ると判るが、タイの中学生は簡単なパラボラしか学校で習わず、塾や参考書でも深く詳しく解説するのは少ない。娘へ学ばせようと買った日本の中学数学の参考書を見た息子が、こんな難しいパラボラの問題は大学受験にも出ないと言ったくらいだ。
しかしながらマヒドン高校の受験には出るそうで、マヒドン対策を謳った問題集にもあるが、そういう問題を上手く教える先生がウドンタニでは見つからないので、どうするかって話が中心だったそうだ。
日本の問題をやる試験(数検?)へ行かせたが、さっぱりだったと塾もやられるお父さんが仰ったそうで、自分の子供はバンコクの塾へ行かしておられるが、それでも足りないので、お金を出し合ってパラボラが得意な先生をウドンタニへ呼ぶ話まで出たそうだ。
昨年も有名高校の入試対策に何人かが集まってバンコクの先生を呼んで教えて貰った話が耳に入っており、しっかりアンテナを上げておかないと気が付かないかも?そうやって差が広がるので、気を付けたいと思った。
もう一つお知らせ。
受験談義の話題にもなった「数検」だが、来年1月6日にタイでも試験があり、12月25日まで申し込みを受付中。タイ国内で10ヶ所以上の会場が有り、イサーンでもコンケン・ウボン・ナコンパノムで受験可能。
タイの数検のページは上の画像からリンクしているので、クリック↑。
それでは、先週末に出題した数学の問題の解答をやろう。
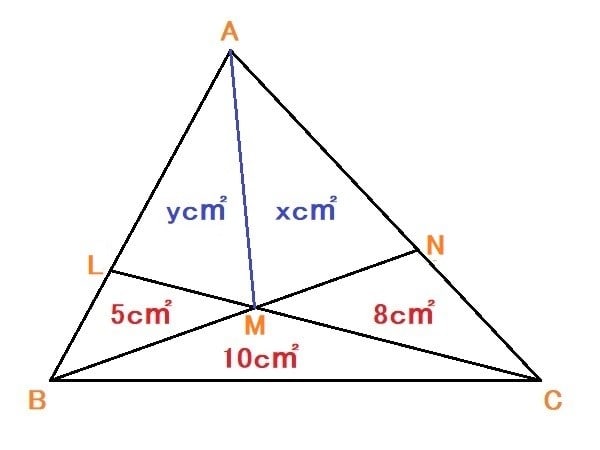
問 四角形LMNAの面積を求めなさい。
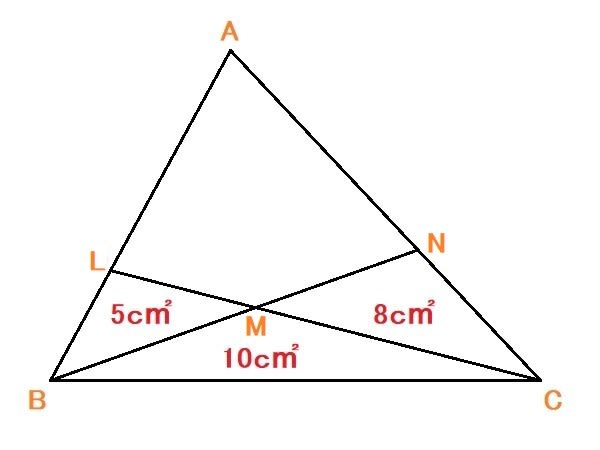
先ずは問題集の模範解答。

タイ語が読めない(数学も苦手w)ので、先週末に出題した時点でさっぱり意味が分からなかったのだが、1つ1つ数式を追ってようやく理解した。

⊿BMC=10c㎡(タイ語の原文はタランヌアイ=平方ヌアイ(単位)。ややこしいので以下c㎡で行く)
辺MCの真ん中を点Oとし、 BOへ線を引く。
⊿BMO=⊿BOC=5c㎡
⊿BLM=5c㎡なので
LM=MO=OC
⊿MNC=8c㎡
MO=OCであり、ONへ線を引く。
⊿MNO=⊿ONC=4c㎡
⊿MLN=4
何度も書くが私はタイ語が読めないので、上は数式から想像して書いてある。
この部分をメンカーム式に書くと・・・

⊿BLMと⊿BMCは高さが等しい三角形で、2つの三角形の面積比は底辺の長さの比に等しいので、
⊿BLM:⊿BMC=5:10=LM:MC=2:1
⊿MLNと⊿NMCも高さが等しい三角形で、2つの三角形の面積比は底辺の長さの比に等しいので、
LM:MC=2:1=⊿MLN:⊿NMC=4:8
⊿MLN=4c㎡
⊿LAN=xc㎡ とすると
⊿LAN/⊿LNC=x/(4+8)=x/12=AN/NC ---①
⊿ABL/⊿NBC=(5+4+x)/(10+8)=(9+x)/18=AN/NC ---②
①=②なので
x/12=(9+x)/18
18x=12(9+x)
18x=108+12x
6x=108
x=18
⊿LAN=18c㎡
∴ 四角形LMNA=⊿LAN+⊿MLN=18+4=22c㎡
JIMMYさんから頂いた解答
以前、うちの数学の教授は数学を解くには、すぐアキラめることだと言ってましたね。
要するに解こう解こうと迷路に入り込んでしまうからダメで、諦めて入口に戻ったほうが早いという事でしょう。
AMの間に線を引いて、三角形AMNの面積をx、三角形ALMの面積をyとします。四角形LMNAの面積は(x+y)です。
この三角形ABCをまず左に回します。
三角形ALCの面積は(8+x+y)、三角形BLCの面積は(5+10)です。
三角形の面積は底辺×高さ÷2ですが、三角形ALCと三角形BLCは高さが同じで底辺だけが違います。(8+x+y):(5+10)=AL:BLです。
次に小さい方の三角形ALMの面積y:三角形BLMの面積5も高さが同じなのでy:5=AL:BL。つまり(8+x+y):(5+10)=y:5です。
次に三角形ABCをまず右に回します。
三角形ANBの面積は(5+x+y)、三角形CNBの面積は(8+10)です。
(5+x+y):(8+10)=AN:NC
三角形AMNの面積は(x)、三角形NMCの面積は(8)です。
x:8=AN:NC=(5+x+y):(8+10)
これで連立方程式
5×(8+x+y)=15y と
8×(5+x+y)=18x が出来ます。
これを解くとx=12、y=10、ですので
これを解くと、四角形LMNAの面積は(x+y)=22㎤です。
メンカームのコメント。
先ずは、いつも解答を下さるJIMMYさんへ感謝!
「数学を解くには、すぐアキラめることだ」
娘が解くのを黙って見ていると、1問を解くのに時には1時間も掛けて頑張ったり。
それでも解ければ良いが、多くの場合は深みに嵌って解けない・・・w。
最近はキッチンタイマーを使って5分で制限しようとするが、嫌がっている様子。
解法の引き出しがまだ少ないので、解けなければ解答を見せるしかないのが現状w。
娘がもう少し経験を積めば、深みに嵌まるのに気が付くだろうと期待するが・・。
最後に私、メンカームの解答

点Aと点Mを直線で結び、⊿ALM=x ⊿AMN=y とする。
高さが等しい2つの三角形の面積比は底辺の長さの比に等しいので、
⊿MNA:⊿MCN=AN:NC
y:8=AN:NC
⊿BMA:⊿BCM=AN:NC
(5+x):10=AN:NC
y:8=(5+x):10=AN:NC
10y=8(5+x) A:B=C:Dの時、AD=BC
10y=40+8x ---①
同様に・・
⊿MAL:⊿MLB=AL:LB
x:5=AL:LB
⊿CAM:⊿CMB=AL:LB
(y+8):10=AL:LB
x:5=(y+8):10=AL:LB
10x=5(y+8)
10x=5y+40
5y=10x-40
10y=20x-80 ---②
①=②
40+8x=20x-80
12x=120
x=10
①より
10y=40+8・10
10y=120
y=12
四角形LMNA=x+y=10+12=22
答え 22c㎡
それでは今週の1問w

AE/EC=BD/DA=1/2
CD//EF
□EFDG/⊿ABC を求めなさい。
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
タイの高校生向け数学入試問題の記事へのリンク→#大学入試
貴方のクリックとコメントが、このブログのパワーの源です。
下の2つのバナーへ応援クリックをお願いします。
 海外生活ブログ タイ情報 人気ランキングはこちら
海外生活ブログ タイ情報 人気ランキングはこちら
リアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。
 タイの人気ブログが大集合!!
タイの人気ブログが大集合!!
登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。

11月30日(金)から12月9日(日)までセントラルプラザウドンタニの4階ホールでウドンタニ ブックフェスティバルが開催される。

毎年娘が楽しみにしており、今年も連れて行く予定。娘はキャラクター商品、私は子供向けの英語の古本狙い。
さて、本文。
25日の日曜はサマーコム・カニッタサー試験。私が住むウドンタニから一番近い会場はコンケンで、前泊して受験に備える生徒も居るが、我が家は早朝5時起きで6時に出発してコンケンへ向かった。
娘は車へ枕と掛け布団を持ち込んで後部座席で熟睡していたので、制限速度より少し控えめの安全運転。7時過ぎにコンケン手前のガソリンスタンドへ入って朝食。ちょうど8時頃に試験会場へ到着。
妻と娘を降ろして、私は公園の駐車場で日陰を確保し、YOUTUBEで動画を見ながらウトウトw。娘はすぐに試験会場の教室へ向かったそうで、妻は顔見知りのご父兄を見つけて受験談義が定番。
今年は一緒に座ったのがUP校の1年生で成績トップな生徒のご両親。そして妻の隣に来て座られたのが、UP校3年生のトップグループの一人のお父さん。このお父さんは既に子供二人をタイの最高峰マヒドン高校へ入れられており、今年は3人目をチャレンジ中。そして進学塾を経営されており、ウドンタニでマヒドン高校を狙える塾の最右翼とも言われている。
この大変濃いご父兄達の間に座った妻は耳を大きく広げ、一言も聞き漏らさない様に情報収集。数学の試験だったので、話題は数学の学習法が中心だったそうだが、皆さんが悩んでおられたのが、パラボラ(放物線)の学習。タイの中学生向けの数学問題集を見ると判るが、タイの中学生は簡単なパラボラしか学校で習わず、塾や参考書でも深く詳しく解説するのは少ない。娘へ学ばせようと買った日本の中学数学の参考書を見た息子が、こんな難しいパラボラの問題は大学受験にも出ないと言ったくらいだ。
しかしながらマヒドン高校の受験には出るそうで、マヒドン対策を謳った問題集にもあるが、そういう問題を上手く教える先生がウドンタニでは見つからないので、どうするかって話が中心だったそうだ。
日本の問題をやる試験(数検?)へ行かせたが、さっぱりだったと塾もやられるお父さんが仰ったそうで、自分の子供はバンコクの塾へ行かしておられるが、それでも足りないので、お金を出し合ってパラボラが得意な先生をウドンタニへ呼ぶ話まで出たそうだ。
昨年も有名高校の入試対策に何人かが集まってバンコクの先生を呼んで教えて貰った話が耳に入っており、しっかりアンテナを上げておかないと気が付かないかも?そうやって差が広がるので、気を付けたいと思った。
もう一つお知らせ。
受験談義の話題にもなった「数検」だが、来年1月6日にタイでも試験があり、12月25日まで申し込みを受付中。タイ国内で10ヶ所以上の会場が有り、イサーンでもコンケン・ウボン・ナコンパノムで受験可能。

タイの数検のページは上の画像からリンクしているので、クリック↑。
それでは、先週末に出題した数学の問題の解答をやろう。
問 四角形LMNAの面積を求めなさい。

先ずは問題集の模範解答。

タイ語が読めない(数学も苦手w)ので、先週末に出題した時点でさっぱり意味が分からなかったのだが、1つ1つ数式を追ってようやく理解した。

⊿BMC=10c㎡(タイ語の原文はタランヌアイ=平方ヌアイ(単位)。ややこしいので以下c㎡で行く)
辺MCの真ん中を点Oとし、 BOへ線を引く。
⊿BMO=⊿BOC=5c㎡
⊿BLM=5c㎡なので
LM=MO=OC
⊿MNC=8c㎡
MO=OCであり、ONへ線を引く。
⊿MNO=⊿ONC=4c㎡
⊿MLN=4
何度も書くが私はタイ語が読めないので、上は数式から想像して書いてある。
この部分をメンカーム式に書くと・・・

⊿BLMと⊿BMCは高さが等しい三角形で、2つの三角形の面積比は底辺の長さの比に等しいので、
⊿BLM:⊿BMC=5:10=LM:MC=2:1
⊿MLNと⊿NMCも高さが等しい三角形で、2つの三角形の面積比は底辺の長さの比に等しいので、
LM:MC=2:1=⊿MLN:⊿NMC=4:8
⊿MLN=4c㎡
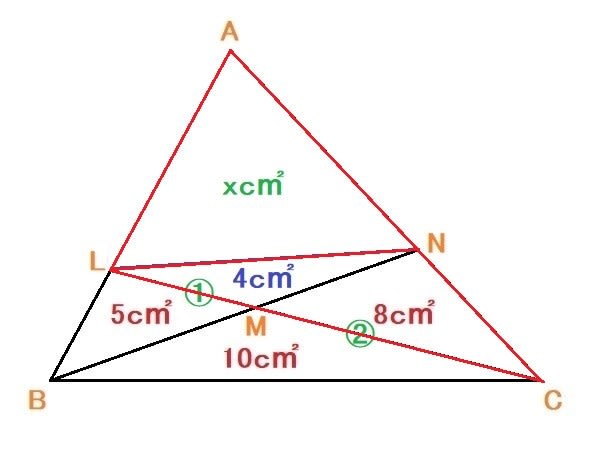
⊿LAN=xc㎡ とすると

⊿LAN/⊿LNC=x/(4+8)=x/12=AN/NC ---①

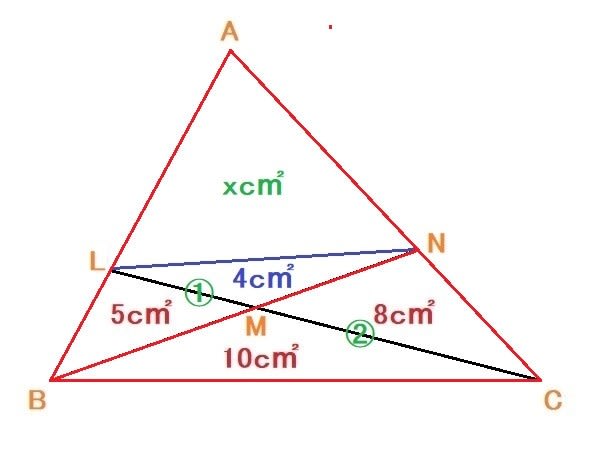
⊿ABL/⊿NBC=(5+4+x)/(10+8)=(9+x)/18=AN/NC ---②
①=②なので
x/12=(9+x)/18
18x=12(9+x)
18x=108+12x
6x=108
x=18
⊿LAN=18c㎡
∴ 四角形LMNA=⊿LAN+⊿MLN=18+4=22c㎡
JIMMYさんから頂いた解答
以前、うちの数学の教授は数学を解くには、すぐアキラめることだと言ってましたね。
要するに解こう解こうと迷路に入り込んでしまうからダメで、諦めて入口に戻ったほうが早いという事でしょう。
AMの間に線を引いて、三角形AMNの面積をx、三角形ALMの面積をyとします。四角形LMNAの面積は(x+y)です。

この三角形ABCをまず左に回します。
三角形ALCの面積は(8+x+y)、三角形BLCの面積は(5+10)です。
三角形の面積は底辺×高さ÷2ですが、三角形ALCと三角形BLCは高さが同じで底辺だけが違います。(8+x+y):(5+10)=AL:BLです。
次に小さい方の三角形ALMの面積y:三角形BLMの面積5も高さが同じなのでy:5=AL:BL。つまり(8+x+y):(5+10)=y:5です。
次に三角形ABCをまず右に回します。
三角形ANBの面積は(5+x+y)、三角形CNBの面積は(8+10)です。
(5+x+y):(8+10)=AN:NC
三角形AMNの面積は(x)、三角形NMCの面積は(8)です。
x:8=AN:NC=(5+x+y):(8+10)
これで連立方程式
5×(8+x+y)=15y と
8×(5+x+y)=18x が出来ます。
これを解くとx=12、y=10、ですので
これを解くと、四角形LMNAの面積は(x+y)=22㎤です。
メンカームのコメント。
先ずは、いつも解答を下さるJIMMYさんへ感謝!
「数学を解くには、すぐアキラめることだ」
娘が解くのを黙って見ていると、1問を解くのに時には1時間も掛けて頑張ったり。
それでも解ければ良いが、多くの場合は深みに嵌って解けない・・・w。
最近はキッチンタイマーを使って5分で制限しようとするが、嫌がっている様子。
解法の引き出しがまだ少ないので、解けなければ解答を見せるしかないのが現状w。
娘がもう少し経験を積めば、深みに嵌まるのに気が付くだろうと期待するが・・。
最後に私、メンカームの解答

点Aと点Mを直線で結び、⊿ALM=x ⊿AMN=y とする。
高さが等しい2つの三角形の面積比は底辺の長さの比に等しいので、
⊿MNA:⊿MCN=AN:NC
y:8=AN:NC
⊿BMA:⊿BCM=AN:NC
(5+x):10=AN:NC
y:8=(5+x):10=AN:NC
10y=8(5+x) A:B=C:Dの時、AD=BC
10y=40+8x ---①
同様に・・
⊿MAL:⊿MLB=AL:LB
x:5=AL:LB
⊿CAM:⊿CMB=AL:LB
(y+8):10=AL:LB
x:5=(y+8):10=AL:LB
10x=5(y+8)
10x=5y+40
5y=10x-40
10y=20x-80 ---②
①=②
40+8x=20x-80
12x=120
x=10
①より
10y=40+8・10
10y=120
y=12
四角形LMNA=x+y=10+12=22
答え 22c㎡
それでは今週の1問w

AE/EC=BD/DA=1/2
CD//EF
□EFDG/⊿ABC を求めなさい。
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
タイの高校生向け数学入試問題の記事へのリンク→#大学入試
貴方のクリックとコメントが、このブログのパワーの源です。
下の2つのバナーへ応援クリックをお願いします。
 海外生活ブログ タイ情報 人気ランキングはこちら
海外生活ブログ タイ情報 人気ランキングはこちらリアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。
 タイの人気ブログが大集合!!
タイの人気ブログが大集合!!登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。


















