先週末は某私立大医学部の入試を息子が受験。電話で「どうだった」と尋ねると、「女の子は綺麗だし・・・」なんて言い出す息子。
「てめぇ何しに大学へ行ったんだ!」ヽ(`Д´)ノプンプン と言うと真面目な話を始めたが、英語と数学は高校の定期試験レベルでも、生物と化学は『糞』難しかったそうだ。
息子の話では、その大学医学部専門に対策する塾があるそうで、やはりそういうところで勉強しないと難しいかも。
持ち出し厳禁な入試問題を試験の立ち会いをされる先生がスマホで撮影していたそうで、そうやって塾では入試対策をするのだろう。
火曜には合格発表があったが、当然息子の名前は無しw。私が見ていても、とてもそんなレベルではない。
さて、先週末の記事で出題した数学の問題の解答をしよう。
問 ∠Aの角度を求めなさい。
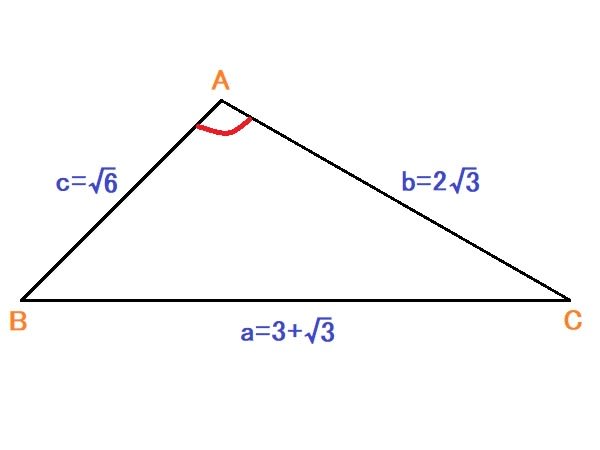
問題集の模範解答
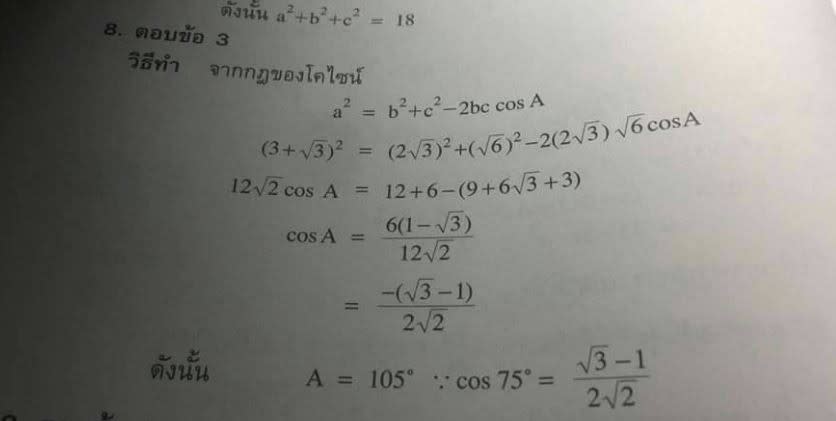
2つの辺の長さと 1つの内角の大きさが分かっていれば、もう 1 つの辺の長さが決まるという第二余弦定理を利用してcosA=-(√3-1)/(2√2)を求め A=105°と答えているのだが、関数電卓も三角関数表も使わずに cosA=-(√3-1)/(2√2) から A=105°をどうやって求めるかと言うのが息子から私への質問だった。
三角定規の角度である30°・45°・60°の三角関数の値を知っているのは教科書レベルで中学生以上なら常識だが、それ以外はどうするか?教科書レベルでも苦しい私に分かる訳も無く、別の方法で解いたのだが、taiyaiさんが三角関数の加法定理を教えて下さったので紹介しよう。
三角関数の加法定理 sin
sin(A+B)=sinA・cosB+cosA・sinB
sin(A-B)=sinA・cosB-cosA・sinB
sin15°=sin(45°-30°)=sin45°・cos30°-cos45°・sin30°
=(1/√2)(√3/2)-(1/√2)(1/2)=(√3/2√2)-(1/2√2)
=(√3-1)/(2√2)=(√6-√2)/4
sin75°=sin(30°+45°)=sin30°・cos45°+cos30°・sin45°
=(1/2)(1/√2)+(√3/2)(1/√2)=(1/2√2)+(√3/2√2)
=(√3+1)/(2√2)=(√6+√2)/4
sin105°=sin(60°+45°)=sin60°・cos45°+cos60°・sin45°
=(√3/2)(1/√2)+(1/2)(1/√2)=(√3/2√2)+(1/2√2)=sin75°
sin105°=sin75°に気が付いて調べると補角公式というそうだ。(全く覚えてないが、高さは一緒だからだなw)
sin105°=sin(180°-75°)=sin75°
sin120°=sin(180°-60°)=sin60°
sin135°=sin(180°-45°)=sin45°
sin150°=sin(180°-30°)=sin30°
三角関数の加法定理 cos
cos(A+B)=cosA・cosB-sinA・sinB
cos(A-B)=cosA・cosB+sinA・sinB
cos15°=cos(45°-30°)=cos45°・cos30°+sin45°・sin30°
=(1/√2)(√3/2)+(1/√2)(1/2)=(√3/2√2)+(1/2√2)
=(√3+1)/(2√2)=(√6+√2)/4
cos75°=cos(45°+30°)=cos45°・cos30°-sin45°・sin30°
=(1/√2)(√3/2)-(1/√2)(1/2)=(√3/2√2)-(1/2√2)
=(√3-1)/(2√2)=(√6-√2)/4
これも補角公式があるそうで・・
cos105°=cos(180°-75°)=-cos75°
cos120°=cos(180°-60°)=-cos60°
cos135°=cos(180°-45°)=-cos45°
cos150°=cos(180°-30°)=-cos30°
マイナスが付くのは底辺が逆向きだからかな?w
補角公式や加法定理は「ウィキペディアの三角関数」のページ、大学受験対策の三角関数については「高校数学の基本問題の三角関数の加法定理,倍角公式,3倍角公式,半角公式」のページを参考にして欲しい。
息子の数学のレベルが低い話を妻としていると、高校数学の塾へ通っている娘曰く『「15°と75°の2つだから三角関数の値は暗記しろ」って塾の先生が言ってたよ」だそうだ。それと補角公式で足りるってことだ。
息子へ電話して「おめぇは今まで何を勉強してんだ!全然足りねぇじゃねぇか!!!」と叱る私。親が足りないから子が足りなのだが、悔しいったらありゃしない。(大恥w)
私、メンカームの別解答
上の方法で解けなくてやった別の解法。cosAの値に見覚えが無いのでcosBの値から角度を調べようとした。
b2=a2+c2-2ac・cosB
(2√3)2=(3+√3)2+(√6)2-2(3+√3)・√6・cosB
2(3+√3)・√6・cosB=(3+√3)2+(√6)2-(2√3)2
2√6(3+√3)・cosB=9+3+6√3+6-12
cosB=(6√3+6)/(2√6(3+√3))=(6(1+√3))/(2・√6・√3(1+√3))
=6/(2・√2・√3・√3)=1/√2
点Aから辺BCの垂線を引き、辺BCとの交点をDとする。
BD=AB・cosB=√6×(1/√2)=√3
DC=BC-BD=3+√3-√3=3
cosB=1/√2 より ∠B=45°
AD=AB・sinB=AB・sin45°=√6×(1/√2)=√3
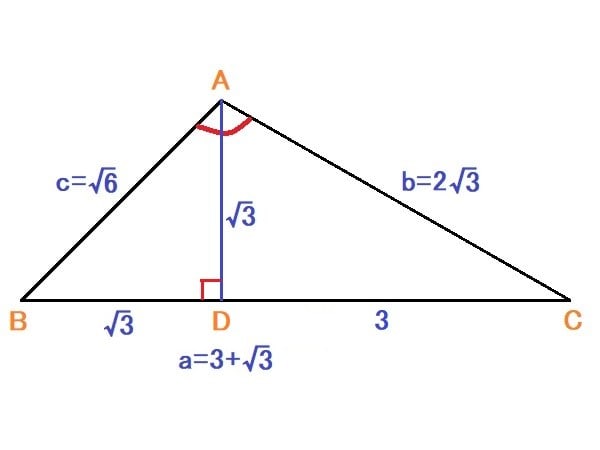
cos∠BAD=AD/AB=√3/√6=1/√2
∠BAD=45°
cos∠CAD=AD/AC=√3/(2√3)=1/2
∠CAD=60°
∠A=∠BAD+∠CAD=45°+60°=105°
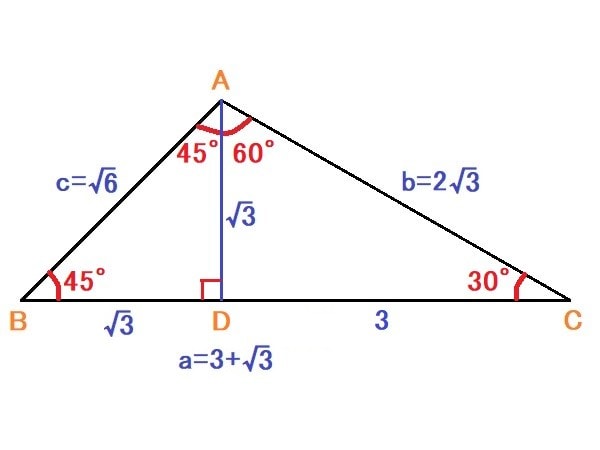
答え ∠A=105°
JIMMYさんから頂いた解答
大学入試という事なので、じっくり解法ではなく、高速解法でやってみます。所要時間1分。
AからBCに垂線を下ろし交点をDとします。三平方の定理で
三角形ABDはBD^2+AD^2=AB^2=6、三角形ADCはCD^2+AD^2=AC^2=12
※BCは3+√3ですが、BD=√3、DC=3のようですね。
そうなるとAD=√3だから
三角形ABDは直角二等辺三角形なので∠BAD=45°
三角形ADCは正三角形を半分にした形なので∠CAD=60°
∠BAC=45+60=105°です。
※は瞬間的に閃くと解くのが速くなります。

メンカームのコメント
先ずはいつも協力して下さるJIMMYさんへ感謝!m(_ _)m
ピタゴラスの定理を利用して解いてあり、この方法なら中学生でも解ける。
私がもう少し細かく解説しよう。
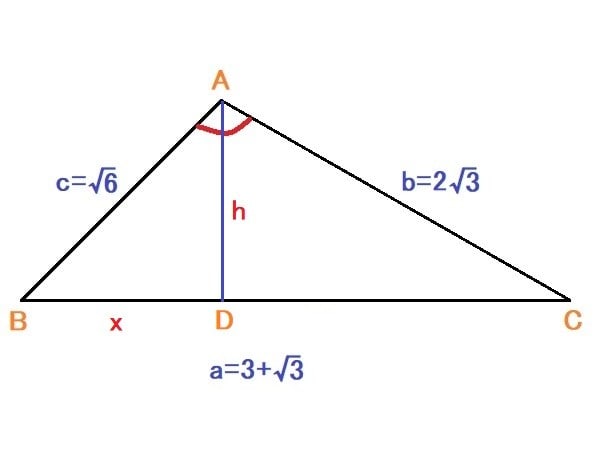
BD=x、AD=h とする。
三角形ABDについてピタゴラスの定理の式を作ると
AB2=BD2+AD2
(√6)2=x2+h2 ---①
三角形ACDについてピタゴラスの定理の式を作ると
AC2=CD2+AD2
(2√3)2=(3+√3-x)2+h2
12 = 9+3+x2+6√3-2√3x-6x+h2
x2+h2+6√3-2√3x-6x=0
①よりx2+h2=(√6)2なので
(√6)2+6√3-2√3x-6x=0
(6+2√3)x=6+6√3
x=(6+6√3)/(6+2√3)=(6(1+√3))/(2√3(1+√3))=3/√3=√3
①より
(√6)2=x2+h2
6=3+h2
h2=3
h=√3
DC=BC-BD=3+√3-√3=3

三角形ABDの辺の長さの比は AD:BD:AB=√3:√3:√6=1:1:√2 なので、
三角形ABDは、直角二等辺三角形の三角定規(45°45°90°の角をもつ)と相似。
よって∠BAD=45°
三角形ACDの辺の長さの比は AD:AC:CD=√3:2√3:3=1:2:√3 なので、
三角形ACDは、正三角形を半分にした直角三角形の三角定規(30°60°90°の角をもつ)と相似。
よって∠CAD=60°

∠A=∠BAD+∠CAD=45°+60°=105°
答え ∠A=105°
大学入試対策問題集からの設問だが、中学生が知っているピタゴラスの定理で解けた。\(^o^)/
もう数学はエエよと否定的な声が聞こえそうだが、中学生向けのサマーコムカニッタサー問題集より今週の1問。(シリーズ化か?w)
問題集の模範解答を見ても意味が分からなかった問題。私は別の方法で解いた。
問 四角形LMNAの面積を求めなさい。(誤記修正しました。m(_ _)m)
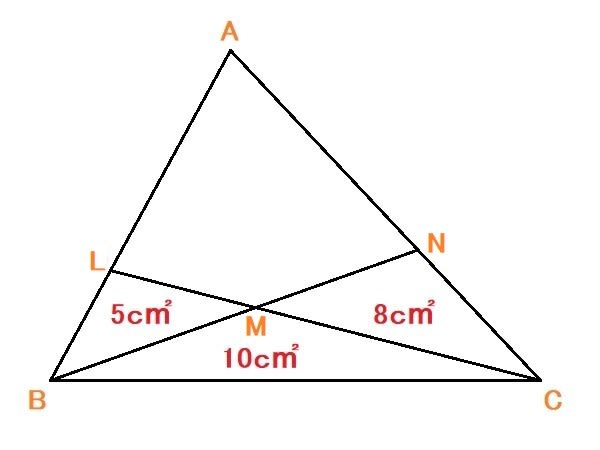
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
タイの高校生向け数学入試問題の記事へのリンク→#大学入試
貴方のクリックとコメントが、このブログのパワーの源です。
下の2つのバナーへ応援クリックをお願いします。
 海外生活ブログ タイ情報 人気ランキングはこちら
海外生活ブログ タイ情報 人気ランキングはこちら
リアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。
 タイの人気ブログが大集合!!
タイの人気ブログが大集合!!
登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。

「てめぇ何しに大学へ行ったんだ!」ヽ(`Д´)ノプンプン と言うと真面目な話を始めたが、英語と数学は高校の定期試験レベルでも、生物と化学は『糞』難しかったそうだ。
息子の話では、その大学医学部専門に対策する塾があるそうで、やはりそういうところで勉強しないと難しいかも。
持ち出し厳禁な入試問題を試験の立ち会いをされる先生がスマホで撮影していたそうで、そうやって塾では入試対策をするのだろう。
火曜には合格発表があったが、当然息子の名前は無しw。私が見ていても、とてもそんなレベルではない。
さて、先週末の記事で出題した数学の問題の解答をしよう。
問 ∠Aの角度を求めなさい。

問題集の模範解答
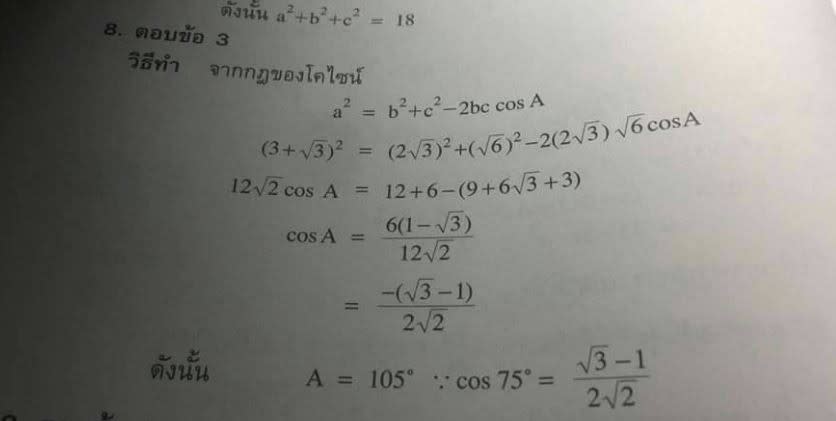
2つの辺の長さと 1つの内角の大きさが分かっていれば、もう 1 つの辺の長さが決まるという第二余弦定理を利用してcosA=-(√3-1)/(2√2)を求め A=105°と答えているのだが、関数電卓も三角関数表も使わずに cosA=-(√3-1)/(2√2) から A=105°をどうやって求めるかと言うのが息子から私への質問だった。
三角定規の角度である30°・45°・60°の三角関数の値を知っているのは教科書レベルで中学生以上なら常識だが、それ以外はどうするか?教科書レベルでも苦しい私に分かる訳も無く、別の方法で解いたのだが、taiyaiさんが三角関数の加法定理を教えて下さったので紹介しよう。
三角関数の加法定理 sin
sin(A+B)=sinA・cosB+cosA・sinB
sin(A-B)=sinA・cosB-cosA・sinB
sin15°=sin(45°-30°)=sin45°・cos30°-cos45°・sin30°
=(1/√2)(√3/2)-(1/√2)(1/2)=(√3/2√2)-(1/2√2)
=(√3-1)/(2√2)=(√6-√2)/4
sin75°=sin(30°+45°)=sin30°・cos45°+cos30°・sin45°
=(1/2)(1/√2)+(√3/2)(1/√2)=(1/2√2)+(√3/2√2)
=(√3+1)/(2√2)=(√6+√2)/4
sin105°=sin(60°+45°)=sin60°・cos45°+cos60°・sin45°
=(√3/2)(1/√2)+(1/2)(1/√2)=(√3/2√2)+(1/2√2)=sin75°
sin105°=sin75°に気が付いて調べると補角公式というそうだ。(全く覚えてないが、高さは一緒だからだなw)
sin105°=sin(180°-75°)=sin75°
sin120°=sin(180°-60°)=sin60°
sin135°=sin(180°-45°)=sin45°
sin150°=sin(180°-30°)=sin30°
三角関数の加法定理 cos
cos(A+B)=cosA・cosB-sinA・sinB
cos(A-B)=cosA・cosB+sinA・sinB
cos15°=cos(45°-30°)=cos45°・cos30°+sin45°・sin30°
=(1/√2)(√3/2)+(1/√2)(1/2)=(√3/2√2)+(1/2√2)
=(√3+1)/(2√2)=(√6+√2)/4
cos75°=cos(45°+30°)=cos45°・cos30°-sin45°・sin30°
=(1/√2)(√3/2)-(1/√2)(1/2)=(√3/2√2)-(1/2√2)
=(√3-1)/(2√2)=(√6-√2)/4
これも補角公式があるそうで・・
cos105°=cos(180°-75°)=-cos75°
cos120°=cos(180°-60°)=-cos60°
cos135°=cos(180°-45°)=-cos45°
cos150°=cos(180°-30°)=-cos30°
マイナスが付くのは底辺が逆向きだからかな?w
補角公式や加法定理は「ウィキペディアの三角関数」のページ、大学受験対策の三角関数については「高校数学の基本問題の三角関数の加法定理,倍角公式,3倍角公式,半角公式」のページを参考にして欲しい。
息子の数学のレベルが低い話を妻としていると、高校数学の塾へ通っている娘曰く『「15°と75°の2つだから三角関数の値は暗記しろ」って塾の先生が言ってたよ」だそうだ。それと補角公式で足りるってことだ。
息子へ電話して「おめぇは今まで何を勉強してんだ!全然足りねぇじゃねぇか!!!」と叱る私。親が足りないから子が足りなのだが、悔しいったらありゃしない。(大恥w)
私、メンカームの別解答
上の方法で解けなくてやった別の解法。cosAの値に見覚えが無いのでcosBの値から角度を調べようとした。
b2=a2+c2-2ac・cosB
(2√3)2=(3+√3)2+(√6)2-2(3+√3)・√6・cosB
2(3+√3)・√6・cosB=(3+√3)2+(√6)2-(2√3)2
2√6(3+√3)・cosB=
cosB=(6√3+6)/(2√6(3+√3))=(6
=6/(2・√2・√3・√3)=1/√2
点Aから辺BCの垂線を引き、辺BCとの交点をDとする。
BD=AB・cosB=√6×(1/√2)=√3
DC=BC-BD=3+√3-√3=3
cosB=1/√2 より ∠B=45°
AD=AB・sinB=AB・sin45°=√6×(1/√2)=√3

cos∠BAD=AD/AB=√3/√6=1/√2
∠BAD=45°
cos∠CAD=AD/AC=√3/(2√3)=1/2
∠CAD=60°
∠A=∠BAD+∠CAD=45°+60°=105°

答え ∠A=105°
JIMMYさんから頂いた解答
大学入試という事なので、じっくり解法ではなく、高速解法でやってみます。所要時間1分。
AからBCに垂線を下ろし交点をDとします。三平方の定理で
三角形ABDはBD^2+AD^2=AB^2=6、三角形ADCはCD^2+AD^2=AC^2=12
※BCは3+√3ですが、BD=√3、DC=3のようですね。
そうなるとAD=√3だから
三角形ABDは直角二等辺三角形なので∠BAD=45°
三角形ADCは正三角形を半分にした形なので∠CAD=60°
∠BAC=45+60=105°です。
※は瞬間的に閃くと解くのが速くなります。

メンカームのコメント
先ずはいつも協力して下さるJIMMYさんへ感謝!m(_ _)m
ピタゴラスの定理を利用して解いてあり、この方法なら中学生でも解ける。
私がもう少し細かく解説しよう。

BD=x、AD=h とする。
三角形ABDについてピタゴラスの定理の式を作ると
AB2=BD2+AD2
(√6)2=x2+h2 ---①
三角形ACDについてピタゴラスの定理の式を作ると
AC2=CD2+AD2
(2√3)2=(3+√3-x)2+h2
x2+h2+6√3-2√3x-6x=0
①よりx2+h2=(√6)2なので
(√6)2+6√3-2√3x-6x=0
(6+2√3)x=6+6√3
x=(6+6√3)/(6+2√3)=(6(1+√3))/(2√3(1+√3))=3/√3=√3
①より
(√6)2=x2+h2
6=3+h2
h2=3
h=√3
DC=BC-BD=3+√3-√3=3

三角形ABDの辺の長さの比は AD:BD:AB=√3:√3:√6=1:1:√2 なので、
三角形ABDは、直角二等辺三角形の三角定規(45°45°90°の角をもつ)と相似。
よって∠BAD=45°
三角形ACDの辺の長さの比は AD:AC:CD=√3:2√3:3=1:2:√3 なので、
三角形ACDは、正三角形を半分にした直角三角形の三角定規(30°60°90°の角をもつ)と相似。
よって∠CAD=60°

∠A=∠BAD+∠CAD=45°+60°=105°
答え ∠A=105°
大学入試対策問題集からの設問だが、中学生が知っているピタゴラスの定理で解けた。\(^o^)/
もう数学はエエよと否定的な声が聞こえそうだが、中学生向けのサマーコムカニッタサー問題集より今週の1問。(シリーズ化か?w)
問題集の模範解答を見ても意味が分からなかった問題。私は別の方法で解いた。
問 四角形LMNAの面積を求めなさい。(誤記修正しました。m(_ _)m)

タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
タイの高校生向け数学入試問題の記事へのリンク→#大学入試
貴方のクリックとコメントが、このブログのパワーの源です。
下の2つのバナーへ応援クリックをお願いします。
 海外生活ブログ タイ情報 人気ランキングはこちら
海外生活ブログ タイ情報 人気ランキングはこちらリアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。
 タイの人気ブログが大集合!!
タイの人気ブログが大集合!!登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。


















