 タイでヒモ暮らしな私の家庭内の役割は子育てが主な事もあって、ネットでも教育関連の記事を興味を持って読むが、日経ビジネスのオンラインゼミナール「僕らの子育て」へ「AI時代、子育てで最強の「習い事」は何だ?」という記事があり、私がピンと来た部分を引用したので、先ずは読んで欲しい。
タイでヒモ暮らしな私の家庭内の役割は子育てが主な事もあって、ネットでも教育関連の記事を興味を持って読むが、日経ビジネスのオンラインゼミナール「僕らの子育て」へ「AI時代、子育てで最強の「習い事」は何だ?」という記事があり、私がピンと来た部分を引用したので、先ずは読んで欲しい。AI時代、子育てで最強の「習い事」は何だ?子どもの習い事を決める時に、大切にすること。それは、その習い事を子どもが楽しいと思うかどうかです。楽しいと思わないと続きません。
僕は今は大学生になった娘が小さい頃、ゴルフを習わせようと思いました。普通、ゴルフスクールというと、練習場に行って、ルールを覚えて、一生懸命打って……という流れで日本では教えるのではないでしょうか。
けれど米国で同じように教えようとすると、「練習させてうまくさせることは親の仕事ではないですよ」と怒られたんです。子どもにそんなことをしても、ゴルフを嫌いになるだけだから、と。それよりも、ゴルフ場を走らせたり、バンカーの砂場でお城を作らせたり、ボールを手で投げさせたり。まずは「ゴルフ場=楽しい場所」という経験をさせましょう、ということでした。
サッカーでも水泳でも一緒で、勝つために頑張るというのは、好きになればやるようになるのだと思います。大切なのは、どうやって子どもにそれを好きにさせるか。言い換えれば、いかに「課外活動=楽しい、好き」という脳の条件反射をつくるのか。それが親の腕の見せどころだと思います。
お小遣いなどの報酬を与えるのが効く子もいれば、親が一緒に楽しむことが効く子もいるはずです。僕の場合は、そのスポーツを一緒に見に行って、「プロの試合はすごいね」と言ってみたり、テレビで試合を一緒に見たりしながら、「この選手、すごいよね」というコミュニケーションを自然につくっています。
記事では「習い事」について話して居られるが、そのまま「習い事」を「勉強」へ入れ替えても同じだろう。
私は勉強嫌いで、学校の授業は退屈なのでずっと寝ていたが、科学には興味があり、図書館へ行ってはそういう分野の本をよく読んだ。科学が好きになった切っ掛けは、幼稚園の年長組の時に母が作って見せてくれた車のプラモデル。電池とモーターで走行可能であり、しばらく遊んだ後にモーターを分解して中を引き出した記憶がある。それからタミヤの楽しい工作シリーズのパーツを使って車を作ったりして楽しみ、小学の高学年になると電子工作。中学生でアマチュア無線、パソコン・・・と興味の対象が少しずつ変化し、大人になってそういう分野が仕事になると、自然や生き物が面白くなった。
娘の勉強も、最初は14という数の意味が理解できないところから始めたが、コインを使ってクイズ形式で遊びながら教え、そこから問題集を活用した学習も始め、頑張ったらご褒美付きで「全問正解セブン旅行」と自転車でセブンへ買い物へ行ったりと、甘く甘くやって一緒に遊んでいた。私も楽しんでいたが、あの頃の勉強は遊んでいるみたいで、勉強している気がしなかったと娘も言っている。
中学生になった今は昔のように遊びながらは勉強しないが、それでも娘は勉強が好きで面白いらしい。「勉強=楽しい、好き」という脳の条件反射が出来上がっているのかも?
いま大学生な息子が小さい時は、好きな玩具を買い与え、家中をプラレールが走り回ったり、市販のラジコンを改造して公園で走らせたりとよく遊んだが、勉強は全部学校任せ。タイへ来てからは小学校のランクアップ転校に良い成績が必須ということもあって私が教えたが、小3くらいだと遊びながら教えるなんてやらないので、何度も同じ場所を間違えると叱ったりで、決して楽しくなかっただろう。
この影響は後々まで続き、大学受験で数学の成績が悪いので教えようとしても逃げ回って拒否。「私との勉強=楽しくない、嫌い」という脳の条件反射が出来上がっていたのだろう。大手塾の模試が最悪で落ち込んでいる時に、問題を解いて見せてようやく受け入れて貰ったが、高3になって教えても、小学校から積み上げた物が教科書レベルしかないのが悲しかった。
親や祖父母等の親族が教えるのは、親側には大きな期待があり、子供側には遠慮が不要な甘えもあって、「教師でも我が子へ教えるのは難しい」という話もあるくらい。引用した記事を見ても小さい時が大切で、勉強や習い事を「楽しい・好き」と印象付け出来ないなら、「楽しくない・嫌い」となるより、関与しない方が良いのかも知れない。
ウドンタニで人気のいくつかの塾でも、お菓子やお小遣いを準備してゲーム形式で競わせるように教えている。ゲームへ積極的に参加する子は驚くほど早く伸びるが、無関心な子はさっぱり無駄になるので、入塾の申し込み時に目を見て話せなかったり、落ち着きがない子は排除される所もある。
娘が通っている英語塾は高校生以上向けのコースへ入れて頂いているが、やはり知っている単語を競わせたりで、毎回ゲームが有るそうだ。娘のライバルはD校のおかまちゃん。ずっとクラスで2位が続いていたが、先日やっと優勝だと言うので、何で競ったか尋ねると国の英語名。学校の地理の授業でアフリカの国を全部覚えるのをやったばかりだったそうで、アフリカの国名を連発して勝ち抜いたそうだ。子供向けコースではないので、景品も賞金も貰えないが、ゲームとなると燃えるらしい。これも条件反射が脳へ組み込まれているのかも?w
さて、数学へ入ろう。
前回の問題

直線ABと直線CDの交点をMとすると、3AM=4MB 3CM=MD となり、
直線ABの長さは14、∠ABDと∠ACDの角度が等しい時のCMの長さを求めなさい。
第3回IJSOの一次試験問題より引用

直線ABと直線CDの交点をMとすると、3AM=4MB 3CM=MD となり、
直線ABの長さは14、∠ABDと∠ACDの角度が等しい時のCMの長さを求めなさい。
第3回IJSOの一次試験問題より引用
教科書的に真っ直ぐ解いた解答
教科書的に2つ三角形の相似を利用して解いてみる。(塾技数学100 塾技56)
先ずは設問から図を書くと・・・

こんな風に書けるだろう。
設問より∠ABD=∠ACDであり、対頂角なので∠AMC=∠DMB。
三角形の2つの角が等しいので、⊿MAC∽⊿MDB。(相似)
判り易く2つの三角形を並べて書いてみる。
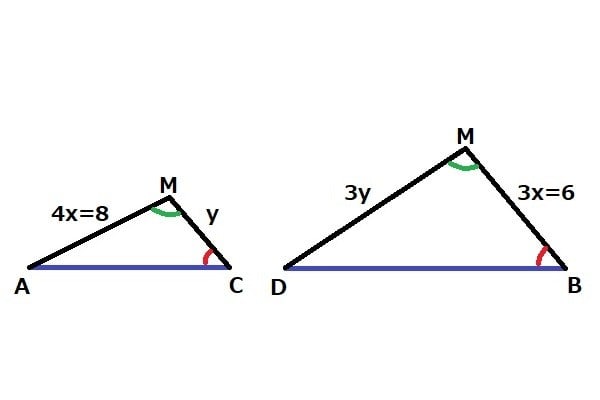
MA:MD=MC:MB
8:3y= y:6
3y2=48
y2=16
y=4
CM=y=4
答え 4
#相似 #辺の比 #中学数学
面積比を利用した解答
日本の中学受験参考書「塾技算数100」で紹介されている「1組の角が等しい三角形の面積比は、その角を挟む2辺の長さの積の比と等しい(塾技67)」を利用して解く。
先ずは設問から図を書くと・・・

こんな風に書けるだろう。
設問より∠ABD=∠ACDであり、対頂角なので∠AMC=∠DMB。
三角形の2つの角が等しいので、⊿MAC∽⊿MDB。(相似)
判り易く2つの三角形を並べて書いてみる。

⊿MACと⊿MDBの面積比は、等しい角を挟む2辺の長さの積の比と等しいので、
⊿MAC:⊿MDB=4x・y:3x・3y=4xy:9xy=4:9
面積比が4:9の相似な図形の辺の長さの比は、√4:√9=2:3。
CM=(2/3)BM=(2/3)・6=4
答え 4
#辺の比 #面積比 #中学数学
方べきの定理を利用した解答
日本の高校受験参考書「塾技数学100」で紹介されている「円と円周上に無い点があり、円周上に無い点を通る2直線と円周が交わる時、円周上に無い点と円周上の2点までの距離の積を方べきと言い、方べきの値は一定となる。(塾技66)」を利用して解く。
先ずは設問から図を書くと・・・

となり、設問より∠ABD=∠ACDなので、「一つの弧に対する円周角の大きさは一定」という円周角の定理(塾技数学100 塾技63)よりA・B・C・Dは同一円周上にあるのが判る。

方べきの定理より AM・BM=CM・DM なので、
8・6=y・3y
48=3y2
y2=16
y=4
CM=y=4
答え 4
#方べきの定理 #中学数学
日本とタイでは出題傾向が異なるので全部はカバー出来ないが、タイで高校受験までの図形の勉強をさせるなら、日本の中学受験参考書「塾技算数100」と高校入試参考書の「塾技数学100」は、お薦めの参考書だ。タイの参考書へ書かれているのは教科書的な解法が多く、日本の至れり尽くせりで痒い所へ手が届きまくりな参考書を使えるのは日本語が読める人の特権(w)と言っても良いだろう。
次の1問

半径6の内接円を持つ台形の、上底の長さが7で下底の長さが21の時に、脚(縦長の2つの辺)の長さの差を求めなさい。

半径6の内接円を持つ台形の、上底の長さが7で下底の長さが21の時に、脚(縦長の2つの辺)の長さの差を求めなさい。
設問へ図は無いが、解り難いので図を入れると下のようになる。
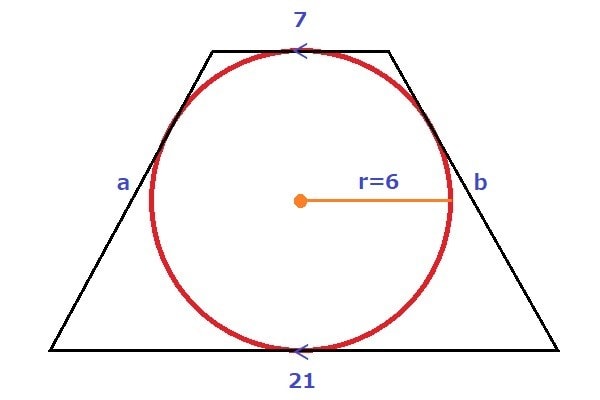
脚をそれぞれaとbとした時に|a-b|が求める答えとなる。
ムガさんのとこのお兄ちゃんに2問連続で簡単に答えられたので、今回は少し難しい問題にした。w
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
貴方のクリックとコメントが、このブログのパワーの源です。
下の2つのバナーへ応援クリックをお願いします。
リアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。
登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。




















勉強に対する意識ですが、私は元々勉強が出来ないし嫌いでしたから、
その頃の私が紹介した記事を読めば、何を言ってんだと思うかも知れませんが、
タイで暮らして、子供を進学校へ入れ、上位の子供を目にする様になりますと、
我が子との素養の違いや親の接し方、環境の違いも少しずつ判ってきました。
私が見ていると確かに全国で上位へ行くような子供は天才的な素質を持っていると思いますが、
天才的な素質を持ちながらも、その力を発揮できずに低迷している子供は多いですし、
天才的な素質が無くても、県内で上位をキープする子供の大部分は普通の子供です。
学力の違いの原因が何かと言いますと、やはり環境。
子供の学習を親がどれだけサポートするかが鍵ではないでしょうか?
子育てと植物の栽培は、同じ生物ですから似ているでしょうね。
子供は野菜。確かにそうかも知れません。
私も自然農で育ちましたw。
好きな事に没頭できて良かったと思うこともありますが、
大学受験のどうにもならない悔しさを思い出すと、
子供を同じ目に遭わせたくないという気持ちも強いです。
私が気が付くのが遅くて、息子は間に合いませんでしたが、
娘は何とかしたいと頑張ってます。
出来る力を持たせた上で、娘の好きに将来を選んで欲しいです。
mugaさん
ネットへは寮がある私立の一覧とかありまして、探すのは簡単でした。
福岡で寮がある私立で一番偏差値が低いのは42です。
私が思うに、お嬢さんは日本語の壁を乗り越える途中でして、
既に驚くような成果は見えてますから、
帰国子女枠とか、入りやすい方法もあるのではないでしょうか?
お兄ちゃんの解答ですが、正解です。
今回の設問は円の接線の知識とピタゴラスの法則で解けますが、
解答途中に小細工がいくつか必要で、難しい問題だと思います。
恐らく同様な問題の経験があるのだろうと思いますが、
よく頑張って勉強されていると思います。これはバンコクの高校へ行っちゃいますよ!
次の記事へ解答を掲載しますが、
もっと簡単な解き方が有ったら教えて下さいね。
21-7=14なので、底辺の両側を直角三角形に見立てて片方をZだとすると反対側の底辺は14-Zになると。
で、高さは6×2=12なので、ピタゴラスにて台形両側の辺の長さが出たそうです。
どうやってそれに気付いたんだ?と質問すると
社会の授業中に眠たくなっちゃって、眠らないように朝もらった計算を考えてたら突然閃いたんだ!
だそうですが、
だとすると、やっぱり7分ではないですwww
姉が福岡女学院の過去問を購入して娘に見せたところ
最初の問題で「あ、これイヤ」と言ってパタンと閉じたそうです。
確か、そこも偏差値は高くはなかったはずですが
山口では49~47ですか、、、拒絶反応がありそう(T-T)
一昨年だったか、ビリギャルのDVDを購入してあげましたが、母親の家で何回も見せられて飽き飽きしてたらしいのですけど、今回の里帰りで思い出させようと思って内容を話し掛けました。
あの彼女、はじめは聖徳太子が読めなかったんだぜ!
「あ、知ってる知ってる、せいとくタコ!」って言ったよな。
それが娘の笑いのツボに刺さったのか大爆笑ですもんね、やっとギャグの意味が理解できたようですww
千里の道も一歩から?
あ、今回の問題ですが、かなり長い計算式を書いてます。苦戦したようですよ、本人は7分だとかほざいてますが、たぶん15分はやってるはずです。答えは2だそうです。いつも有り難うございますm(__)m
貧乏人の悲しさ。
コメント4件
参考になった4人(28%)
参考にならなかった10人(71%)
日本の園芸農業みたいに思った。
子供は野菜よねって。
うちは自然農に近いかなあ。
世の中へハウツー本は溢れてますが、誰もが簡単に再現できるなら苦労しないし、
お金を出して本を買う人も居ないでしょう。
仰るように机上で考えた集大成であったりで、現実が無視されているのもあるでしょうし、
子供が育つ環境も、子供の性格も千差万別で同じではありませんから、
再現しろと言うのが無理かも知れません。
親の意を汲もう、親を喜ばそうと自我を殺して頑張る子供の話もありますね。
子供が装飾や見栄晴ツールもあるでしょう。
小さい時は着飾って猫可愛がりして、ある程度育って可愛くなくなったらポイってのは
身近に見ましたよ。
幕末から明治維新に掛けて日本の近代化に貢献された方々は大変だったでしょうね。
私がウドンタニの子供達を見ても、上位を目指す子供達はそういう感じです。
日本だと体系的に整理された参考書がいくらでもありますし、
ネットで無料で教える動画も多いですが、
タイでは「これだ!」と言える本が見つかりませんし、
使えるレベルの無料動画も無ければ、塾も僅か。
その中であの手この手で知識を得て実力を伸ばしてます。
うちの娘はさっぱりですが、頑張る子供達の姿は感動的でさえあります。
我が娘をその中へ放り込んでやろうと、私も頑張ってます。
先ずは「好きこそ物の上手なれ」ですw。
mugaさん
勉強は多数の子供達にとって苦痛だと思いますが、
それを喜んでやっている子供が居るって話です。
そして「好きこそ物の上手なれ」を実行。
子供もいろいろですから、その方法に乗れない子供(私w)も居る訳で、
別の方法が見つかれば良いですが、やはり楽しんで勉強している子に勝つのは難しいでしょうね。
私は学校の勉強が嫌いでしたが、別の分野では他人が苦手な事が好きだったりで、
時間が経つのを忘れて深夜まで没頭したりでした。
嫌いなことをやれと言われても出来ませんから、自分へ向いた何かが見つかれば良いのかなと思います。
自分が学生の時にあれだけ嫌いだった算数も今は面白いですから、
面白さに気が付かなかっただけかも知れませんね。
そういうところを親がサポートして、面白く出来たらって思いますよ。
娘の場合は年上と競争して凹ますのが面白いみたい。親に似て性格悪いですね。
先日も英語のコース修了試験で、古株のオカマな高校生を撃破したそうで、
「1人褒められて、ほら表彰状!」と大興奮で迎えの車へ飛び込んで来ました。
停滞している数学でもその興奮を引出してやろうと、賞金を考えているところです。
お兄ちゃんは解答を楽しみにして下さっているそうで、嬉しいです。
娘が解けなかった中から面白い解き方を選んで掲載しますので、お相手下さい。m(_ _)m
お嬢ちゃんも順調に成長され、ご自分から教材を欲しがられたそうで、素晴らしいですね。
勉強の「好き」と「出来る」のどっちが先ですが、
娘が幼稚園の時は、出来ない時にもう一度教えて出来たらOKとかハードルを低く低く設定して、
失敗してもやり直せば、成功するって感じで、やれば出来る状態から始めて、褒め殺しw。
幼稚園児に長時間の勉強は出来ませんし、
家で遊ぶったって自分が幼稚園の時も女の子相手にままごとは嫌いでしたから、
ご褒美買いに行こうと連れ出して、セブンへ行って、公園で食べてと連れ回して帰ったらお昼寝w。
それで喜んでくれてましたから、私は「好き」が先だと思います。
日本の習い事では楽しむのは二の次で、武道の延長みたいなノリを引きずってますからね、
努力と根性、またチームワークで達成感を感じて成長するのが目的みたいになってますかね?
それはそれで、ノリに付いてこれる子には楽しい場所なのでしょうけど、そうじゃない子には苦痛って事もありますね。
運営者の資質や方針により、合致すれば楽しくできる習い事はあるでしょう
でも一般的には「楽しい=成長しない」ですから、ある程度のストレッチや苦しみは必要かと思います。
私のケースでは運動部=地獄だったのですけど、ま、あれで散々虐められて根性を鍛えられたから、その後の荒波に対応できた気もします。
で、勉強の方でも教える方の資質や情熱、またプログラムによっては楽しく行えるかもしれないし、子供が勉強を大好きになる可能性はゼロではないかもしれませんが、やっぱり楽しいってのは、後からくる達成感だけで良いのではないかと思いますね。
お嬢ちゃんの場合はライバルに勝つという目的をモチュベーションにすることにより達成感をゲットできるエンジンになってますね。
うちの息子にもそんなエンジンがあれば、夜な夜なイタズラ動画を見て大爆笑する時間も惜しんで机にカジリつくはずです。
ライバルに勝つなんて意識はゼーンゼンありませんが、メンカームさんからの問題にはヤル気が刺激されるようで「答えはまだ?」と毎日聞いてきますw
また娘は歴史人物カルタを買ってくれと伯母ちゃんにお願いしたらしくて、そんな自主的な姿勢は初めてだと涙目で喜んでくれましたが、それって単に楽しむ事を優先してるだけです。
でも娘のレベルでは、そうでもしなくちゃ総拒否になっちゃうので致し方なし(x_x)
しかし勉強が好きな子って、勉強ができるから好きなんだと思いますけど、その勉強ができる子は勉強が好きだから頑張れたのでしょうし、
なんだか卵が先か鶏が先かってくらいにクラクラしますね(-_-;)
好きなんだ、と見せかけても、子供は実は、多分敏感で、それが演技だと結構わかっている、それでも、気持ちも理解できるから、遣っている内に、楽しくなるという事も有るだろうけれど。
本当に好きな事、真剣に考えている事だけで、相当の部分は宜しいかと、後、別件でも、誰も見ていないところで、真摯な態度で遣っているのが、薄々伝わる事でも効果は有りそう。
子供が、自分を飾る装飾品や見栄を張るためのペットだと思われたら、万事休す、って感じじゃなかろうかと思っています~~♪
勉強も、子供の段階でも、効果を高めるのはご褒美だったり激励だったり、色んなお話だったり、色々有るでしょうが・・幕末~明治に色んな所で、活躍した人たちで、今で言う、体系的学問をした方は殆ど居なくて、主に支那も含めて古典や歴史書を読んで居て、人格は育てられていたが、実学はそれほどでもなかったようだが、もともと能力の高い人々だったから経験しながら、都度、対応していた風・・
そう言う意味では、ここの登場主役は、素晴らしい。