http://www.kurims.kyoto-u.ac.jp/~ooura/fft-j.html
例のC言語用FFTライブラリを、実際に弄って、パラメタ
の指定の仕方によって、意図した結果が得られるかを
確認してみることに。
いろいろ探ってみると、
http://geisterchor.blogspot.jp/2011/04/fft_16.html
こちらに、例のFFTライブラリを使ってみた結果がリポート
されているので、その情報を頼りに、Ubuntu環境下でgccで
まずは動かしてみることに。
gccを久々に使ったので、コンパイルでいろいろ手間取った。
もともとのライブラリのmakeファイルの中身をすっ飛ばして
使いたかったので、上記のサイトのページで示されている
ヘッダファイルを利用させていただいた。
さくっとコンパイル通るようになった。ありがたい。
このヘッダファイルを使わせていただきつつ、64サンプル
の場合と、256サンプルの場合を使って、あるデータを
ぶっこんだら、想定どおりの結果が出てくるのかを確認
してみる。
まず、実験に使ったプログラム。64サンプルから。
上記のサイトのプログラムでは、mallocで配列のエリアを
確保してるんだけど、出来ればmalloc使わずに済ませたい
ので、固定サイズで割り当てするように変えたりとか、
いろいろ弄って、最小限のコンパクトなプログラムに
したのがこれ。
(例によって、このブログの仕様により、include文など
の不等号マークを全角文字に置き換えてあります)
// gcc fftsg.c myfft64.c -lm -o myfft64 //
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "./fftsg.h"
#define FS 6400 // サンプリング周波数
#define LEN 64 // 信号長 == FFT点数
#define N (LEN * 2) // データ個数(実数、虚数)
#define F0 500 // 正弦波周波数
void outdata (char *title, double *a) {
int i;
printf("%s\n",title);
printf("No , real , imaginal , log10\n");
for (i=0; i<LEN; i++) {
printf("%d , %f , %f , %f\n",
i, a[i*2], a[i*2+1],
10.0*log10(a[i*2]*a[i*2] + a[i*2+1]*a[i*2+1]) );
}
printf("\n");
}
int main () {
int ip[8 + 2]; // sqrt(64) + 2
double a[N]; // points * 2
double w[LEN]; // points
int i;
// generating data
for (i = 0; i < LEN; i++) {
a[i*2] = sin(2.0 * M_PI * i * F0 / FS);
a[i*2 + 1] = 0.0;
}
/* display original data */
outdata("*** input data ***", a);
/* do fft */
ip[0] = 0.0;
cdft(N, -1, a, ip, w);
/* output result */
outdata("*** fft result ***", a);
}
プログラム中の、配列「a」に初期値としてぶっこんでる
正弦波が、FFTを掛けたいデータ。実数→虚数の順に、
64組のデータを入れておけば、FFTがかかる。
(通常に使うときは、実数のところにADCのサンプリング
データを入れて、虚数のところに0を入れておけばok)
結果は、標準出力に出してるので、これをパイプでファイル
に繋ぎ換えて、表計算ソフトでグラフにする。
入力データ。サンプリング周波数6400sps、データの正弦波
は500Hzという前提で、64サンプル分。青が実数、橙が虚数。

FFT掛けた結果。

左下のとんがりが、正の周波数分の出力。ちょうど500Hzの
ところにピコンと立つ。
右上のとんがりは、負の周波数分。
これらのデータを、実数、虚数それぞれを平方和して
平方根とれば、各周波数成分の量がわかる。
さらに256サンプルも試してみる。
プログラム。ほとんど同じだけど、定数だけ調整。
// gcc fftsg256.c myfft.c -lm -o myfft256 //
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "./fftsg.h"
#define FS 6400 // サンプリング周波数
#define LEN 256 // 信号長 == FFT点数
#define N (LEN * 2) // データ個数(実数、虚数)
#define F0 500 // 正弦波周波数
void outdata (char *title, double *a) {
int i;
printf("%s\n",title);
printf("No , real , imaginal , log10\n");
for (i=0; i<LEN; i++) {
printf("%d , %f , %f , %f\n",
i, a[i*2], a[i*2+1],
10.0*log10(a[i*2]*a[i*2] + a[i*2+1]*a[i*2+1]) );
}
printf("\n");
}
int main () {
int ip[16 + 2]; // sqrt(256) + 2
double a[N]; // points * 2
double w[LEN]; // points
int i;
// generating data
for (i = 0; i < LEN; i++) {
a[i*2] = sin(2.0 * M_PI * i * F0 / FS);
a[i*2 + 1] = 0.0;
}
/* display original data */
outdata("*** input data ***", a);
/* do fft */
ip[0] = 0.0;
cdft(N, -1, a, ip, w);
/* output result */
outdata("*** fft result ***", a);
}
入力のデータ256サンプル分。

サンプル数が4倍になっているので、取り込まれている波の
数も4倍になっている。(サンプル周波数6400spsとデータ
となる正弦波の周波数500Hzはおなじまま)
結果は、こう。
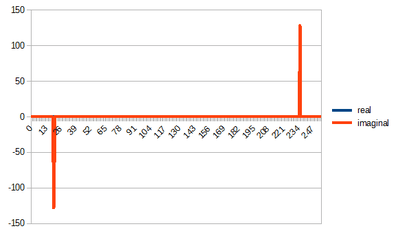
周波数分解能が高くなってる分、とんがりが細くなってる。
けど、当然ながら500Hzのところにピコンと立ってる。
うん。できた。普通にFFTができる。ただ、このライブラリ
には、窓関数の処理が付いてないので、その辺は独自に処理
する必要有り。
キリのいい周波数じゃないと、窓掛けずにFFTすると、
エンベロープが広がってしまうのは、普通のFFTといっしょ。
というわけで、どこにどんなパラメタを指定すれば、
どんな結果になるのかは判った。
あとは、この浮動小数点処理のまま、mbedにぶっこんだら、
十分な処理速度で処理できるのかが問題かな。
うちにあるSeeeduino Archは、FPUなんて搭載してなかった
よなぁ。たしか。
あと、平方和の平方根も、FPUなしで処理すると、すんごい
時間かかるんだよな…
Nulceoシリーズで、FPU搭載してる(かつmbedで有効化が
されてる)のって、あるのかなぁ?
できればやっぱ、整数処理にして、開平なんかもテーブル
処理したいところなんだけどな。
ArduinoのFFTライブラリは、その辺よく出来てるんだよな。