今まで Metis ライブラリは、SDPA 用に Sparse Matrix Reordering Programs を解くためにしか用いていなかった(ただしSDPA 7.1.1 では Spooles ライブラリのみを Matrix Ordering を決めるために用いている)。しかし別の研究でグラフの k-分割問題を解く必要が出てきたので、グラフ分割問題用に Metis ライブラリを用いることにした。
この場合の目的は以下のように定義されているので、点にファイル容量などの重みが付いている場合にも対応できる(点の重みは複数も可)。
the objective of the partitioning algorithm is to minimize the edgecut subject to the constraints that each one of the m weights is equally distributed among the domains.
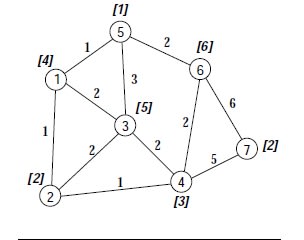
マニュアルの 16 ページにある例題だが、グラフは添付の図のように、データは以下のように定義されている。
7 11 11
4 5 1 3 2 2 1
2 1 1 3 2 4 1
5 5 3 4 2 2 2 1 2
3 2 1 3 2 6 2 7 5
1 1 1 3 3 6 2
6 5 2 4 2 7 6
2 6 6 4 5
Metis make 後に pmetis を用いて上記のグラフを二分割する。
./pmetis test.graph 2
**********************************************************************
METIS 4.0.1 Copyright 1998, Regents of the University of Minnesota
Graph Information ---------------------------------------------------
Name: test.graph, #Vertices: 7, #Edges: 11, #Parts: 2
Recursive Partitioning... -------------------------------------------
2-way Edge-Cut: 5, Balance: 1.04
Timing Information --------------------------------------------------
I/O: 0.000
Partitioning: 0.000 (PMETIS time)
Total: 0.000
**********************************************************************
(1,2,3,5) と (4,6,7) に分割されて Edge-Cut は 5 となる。点の重みの合計は 12 と 11 になっている。試しに点 5 と 6 の重みを交換してみる。
**********************************************************************
METIS 4.0.1 Copyright 1998, Regents of the University of Minnesota
Graph Information ---------------------------------------------------
Name: test2.graph, #Vertices: 7, #Edges: 11, #Parts: 2
Recursive Partitioning... -------------------------------------------
2-way Edge-Cut: 8, Balance: 1.13
Timing Information --------------------------------------------------
I/O: 0.000
Partitioning: 0.000 (PMETIS time)
Total: 0.000
**********************************************************************
今度は (1,5) と (2,3,4,6,7) に分割されて Edge-Cut は 8 で点の重みの合計はそれぞれ 10 と 13 になる。卒業論文のときにはグラフ分割問題を扱ったこともあるが、なかなか楽しいソフトウェアになっている。
この場合の目的は以下のように定義されているので、点にファイル容量などの重みが付いている場合にも対応できる(点の重みは複数も可)。
the objective of the partitioning algorithm is to minimize the edgecut subject to the constraints that each one of the m weights is equally distributed among the domains.
マニュアルの 16 ページにある例題だが、グラフは添付の図のように、データは以下のように定義されている。
7 11 11
4 5 1 3 2 2 1
2 1 1 3 2 4 1
5 5 3 4 2 2 2 1 2
3 2 1 3 2 6 2 7 5
1 1 1 3 3 6 2
6 5 2 4 2 7 6
2 6 6 4 5
Metis make 後に pmetis を用いて上記のグラフを二分割する。
./pmetis test.graph 2
**********************************************************************
METIS 4.0.1 Copyright 1998, Regents of the University of Minnesota
Graph Information ---------------------------------------------------
Name: test.graph, #Vertices: 7, #Edges: 11, #Parts: 2
Recursive Partitioning... -------------------------------------------
2-way Edge-Cut: 5, Balance: 1.04
Timing Information --------------------------------------------------
I/O: 0.000
Partitioning: 0.000 (PMETIS time)
Total: 0.000
**********************************************************************
(1,2,3,5) と (4,6,7) に分割されて Edge-Cut は 5 となる。点の重みの合計は 12 と 11 になっている。試しに点 5 と 6 の重みを交換してみる。
**********************************************************************
METIS 4.0.1 Copyright 1998, Regents of the University of Minnesota
Graph Information ---------------------------------------------------
Name: test2.graph, #Vertices: 7, #Edges: 11, #Parts: 2
Recursive Partitioning... -------------------------------------------
2-way Edge-Cut: 8, Balance: 1.13
Timing Information --------------------------------------------------
I/O: 0.000
Partitioning: 0.000 (PMETIS time)
Total: 0.000
**********************************************************************
今度は (1,5) と (2,3,4,6,7) に分割されて Edge-Cut は 8 で点の重みの合計はそれぞれ 10 と 13 になる。卒業論文のときにはグラフ分割問題を扱ったこともあるが、なかなか楽しいソフトウェアになっている。