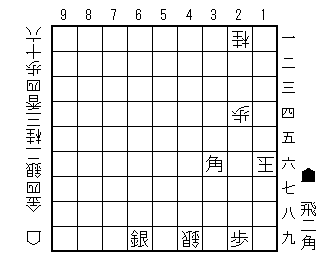
問題図のみ見たい方はこちらへ
答え: 1五飛 2六玉 4八角 3六玉 2六飛 4七玉
4四飛 3八玉 2八飛 まで9手詰め
解説:
「玉方2一桂配置」はいくつかの余詰め筋を防いでいる駒である。
たとえば「2一桂」が置いてなかった場合、「問題図」から1三飛、2六玉、1五飛成以下の「余詰め」が発生してしまう。
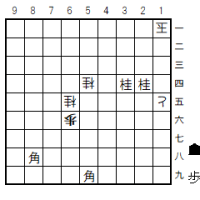
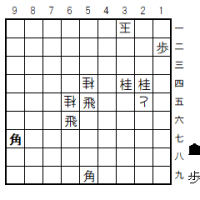
さて、この「問題図」を見て、とりあえず指してみたくなる手は「初手2七角打」であろう。
しかしそれは、2六玉で詰まない。
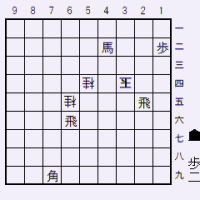
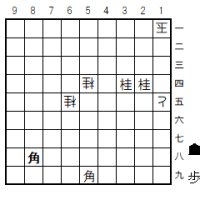
他に解説すべき紛れ筋として、「初手1七飛」がある(次の図)
 紛れ図
紛れ図
この1七飛(図)を、同玉なら、3四角と打ってこの玉は詰む。
しかし、1七飛に、2六玉と応じられて詰まない。以下1六飛打は3四玉と逃げられてしまい、また5三角と打つのは3六玉でこれも捕まえられない。
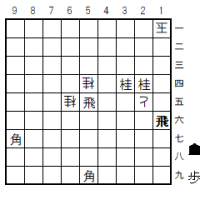
 途中図1(1手目1五飛まで)
途中図1(1手目1五飛まで)
初手の正解手は、「1五飛」(図)である。
これを同玉なら、3七角と打って、以下2六合駒に1四飛まで――というわけ。
よって、1五飛には、玉方は2手目「2六玉」と応じることとなるが、そこでどうする?(次の図)
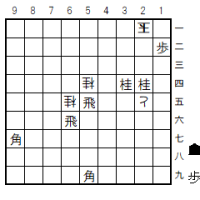
 途中図2(2手目2五玉まで)
途中図2(2手目2五玉まで)
なお、1五飛に代えて1四飛と打つのも考えられるが、2六玉、2四飛、3六玉と進みこの玉は捕まえられない。
攻め方の3手目、ここで2七飛が考えられる。
対して3六玉と角を取りながら逃げれば6三角以下詰む。しかし2七飛に1四玉と飛車のほうを取りながら逃げられて、詰まない。
また、この図で1六飛打は、3七玉と逃げられてしまう。
3手目、正解は、「4八角」である。「3七に逃がさない」という意味だ。
この角打ちは「4八」でなければいけない。(この問題図面、「攻方6九銀配置」は実は「攻方5九歩」でもよいのだが、あえて「6九銀」にして“5九角”と打つ可能性を残し、正解手「4八角」の“限定打感”を少しだが強調させてみた――というのが作者の地味なこだわりである)
「4八角」に対し、3七合駒なら、1六飛打までの詰み。
よって、玉方の4手目は「3六玉」しかない(次の図)
 途中図3(4手目3五玉まで)
途中図3(4手目3五玉まで)
ここまで進めば、あとは簡単。
以下「2六飛」と打って、「4七玉、4四飛、3八玉、2八飛」(次の図)まで、一本道の詰みとなる。
それが正解だが、「玉方2一桂配置」はこの図での3三飛からの余詰め筋も消していることを書いておきたい。
また、この図で1六飛打と、飛車を離して打つと、あとで2八飛と引く手がないので詰まなくなる。飛車打ちは「2六」の限定である。
詰将棋をつくるほうは、解く側の何倍も考えなければいけない。それが楽しくてつくっているわけだが。
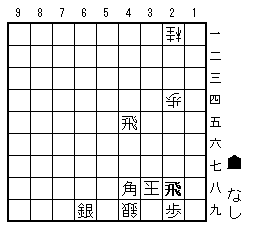 詰め上がり図(9手目2八飛まで)
詰め上がり図(9手目2八飛まで)
これが「詰め上がり図」
2六に打った飛車を、シュッと2八に引いて詰め上げる感覚が気持ち良い。
解説は以上になるが、この詰将棋問題には少し長めの15手詰めバージョンもあるので、それを以下に紹介しておく。
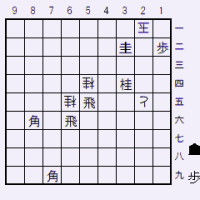
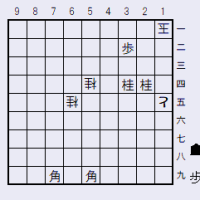
 B案問題図
B案問題図
出題したこの詰将棋は、問題図をこのように改変しても同様の手順で成立する(出題した問題図をA案とし、このバージョンをB案としよう)
このほうが図面がシンプルで見た目は上等だが、手数が6手伸びて15手詰めになる。それをどうみるか。
同じように進めて‥‥
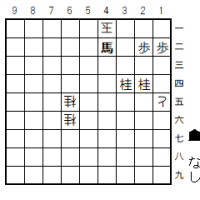
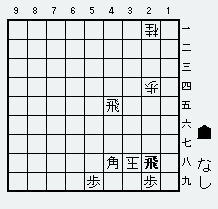 B案途中図
B案途中図
2八飛と引いて、この場合はまだ4九玉と逃げるスペースがあるので“続き”がある(上のA案は「玉 方4九銀」が置いてあった。あの銀は玉方にとって実は“じゃま駒”だったのだ)
以下9三角成、5九玉、4九飛、同玉、4八馬となって―――(次の図)
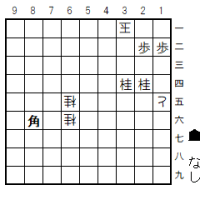
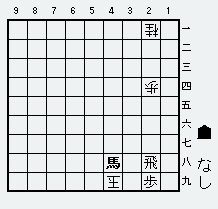 B案詰め上がり図
B案詰め上がり図
これが「B案15手詰め」の詰め上がり図。
これもわるくはないが、A案の、2八飛でピタッと詰めて着地する終わり方が気持ちいいし、解いてもらうには短いほうがよいと思ったので、9手詰めのA案を問題として提出した。
「どっちが良いだろうか」と小さいことで悩むのも、つくる楽しさの一部である。子供がお菓子を食べるときに、赤い菓子から先に食べるか、それとも黄色い菓子から食べるか、真剣に考えているときのような、そんなかんじ。
答え: 1五飛 2六玉 4八角 3六玉 2六飛 4七玉
4四飛 3八玉 2八飛 まで9手詰め
解説:
「玉方2一桂配置」はいくつかの余詰め筋を防いでいる駒である。
たとえば「2一桂」が置いてなかった場合、「問題図」から1三飛、2六玉、1五飛成以下の「余詰め」が発生してしまう。
さて、この「問題図」を見て、とりあえず指してみたくなる手は「初手2七角打」であろう。
しかしそれは、2六玉で詰まない。
他に解説すべき紛れ筋として、「初手1七飛」がある(次の図)
 紛れ図
紛れ図この1七飛(図)を、同玉なら、3四角と打ってこの玉は詰む。
しかし、1七飛に、2六玉と応じられて詰まない。以下1六飛打は3四玉と逃げられてしまい、また5三角と打つのは3六玉でこれも捕まえられない。
 途中図1(1手目1五飛まで)
途中図1(1手目1五飛まで)初手の正解手は、「1五飛」(図)である。
これを同玉なら、3七角と打って、以下2六合駒に1四飛まで――というわけ。
よって、1五飛には、玉方は2手目「2六玉」と応じることとなるが、そこでどうする?(次の図)
 途中図2(2手目2五玉まで)
途中図2(2手目2五玉まで)なお、1五飛に代えて1四飛と打つのも考えられるが、2六玉、2四飛、3六玉と進みこの玉は捕まえられない。
攻め方の3手目、ここで2七飛が考えられる。
対して3六玉と角を取りながら逃げれば6三角以下詰む。しかし2七飛に1四玉と飛車のほうを取りながら逃げられて、詰まない。
また、この図で1六飛打は、3七玉と逃げられてしまう。
3手目、正解は、「4八角」である。「3七に逃がさない」という意味だ。
この角打ちは「4八」でなければいけない。(この問題図面、「攻方6九銀配置」は実は「攻方5九歩」でもよいのだが、あえて「6九銀」にして“5九角”と打つ可能性を残し、正解手「4八角」の“限定打感”を少しだが強調させてみた――というのが作者の地味なこだわりである)
「4八角」に対し、3七合駒なら、1六飛打までの詰み。
よって、玉方の4手目は「3六玉」しかない(次の図)
 途中図3(4手目3五玉まで)
途中図3(4手目3五玉まで)ここまで進めば、あとは簡単。
以下「2六飛」と打って、「4七玉、4四飛、3八玉、2八飛」(次の図)まで、一本道の詰みとなる。
それが正解だが、「玉方2一桂配置」はこの図での3三飛からの余詰め筋も消していることを書いておきたい。
また、この図で1六飛打と、飛車を離して打つと、あとで2八飛と引く手がないので詰まなくなる。飛車打ちは「2六」の限定である。
詰将棋をつくるほうは、解く側の何倍も考えなければいけない。それが楽しくてつくっているわけだが。
 詰め上がり図(9手目2八飛まで)
詰め上がり図(9手目2八飛まで)これが「詰め上がり図」
2六に打った飛車を、シュッと2八に引いて詰め上げる感覚が気持ち良い。
解説は以上になるが、この詰将棋問題には少し長めの15手詰めバージョンもあるので、それを以下に紹介しておく。
 B案問題図
B案問題図出題したこの詰将棋は、問題図をこのように改変しても同様の手順で成立する(出題した問題図をA案とし、このバージョンをB案としよう)
このほうが図面がシンプルで見た目は上等だが、手数が6手伸びて15手詰めになる。それをどうみるか。
同じように進めて‥‥
 B案途中図
B案途中図2八飛と引いて、この場合はまだ4九玉と逃げるスペースがあるので“続き”がある(上のA案は「玉 方4九銀」が置いてあった。あの銀は玉方にとって実は“じゃま駒”だったのだ)
以下9三角成、5九玉、4九飛、同玉、4八馬となって―――(次の図)
 B案詰め上がり図
B案詰め上がり図これが「B案15手詰め」の詰め上がり図。
これもわるくはないが、A案の、2八飛でピタッと詰めて着地する終わり方が気持ちいいし、解いてもらうには短いほうがよいと思ったので、9手詰めのA案を問題として提出した。
「どっちが良いだろうか」と小さいことで悩むのも、つくる楽しさの一部である。子供がお菓子を食べるときに、赤い菓子から先に食べるか、それとも黄色い菓子から食べるか、真剣に考えているときのような、そんなかんじ。
















※コメント投稿者のブログIDはブログ作成者のみに通知されます