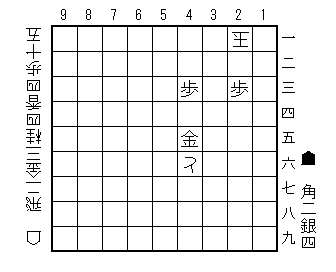
問題図だけを見たい方はこちらにどうぞ
答え: 2二銀 1二玉 1三銀打 2三玉 2四銀打 1四玉
3六角 同と 1五銀打 2六玉 3四角 まで11手詰め
解説:
初手正解手は2二銀。
代えて初手3二銀が紛れ筋。初手3二角もあり、これらの紛れ筋の解説については、最後に示すこととする。
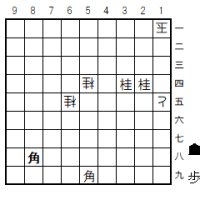
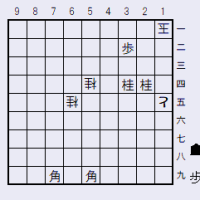
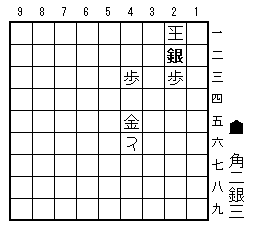 途中図1(初手2二銀まで)
途中図1(初手2二銀まで)
初手2二銀(図)に、3二玉と逃げる手には、3三銀成がある。3三同玉、3四銀、2四玉、3三角以下、11手駒余り詰めとなる。
2手目は、1二玉が正解手となる(次の図)
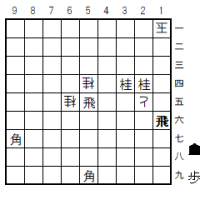
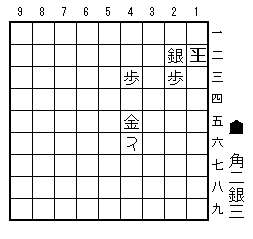 途中図2(2手目1二玉まで)
途中図2(2手目1二玉まで)
ここで1三銀打の“平凡手”が3手目の正解手だが、他の手を考えるとすれば2一角がある。しかしそれは2三玉、3四銀(角)、1四玉となって、この玉は捕まらない。
この「途中図2」から、1三銀打、2三玉とすすめて、次の図になる。
 途中図3(4手目2三玉まで)
途中図3(4手目2三玉まで)
ここで2四銀打と、3四銀、あるいは3四角がある。
しかし「3四」に銀や角を打つ手は、1四玉と応じられてみると、玉を逃がしてしまっている。1五~2六という脱出路を止めることができない。
2四銀打と、ここも“平凡手”にみえるこの手が正解となる。
以下1四玉に、そこで、3六角の好手がある(次の図)
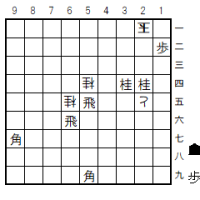
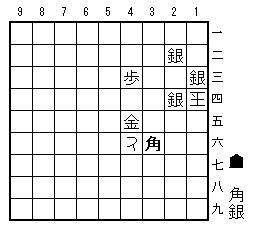 途中図4(7手目3六角まで)
途中図4(7手目3六角まで)
3六角(図)。この手があるので、この玉を補足することができる。同とと取らせて、「3六」への脱出路を塞ぐ。
3六同とに、1五銀打、2五玉、3四角で―――(次の図)
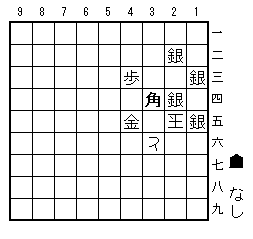 詰め上がり図
詰め上がり図
これで詰んだ。
「角角銀銀銀銀」の6枚の持駒のうち、5枚をペタペタと貼っていくような詰将棋となったが、それがこれをつくった意図である。「並べ詰め風の詰将棋をつくろう」と考えて、この詰将棋ができ上った。
詰将棋問題ばかり解いていると、捨て駒を考えるのがクセになる。逆に言えば、「並べ詰め」の訓練ができていないということになる。実戦で「並べ詰め」が現れたとき、難しくないのに妙に解きにくいのは、実戦のための練習問題としての詰将棋問題に「並べ詰め」のテイストが少ないからではないだろうか。
――――そんなことを前から思っていたので、「並べ詰め風の詰将棋をつくろう」と思ったのである。
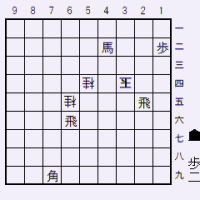
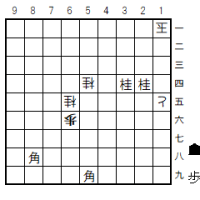
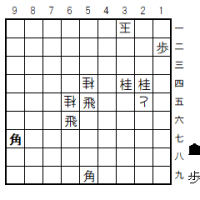
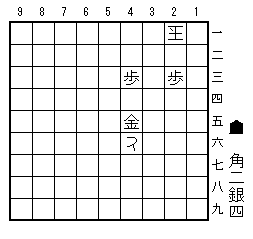 問題図
問題図
さて、もう一度「問題図」に戻って、ここからの2つの「紛れ筋」を解説する。
「紛れ筋」というのは「詰みそうだけど、でも、詰まない」という筋のことで、これが詰んでしまうと「余詰め」となってしまうので詰将棋の作者にとっては大事件となる。
「紛れ筋A=初手3二銀」と「紛れ筋B=初手3二角」について、解説する。
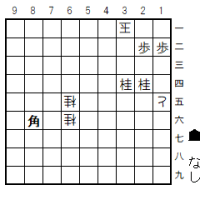
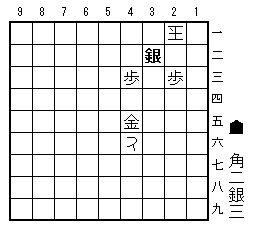 紛れ図A1
紛れ図A1
まず、「紛れ筋A=初手3二銀」(図)
これを同玉は、3三銀と打って詰む。3三同玉なら3四銀以下。
よって3三銀には4三玉と逃げるが、それでも5四角、5三玉、7五角以下、手数は長くなるが、詰んでしまうのだ。
ということで、「3二銀以下余詰めがある」と思っていたので、最初の案では「攻め方3二歩」を盤上に配置した問題図だったのだが、よく調べると、「3二銀には1二玉とかわして詰まない」と判明したのだった。1二玉に、2二歩成があるので、簡単にこの玉は詰んでしまうと初めは即断していたのだったが―――(次の図)
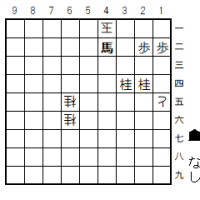
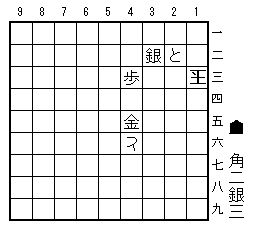 紛れ図A2
紛れ図A2
2二歩成に1三玉(図)と逃げて、この玉はどうやら詰みを逃れている。「角角銀銀銀」と持っていても、捕まらないのだ。
「紛れ筋A=初手3二銀」は、1二玉で逃れ―――が結論となる。
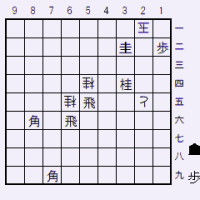
 紛れ図B
紛れ図B
次に、「紛れ筋B=初手3二角」(図)
角の場合は、1二玉と逃げると、2二歩成で確実に詰む。
なのでこれは3二同玉と応じるしかない。以下3三銀、4三玉と進むが、そこで攻め方の持駒は「角銀銀銀」。どうやらこの持駒ではこの玉は捕まらない。
ということで、「紛れ筋B=初手3二角」は、同玉と取って詰まない。
いまは「詰将棋ソフト」があるので、こうした「紛れ筋」を検討するのも楽ちんです。昔は大変だったことでしょうね。
答え: 2二銀 1二玉 1三銀打 2三玉 2四銀打 1四玉
3六角 同と 1五銀打 2六玉 3四角 まで11手詰め
解説:
初手正解手は2二銀。
代えて初手3二銀が紛れ筋。初手3二角もあり、これらの紛れ筋の解説については、最後に示すこととする。
 途中図1(初手2二銀まで)
途中図1(初手2二銀まで)初手2二銀(図)に、3二玉と逃げる手には、3三銀成がある。3三同玉、3四銀、2四玉、3三角以下、11手駒余り詰めとなる。
2手目は、1二玉が正解手となる(次の図)
 途中図2(2手目1二玉まで)
途中図2(2手目1二玉まで)ここで1三銀打の“平凡手”が3手目の正解手だが、他の手を考えるとすれば2一角がある。しかしそれは2三玉、3四銀(角)、1四玉となって、この玉は捕まらない。
この「途中図2」から、1三銀打、2三玉とすすめて、次の図になる。
 途中図3(4手目2三玉まで)
途中図3(4手目2三玉まで)ここで2四銀打と、3四銀、あるいは3四角がある。
しかし「3四」に銀や角を打つ手は、1四玉と応じられてみると、玉を逃がしてしまっている。1五~2六という脱出路を止めることができない。
2四銀打と、ここも“平凡手”にみえるこの手が正解となる。
以下1四玉に、そこで、3六角の好手がある(次の図)
 途中図4(7手目3六角まで)
途中図4(7手目3六角まで)3六角(図)。この手があるので、この玉を補足することができる。同とと取らせて、「3六」への脱出路を塞ぐ。
3六同とに、1五銀打、2五玉、3四角で―――(次の図)
 詰め上がり図
詰め上がり図これで詰んだ。
「角角銀銀銀銀」の6枚の持駒のうち、5枚をペタペタと貼っていくような詰将棋となったが、それがこれをつくった意図である。「並べ詰め風の詰将棋をつくろう」と考えて、この詰将棋ができ上った。
詰将棋問題ばかり解いていると、捨て駒を考えるのがクセになる。逆に言えば、「並べ詰め」の訓練ができていないということになる。実戦で「並べ詰め」が現れたとき、難しくないのに妙に解きにくいのは、実戦のための練習問題としての詰将棋問題に「並べ詰め」のテイストが少ないからではないだろうか。
――――そんなことを前から思っていたので、「並べ詰め風の詰将棋をつくろう」と思ったのである。
 問題図
問題図さて、もう一度「問題図」に戻って、ここからの2つの「紛れ筋」を解説する。
「紛れ筋」というのは「詰みそうだけど、でも、詰まない」という筋のことで、これが詰んでしまうと「余詰め」となってしまうので詰将棋の作者にとっては大事件となる。
「紛れ筋A=初手3二銀」と「紛れ筋B=初手3二角」について、解説する。
 紛れ図A1
紛れ図A1まず、「紛れ筋A=初手3二銀」(図)
これを同玉は、3三銀と打って詰む。3三同玉なら3四銀以下。
よって3三銀には4三玉と逃げるが、それでも5四角、5三玉、7五角以下、手数は長くなるが、詰んでしまうのだ。
ということで、「3二銀以下余詰めがある」と思っていたので、最初の案では「攻め方3二歩」を盤上に配置した問題図だったのだが、よく調べると、「3二銀には1二玉とかわして詰まない」と判明したのだった。1二玉に、2二歩成があるので、簡単にこの玉は詰んでしまうと初めは即断していたのだったが―――(次の図)
 紛れ図A2
紛れ図A22二歩成に1三玉(図)と逃げて、この玉はどうやら詰みを逃れている。「角角銀銀銀」と持っていても、捕まらないのだ。
「紛れ筋A=初手3二銀」は、1二玉で逃れ―――が結論となる。
 紛れ図B
紛れ図B次に、「紛れ筋B=初手3二角」(図)
角の場合は、1二玉と逃げると、2二歩成で確実に詰む。
なのでこれは3二同玉と応じるしかない。以下3三銀、4三玉と進むが、そこで攻め方の持駒は「角銀銀銀」。どうやらこの持駒ではこの玉は捕まらない。
ということで、「紛れ筋B=初手3二角」は、同玉と取って詰まない。
いまは「詰将棋ソフト」があるので、こうした「紛れ筋」を検討するのも楽ちんです。昔は大変だったことでしょうね。
















※コメント投稿者のブログIDはブログ作成者のみに通知されます