1:アルゴリズムによる高速化と計算機による高速化が明確に分離(区別)することが出来なくなった. つまり最新のアルゴリズムでは最新の計算機アーキテクチャでの実行を前提としたものが増えてきている.
2:計算量による理論的解析の優劣とソフトウェア実装後に計算機で実行したときの計算結果が大きく異なるという現象が見られる.その理由としては以下のような原因が考えられる
○理論的な解析時に想定されている最悪な場合という現象が計算機上で扱うことのできる問題の範囲では起こらない. 例えば,現在の計算機においては整数型の変数は大きくても 2^{64}-1 であるので,計算機で扱うことができる範囲では log_2 n 関数は大きくても 64 程度である(つまり定数とみなすこともできる).
○計算量の評価において,演算量とデータ移動量が混同されている(一般的には後者の方がコストが高い).
最近では計算機内部が以下のようなメモリ階層構造を持っている.

このメモリ階層構造では, 上位レベルになるほどアクセス速度が高速で小容量な記憶領域を,下位レベルになるほどアクセス速度が低速で大容量な記憶領域を保持している. そのため最適化分野に限らずソフトウェアの高速化のためには, 演算量とデータ移動量の割合を考慮してデータを適切に配置し,レジスタと主記憶装置の中間に位置するキャッシュメモリを有効に利用することは非常に重要である.つまり CPU の性能を引き出すことができるアルゴリズムというのは,データ移動量に対し演算量がある程度大きいこと(つまり {演算量}{データ移動量}の比がある程度大きいこと)}という性質を持っている必要がある.
3:最適化ソフトウェアと最新の計算技術の密な融合によって,一部の最適化問題では驚くほど大規模な問題が高速に処理できるようになった
○混合整数計画問題(MIP) : Gurobi や CPLEX などの商用ソルバーが有名だが,研究機関においても SCIP や CBC などのソルバーの開発も行われている.前処理等によって問題を小規模に変換する技術が重要.
○巡回セールスマン問題(TSP) : 数万から10万点規模の大規模問題が扱われている
○半正定値計画問題(SDP) :
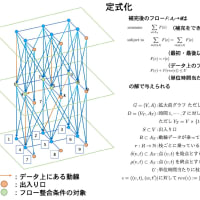
著者らのグループでは SDPARAや SDPA-GMP などのソフトウェアを用いて SDP に対する大規模,高速かつ安定計算を行っている.例えば京都大学 T2K スーパーコンピュータを用いて巨大な SDP に対してSDPARA によって最適解を求めることに成功し,世界最大規模の SDP を非常に正確に安定して解くことができた。今回の数値実験で解いた最も大きな SDP は下図のようなブロック対角構造を持っており、各行列の大きさは 19,460 x 19,460, 制約式の数は 36,795 個, 非零要素の総数は 6,731,930 個にも達する.

2:計算量による理論的解析の優劣とソフトウェア実装後に計算機で実行したときの計算結果が大きく異なるという現象が見られる.その理由としては以下のような原因が考えられる
○理論的な解析時に想定されている最悪な場合という現象が計算機上で扱うことのできる問題の範囲では起こらない. 例えば,現在の計算機においては整数型の変数は大きくても 2^{64}-1 であるので,計算機で扱うことができる範囲では log_2 n 関数は大きくても 64 程度である(つまり定数とみなすこともできる).
○計算量の評価において,演算量とデータ移動量が混同されている(一般的には後者の方がコストが高い).
最近では計算機内部が以下のようなメモリ階層構造を持っている.

このメモリ階層構造では, 上位レベルになるほどアクセス速度が高速で小容量な記憶領域を,下位レベルになるほどアクセス速度が低速で大容量な記憶領域を保持している. そのため最適化分野に限らずソフトウェアの高速化のためには, 演算量とデータ移動量の割合を考慮してデータを適切に配置し,レジスタと主記憶装置の中間に位置するキャッシュメモリを有効に利用することは非常に重要である.つまり CPU の性能を引き出すことができるアルゴリズムというのは,データ移動量に対し演算量がある程度大きいこと(つまり {演算量}{データ移動量}の比がある程度大きいこと)}という性質を持っている必要がある.
3:最適化ソフトウェアと最新の計算技術の密な融合によって,一部の最適化問題では驚くほど大規模な問題が高速に処理できるようになった
○混合整数計画問題(MIP) : Gurobi や CPLEX などの商用ソルバーが有名だが,研究機関においても SCIP や CBC などのソルバーの開発も行われている.前処理等によって問題を小規模に変換する技術が重要.
○巡回セールスマン問題(TSP) : 数万から10万点規模の大規模問題が扱われている
○半正定値計画問題(SDP) :
著者らのグループでは SDPARAや SDPA-GMP などのソフトウェアを用いて SDP に対する大規模,高速かつ安定計算を行っている.例えば京都大学 T2K スーパーコンピュータを用いて巨大な SDP に対してSDPARA によって最適解を求めることに成功し,世界最大規模の SDP を非常に正確に安定して解くことができた。今回の数値実験で解いた最も大きな SDP は下図のようなブロック対角構造を持っており、各行列の大きさは 19,460 x 19,460, 制約式の数は 36,795 個, 非零要素の総数は 6,731,930 個にも達する.