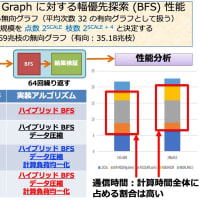
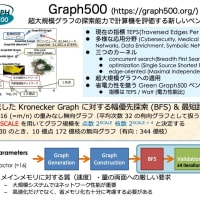
Lovász number の計算に関する続き。やはり GPU 計算クラスタでの計算は速い。mDIM が大きいので GPU 加速が効きやすい問題となっている。
今回用いたグラフデータ
http://mat.gsia.cmu.edu/COLOR03/INSTANCES/
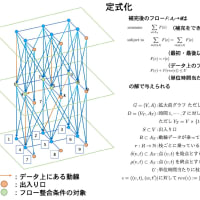
◯DSJC1000.9.col に対する SDP 緩和問題(Lovász number)
DSJC1000.9.col.dat-s
50052 = mDIM
1 = nBLOCK
1000 = bLOCKsTRUCT
◯計算サーバ1 : SandyBridge-EP 32 コアマシン
CPU Intel Xeon E5-4640 (8-core 2.40GHz 16MB cacheTDP:95w) x 4
Memory 512GB ACTICA製HPC専用メモリ DDR3 1600Mhz (16GB x 32枚) x 32
SDD Fusion IO 1.2TB SSD Card 1.2TB x 1
SSD SATA SSD 600GB x 3
HDD Enterprize 3.5" 3TB SATA HDD 3TB x 1
OS : CentOS 6.5
SDPA start at [Fri Mar 7 10:25:19 2014]
param is ./param.sdpa
data is /home/fujisawa/src/makepro/DSJC1000.9.col.dat-s : sparse
out is out.DSJC1000.9.col
NumThreads is set as 40
Schur computation : DENSE
mu thetaP thetaD objP objD alphaP alphaD beta
0 1.0e+04 1.0e+00 1.0e+00 -0.00e+00 +1.00e+05 7.3e-01 3.6e-01 2.00e-01
1 6.9e+03 2.7e-01 6.4e-01 +1.10e+02 +2.59e+06 1.0e+00 6.2e-01 2.00e-01
2 4.1e+03 8.8e-18 2.5e-01 +1.92e+02 +6.52e+05 7.8e-01 7.8e-01 2.00e-01
3 1.2e+03 1.8e-17 5.4e-02 +2.37e+02 +7.06e+04 7.7e-01 7.7e-01 2.00e-01
4 3.7e+02 2.6e-17 1.2e-02 +3.03e+02 +7.56e+03 7.7e-01 7.7e-01 2.00e-01
5 1.1e+02 3.5e-17 2.9e-03 +3.91e+02 +7.74e+02 8.0e-01 8.0e-01 2.00e-01
6 3.0e+01 4.4e-17 5.9e-04 +5.13e+02 +7.85e+01 8.7e-01 8.7e-01 2.00e-01
7 5.6e+00 5.3e-17 7.4e-05 +6.75e+02 +9.94e+00 1.0e+00 1.0e+00 2.00e-01
8 7.7e-01 5.3e-17 3.6e-20 +7.77e+02 +3.09e+00 6.4e-01 3.4e+00 1.00e-01
9 2.9e-01 5.3e-17 6.9e-20 +3.39e+02 +4.86e+01 7.5e-01 1.4e+00 1.00e-01
10 7.6e-02 6.2e-17 1.7e-20 +1.63e+02 +8.77e+01 7.8e-01 7.9e-01 1.00e-01
11 2.2e-02 7.0e-17 6.7e-21 +1.31e+02 +1.09e+02 8.6e-01 8.4e-01 1.00e-01
12 5.3e-03 7.0e-17 2.2e-20 +1.24e+02 +1.19e+02 8.9e-01 9.0e-01 1.00e-01
13 1.0e-03 7.0e-17 1.1e-21 +1.23e+02 +1.22e+02 9.2e-01 9.3e-01 1.00e-01
14 1.7e-04 8.8e-17 2.4e-20 +1.23e+02 +1.23e+02 9.4e-01 9.4e-01 1.00e-01
15 2.7e-05 8.8e-17 1.8e-20 +1.23e+02 +1.23e+02 9.6e-01 9.4e-01 1.00e-01
16 4.2e-06 1.1e-16 4.9e-20 +1.23e+02 +1.23e+02 9.6e-01 9.4e-01 1.00e-01
17 6.4e-07 1.1e-16 2.2e-20 +1.23e+02 +1.23e+02 9.5e-01 9.3e-01 1.00e-01
18 1.0e-07 1.1e-16 9.0e-20 +1.23e+02 +1.23e+02 9.3e-01 9.3e-01 1.00e-01
19 1.6e-08 1.2e-16 3.1e-20 +1.23e+02 +1.23e+02 9.5e-01 9.5e-01 1.00e-01
20 2.4e-09 1.4e-16 4.0e-20 +1.23e+02 +1.23e+02 9.5e-01 9.5e-01 1.00e-01
phase.value = pdOPT
Iteration = 20
mu = +2.3807348708913131e-09
relative gap = +1.9407830071021108e-08
gap = +2.3807323970004290e-06
digits = +7.7120230190094956e+00
objValPrimal = +1.2266865545456602e+02
objValDual = +1.2266865307383362e+02
p.feas.error = +1.4210854715202004e-14
d.feas.error = +3.9968028886505635e-15
total time = 2950.125270
◯計算サーバ2:GPU 計算クラスタ
Intel Xeon + 4 GPU マシン(4台)
CPU:Xeon X5690(3.46GHz,6コア)×2
メモリ:192GB(16GB×12)
HDD:SATA500GB×2(システム、システムバックアップ)
NIC : GbE x 1 & Inifiniband(FDR) x 1
GPGPU:Tesla C2075(C2070)×4
OS:CentOS 6.3 for x86_64
SDPA start at [Fri Mar 7 10:26:47 2014]
param is ./param.sdpa
data is /home/fujisawa/data/DSJC1000.9.col.dat-s : sparse
out is out.DSJC1000.9.col
NumNodes is set as 16
NumThreads is set as 3
Schur computation : DENSE
mu thetaP thetaD objP objD alphaP alphaD beta
0 1.0e+04 1.0e+00 1.0e+00 -0.00e+00 +1.00e+05 7.3e-01 3.6e-01 2.00e-01
1 6.9e+03 2.7e-01 6.4e-01 +1.10e+02 +2.59e+06 1.0e+00 6.2e-01 2.00e-01
2 4.1e+03 8.8e-18 2.5e-01 +1.92e+02 +6.52e+05 7.8e-01 7.8e-01 2.00e-01
3 1.2e+03 1.8e-17 5.4e-02 +2.37e+02 +7.06e+04 7.7e-01 7.7e-01 2.00e-01
4 3.7e+02 2.6e-17 1.2e-02 +3.03e+02 +7.56e+03 7.7e-01 7.7e-01 2.00e-01
5 1.1e+02 3.5e-17 2.9e-03 +3.91e+02 +7.74e+02 8.0e-01 8.0e-01 2.00e-01
6 3.0e+01 5.6e-16 5.9e-04 +5.13e+02 +7.85e+01 8.7e-01 8.7e-01 2.00e-01
7 5.6e+00 1.1e-15 7.4e-05 +6.75e+02 +9.94e+00 1.0e+00 1.0e+00 2.00e-01
8 7.7e-01 1.1e-15 4.0e-20 +7.77e+02 +3.09e+00 6.4e-01 3.4e+00 1.00e-01
9 2.9e-01 1.1e-15 1.4e-19 +3.39e+02 +4.86e+01 7.5e-01 1.4e+00 1.00e-01
10 7.6e-02 1.1e-15 4.4e-21 +1.63e+02 +8.77e+01 7.8e-01 7.9e-01 1.00e-01
11 2.2e-02 1.1e-15 8.9e-21 +1.31e+02 +1.09e+02 8.6e-01 8.4e-01 1.00e-01
12 5.3e-03 1.1e-15 1.6e-20 +1.24e+02 +1.19e+02 8.9e-01 9.0e-01 1.00e-01
13 1.0e-03 1.1e-15 2.7e-20 +1.23e+02 +1.22e+02 9.2e-01 9.3e-01 1.00e-01
14 1.7e-04 1.1e-15 1.2e-20 +1.23e+02 +1.23e+02 9.4e-01 9.4e-01 1.00e-01
15 2.7e-05 1.1e-15 5.1e-20 +1.23e+02 +1.23e+02 9.6e-01 9.4e-01 1.00e-01
16 4.2e-06 1.1e-15 7.4e-22 +1.23e+02 +1.23e+02 9.6e-01 9.4e-01 1.00e-01
17 6.4e-07 1.1e-15 2.2e-21 +1.23e+02 +1.23e+02 9.5e-01 9.3e-01 1.00e-01
18 1.0e-07 1.1e-15 2.7e-20 +1.23e+02 +1.23e+02 9.3e-01 9.3e-01 1.00e-01
19 1.6e-08 1.1e-15 1.8e-20 +1.23e+02 +1.23e+02 9.5e-01 9.5e-01 1.00e-01
20 2.4e-09 1.1e-15 1.4e-19 +1.23e+02 +1.23e+02 9.8e-01 9.8e-01 1.00e-01
21 2.7e-10 1.1e-15 1.2e-19 +1.23e+02 +1.23e+02 9.8e-01 9.8e-01 1.00e-01
phase.value = pdOPT
Iteration = 21
mu = +2.7154975473786538e-10
relative gap = +2.2136155263879887e-09
gap = +2.7154123927175533e-07
digits = +8.6548978076975249e+00
objValPrimal = +1.2266865511888591e+02
objValDual = +1.2266865484734467e+02
p.feas.error = +1.1368683772161603e-13
d.feas.error = +1.1990408665951691e-14
total time = 996.540333
今回用いたグラフデータ
http://mat.gsia.cmu.edu/COLOR03/INSTANCES/
◯DSJC1000.9.col に対する SDP 緩和問題(Lovász number)
DSJC1000.9.col.dat-s
50052 = mDIM
1 = nBLOCK
1000 = bLOCKsTRUCT
◯計算サーバ1 : SandyBridge-EP 32 コアマシン
CPU Intel Xeon E5-4640 (8-core 2.40GHz 16MB cacheTDP:95w) x 4
Memory 512GB ACTICA製HPC専用メモリ DDR3 1600Mhz (16GB x 32枚) x 32
SDD Fusion IO 1.2TB SSD Card 1.2TB x 1
SSD SATA SSD 600GB x 3
HDD Enterprize 3.5" 3TB SATA HDD 3TB x 1
OS : CentOS 6.5
SDPA start at [Fri Mar 7 10:25:19 2014]
param is ./param.sdpa
data is /home/fujisawa/src/makepro/DSJC1000.9.col.dat-s : sparse
out is out.DSJC1000.9.col
NumThreads is set as 40
Schur computation : DENSE
mu thetaP thetaD objP objD alphaP alphaD beta
0 1.0e+04 1.0e+00 1.0e+00 -0.00e+00 +1.00e+05 7.3e-01 3.6e-01 2.00e-01
1 6.9e+03 2.7e-01 6.4e-01 +1.10e+02 +2.59e+06 1.0e+00 6.2e-01 2.00e-01
2 4.1e+03 8.8e-18 2.5e-01 +1.92e+02 +6.52e+05 7.8e-01 7.8e-01 2.00e-01
3 1.2e+03 1.8e-17 5.4e-02 +2.37e+02 +7.06e+04 7.7e-01 7.7e-01 2.00e-01
4 3.7e+02 2.6e-17 1.2e-02 +3.03e+02 +7.56e+03 7.7e-01 7.7e-01 2.00e-01
5 1.1e+02 3.5e-17 2.9e-03 +3.91e+02 +7.74e+02 8.0e-01 8.0e-01 2.00e-01
6 3.0e+01 4.4e-17 5.9e-04 +5.13e+02 +7.85e+01 8.7e-01 8.7e-01 2.00e-01
7 5.6e+00 5.3e-17 7.4e-05 +6.75e+02 +9.94e+00 1.0e+00 1.0e+00 2.00e-01
8 7.7e-01 5.3e-17 3.6e-20 +7.77e+02 +3.09e+00 6.4e-01 3.4e+00 1.00e-01
9 2.9e-01 5.3e-17 6.9e-20 +3.39e+02 +4.86e+01 7.5e-01 1.4e+00 1.00e-01
10 7.6e-02 6.2e-17 1.7e-20 +1.63e+02 +8.77e+01 7.8e-01 7.9e-01 1.00e-01
11 2.2e-02 7.0e-17 6.7e-21 +1.31e+02 +1.09e+02 8.6e-01 8.4e-01 1.00e-01
12 5.3e-03 7.0e-17 2.2e-20 +1.24e+02 +1.19e+02 8.9e-01 9.0e-01 1.00e-01
13 1.0e-03 7.0e-17 1.1e-21 +1.23e+02 +1.22e+02 9.2e-01 9.3e-01 1.00e-01
14 1.7e-04 8.8e-17 2.4e-20 +1.23e+02 +1.23e+02 9.4e-01 9.4e-01 1.00e-01
15 2.7e-05 8.8e-17 1.8e-20 +1.23e+02 +1.23e+02 9.6e-01 9.4e-01 1.00e-01
16 4.2e-06 1.1e-16 4.9e-20 +1.23e+02 +1.23e+02 9.6e-01 9.4e-01 1.00e-01
17 6.4e-07 1.1e-16 2.2e-20 +1.23e+02 +1.23e+02 9.5e-01 9.3e-01 1.00e-01
18 1.0e-07 1.1e-16 9.0e-20 +1.23e+02 +1.23e+02 9.3e-01 9.3e-01 1.00e-01
19 1.6e-08 1.2e-16 3.1e-20 +1.23e+02 +1.23e+02 9.5e-01 9.5e-01 1.00e-01
20 2.4e-09 1.4e-16 4.0e-20 +1.23e+02 +1.23e+02 9.5e-01 9.5e-01 1.00e-01
phase.value = pdOPT
Iteration = 20
mu = +2.3807348708913131e-09
relative gap = +1.9407830071021108e-08
gap = +2.3807323970004290e-06
digits = +7.7120230190094956e+00
objValPrimal = +1.2266865545456602e+02
objValDual = +1.2266865307383362e+02
p.feas.error = +1.4210854715202004e-14
d.feas.error = +3.9968028886505635e-15
total time = 2950.125270
◯計算サーバ2:GPU 計算クラスタ
Intel Xeon + 4 GPU マシン(4台)
CPU:Xeon X5690(3.46GHz,6コア)×2
メモリ:192GB(16GB×12)
HDD:SATA500GB×2(システム、システムバックアップ)
NIC : GbE x 1 & Inifiniband(FDR) x 1
GPGPU:Tesla C2075(C2070)×4
OS:CentOS 6.3 for x86_64
SDPA start at [Fri Mar 7 10:26:47 2014]
param is ./param.sdpa
data is /home/fujisawa/data/DSJC1000.9.col.dat-s : sparse
out is out.DSJC1000.9.col
NumNodes is set as 16
NumThreads is set as 3
Schur computation : DENSE
mu thetaP thetaD objP objD alphaP alphaD beta
0 1.0e+04 1.0e+00 1.0e+00 -0.00e+00 +1.00e+05 7.3e-01 3.6e-01 2.00e-01
1 6.9e+03 2.7e-01 6.4e-01 +1.10e+02 +2.59e+06 1.0e+00 6.2e-01 2.00e-01
2 4.1e+03 8.8e-18 2.5e-01 +1.92e+02 +6.52e+05 7.8e-01 7.8e-01 2.00e-01
3 1.2e+03 1.8e-17 5.4e-02 +2.37e+02 +7.06e+04 7.7e-01 7.7e-01 2.00e-01
4 3.7e+02 2.6e-17 1.2e-02 +3.03e+02 +7.56e+03 7.7e-01 7.7e-01 2.00e-01
5 1.1e+02 3.5e-17 2.9e-03 +3.91e+02 +7.74e+02 8.0e-01 8.0e-01 2.00e-01
6 3.0e+01 5.6e-16 5.9e-04 +5.13e+02 +7.85e+01 8.7e-01 8.7e-01 2.00e-01
7 5.6e+00 1.1e-15 7.4e-05 +6.75e+02 +9.94e+00 1.0e+00 1.0e+00 2.00e-01
8 7.7e-01 1.1e-15 4.0e-20 +7.77e+02 +3.09e+00 6.4e-01 3.4e+00 1.00e-01
9 2.9e-01 1.1e-15 1.4e-19 +3.39e+02 +4.86e+01 7.5e-01 1.4e+00 1.00e-01
10 7.6e-02 1.1e-15 4.4e-21 +1.63e+02 +8.77e+01 7.8e-01 7.9e-01 1.00e-01
11 2.2e-02 1.1e-15 8.9e-21 +1.31e+02 +1.09e+02 8.6e-01 8.4e-01 1.00e-01
12 5.3e-03 1.1e-15 1.6e-20 +1.24e+02 +1.19e+02 8.9e-01 9.0e-01 1.00e-01
13 1.0e-03 1.1e-15 2.7e-20 +1.23e+02 +1.22e+02 9.2e-01 9.3e-01 1.00e-01
14 1.7e-04 1.1e-15 1.2e-20 +1.23e+02 +1.23e+02 9.4e-01 9.4e-01 1.00e-01
15 2.7e-05 1.1e-15 5.1e-20 +1.23e+02 +1.23e+02 9.6e-01 9.4e-01 1.00e-01
16 4.2e-06 1.1e-15 7.4e-22 +1.23e+02 +1.23e+02 9.6e-01 9.4e-01 1.00e-01
17 6.4e-07 1.1e-15 2.2e-21 +1.23e+02 +1.23e+02 9.5e-01 9.3e-01 1.00e-01
18 1.0e-07 1.1e-15 2.7e-20 +1.23e+02 +1.23e+02 9.3e-01 9.3e-01 1.00e-01
19 1.6e-08 1.1e-15 1.8e-20 +1.23e+02 +1.23e+02 9.5e-01 9.5e-01 1.00e-01
20 2.4e-09 1.1e-15 1.4e-19 +1.23e+02 +1.23e+02 9.8e-01 9.8e-01 1.00e-01
21 2.7e-10 1.1e-15 1.2e-19 +1.23e+02 +1.23e+02 9.8e-01 9.8e-01 1.00e-01
phase.value = pdOPT
Iteration = 21
mu = +2.7154975473786538e-10
relative gap = +2.2136155263879887e-09
gap = +2.7154123927175533e-07
digits = +8.6548978076975249e+00
objValPrimal = +1.2266865511888591e+02
objValDual = +1.2266865484734467e+02
p.feas.error = +1.1368683772161603e-13
d.feas.error = +1.1990408665951691e-14
total time = 996.540333