
4年生の算数は、来週から「およその数」に入ります。
講師の先生と、単元に入る前に教材研究をしました。この中で、一万までの概数の 「まで」 が話題になりました。私は、この「まで」を、もっと大きな位から一万の位までと上からその位までの意味で使いました。しかし、彼はそれに納得しません。
いろいろと説明するのですが、うまく説得できません。
そこで、考えてみました。
国語的に考えると「まで」は「から」と合わせて使われる概念だと思います。
つまり、「出発点から~...」「...到着点まで。」と範囲を表します。
この場合、到着点は、一万の位です。
では、出発点は「上の位から」なのか
「下の位(一の位)」なのかです。
まず、概数とは何かを考えます。
これは、「2つの数のどちらにより近いか」という考え方だと思います。
実際の問題で考えます。
例に出した問題の数字は
「54836」です。
この数を一万の位までの概数にするときはこう考えます。
50000 ←54836 60000
5万と6万の間にある、「54836」は、5万に近いので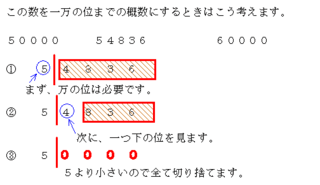
およそ5万と概数にします。(千の位の4を切り捨てる)
次に、この数を千の位までの概数にするときはこう考えます。
54000 54836→ 55000
5万4千と、5万5千の間にある、「54836」は、5万5千に近いので

およそ5万5千と概数にします。(百の位の8を切り上げる)
次に、この数を百の位までの概数にするときはこう考えます。
54800 ←54836 54900
5万4千8百と、5万4千9百の間にある、「54836」は、5万4千8百に近いので
およそ5万4千8百と概数にします。(十の位の3を切り捨てる)
次に、この数を十の位までの概数にするときはこう考えます。
54830 54836→ 54840
54830と、54840の間にある、「54836」は、54840に近いので
およそ54840と概数にします。(1の位の6を切り上げる)
こうして見てくると、「○の位までの概数」の意味が見えてきます。
並べてみると、万の位まで、千の位まで、百の位まで、十の位までとなるにしたがって、上の位(大きな位)からその位までを注目している様子が分かります。
やはり、「上の位から○の位までの概数」の前半部分が消えているのです。
ところで、このことについてネットで「goo相談室」で聞いてみました。
http://oshiete1.goo.ne.jp/qa4943584.html
やはり、「上の位から」という意見ばかりでした。
説得力のあったのは、例えば√2=1.4142..を小数第2位までの概数にする場合を考えると、下の位からが成り立たないことがわかります。という意見でした。
たしかに、円周率など小数点以下で概数にする場合、下の位からと考えると、下の位は無限に続くので意味が無くなります。
「から」にこだわって、少し勉強できたことが嬉しかったです。





















※コメント投稿者のブログIDはブログ作成者のみに通知されます