整数計画問題の解き方、扱い方

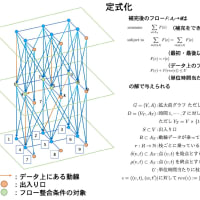
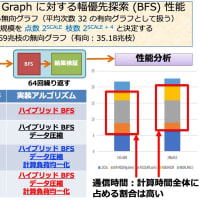
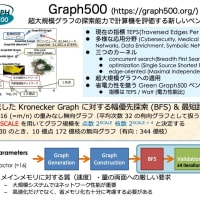
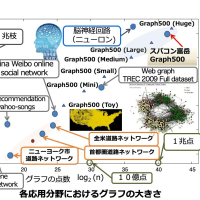
突然だが、整数計画問題に対する解き方、扱い方について。

１：整数計画ソルバー：
整数計画問題に対しては CPLEX, Gurobi 等の有償整数計画ソルバーが有名であり、世界中で広く使用されている。他にも NUOPT や MATLAB の
Optimization Toolboxなどの有償整数計画ソルバーが使用されている。また無償のソルバーでは GLPK や LP_SOLVE なども存在する.
現在では相当規模が大きな問題でも CPLEX などで最適に解くことができるようになっている.まずは整数計画ソルバーを試して解けない場合には以下の方法を試すという方針もある. ナップサック問題や施設配置問題などは結構大きな規模まで解くことができるだろう.

２：分枝限定法や分枝カット法：
整数計画ソルバーも分枝限定法や分枝カット法を採用しているが,多くの場合では一般の整数計画問題を想定している.よって手間はかかるが個別の問題に対して分枝限定法や分枝カット法を設計して実装した方がより大きな効果を期待できる. 巡回セールスマン問題(分枝カット法)や二次割当問題(分枝限定法)がこれに当てはまる.

３：メタヒューリスティックスなどの近似解法 :
メタヒューリスティックスは組合せ最適化問題に対する汎用的な解法として知られている.整数計画ソルバーでは扱えないような巨大な整数計画問題を解いたり,あるいは短時間にある程度良い解が欲しい場合には近似解法が適用されることが多い.メタ解法は近傍探索法の拡張であるが,整数変数の値の取り方について様々な方法が考案されている. 制約充足問題にタブー探索法などのメタ解法が適用されている.

４：その他の近似解法(列生成法などや容量スケーリング法など) :
列生成法は元問題の列の部分集合からなる部分問題をLP緩和問題として解いて,双対問題から得られる情報によって新たな列を生成する反復解法であり,集合分割問題や集合被覆問題などで利用されている. またロットサイズ決定問題のように整数変数が実数変数の上限を規定しているときは容量スケーリング法という反復解法を使用することができる.
列生成法の概略は以下の通りである.
A: 全変数の中から一部の変数(列)を選び出す.その変数のみを用いてLP緩和問題を解く
B: LP緩和問題の最適解の双対変数の情報から考慮していない残りの変数の 被約費用(reduced cost)を計算する. 被約費用が正の変数(列)を部分問題に追加して(最大化問題の場合),LP緩和問題を解く.このとき変数を一つずつ加える場合と複数同時に加える方法がある.
C: LP緩和問題の最適解が収束するまで列を追加していく.

５：上記の手法の複合(ハイブリッド型) :
元問題は大きすぎて整数計画ソルバーで解けない場合でも分割して部分問題にした場合には整数計画ソルバーで最適解が得られることもある.また上記の容量スケーリング法で得られた実行可能解をメタヒューリスティックスなどを用いてさらに改善する方法も考案されている.