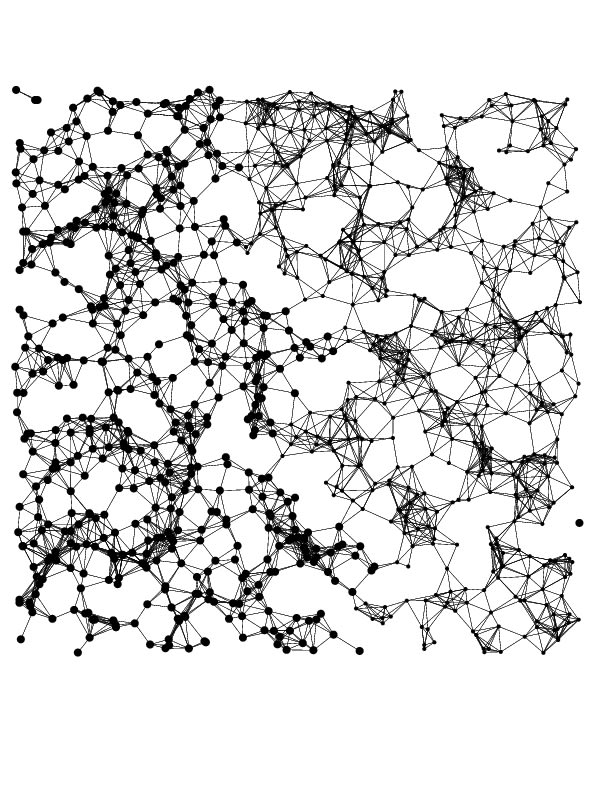
応用に役立つ50の最適化問題の 5.4 章(グラフ分割問題に対する SDP 緩和問題)において SDP 緩和問題を SDPA-GMP を用いて解いているが、SDPA ではダメなのか?という質問があった。この問題では SDPA を用いても別に問題は無いと思われるが、以下のように数値精度という点で SDPA-GMP に劣るので、出来れば SDPA-GMP の値の方を使いたい。
SDPA では主問題の最適目的関数値(上界) -1.1972046804133166e-01 > 双対問題の最適目的関数値(下界) -1.2187341887583791e-01 であるが、双対問題の実行可能性の指標(d.feas.error) があまり良くないので、SDPA-GMP の最適目的関数値 -1.1957989287e-01 が SDPA のこの上界と下界の範囲に含まれていない。この点がやはり気になったので、SDPA-GMP の方を用いた。
SDPA 7.3.1
objValPrimal = -1.1972046804133166e-01 <-- 主問題の目的関数値
objValDual = -1.2187341887583791e-01 <-- 双対問題の目的関数値
p.feas.error = +2.2737367544323206e-13
d.feas.error = +2.1173717223987865e-09
SDPA-GMP 7.1.2
objValPrimal = -1.1957989287e-01 <-- 主問題の目的関数値
objValDual = -1.1957989287e-01 <-- 双対問題の目的関数値
p.feas.error = 2.8917634547e-76
d.feas.error = 4.5890565996e-38
SDPA では主問題の最適目的関数値(上界) -1.1972046804133166e-01 > 双対問題の最適目的関数値(下界) -1.2187341887583791e-01 であるが、双対問題の実行可能性の指標(d.feas.error) があまり良くないので、SDPA-GMP の最適目的関数値 -1.1957989287e-01 が SDPA のこの上界と下界の範囲に含まれていない。この点がやはり気になったので、SDPA-GMP の方を用いた。
SDPA 7.3.1
objValPrimal = -1.1972046804133166e-01 <-- 主問題の目的関数値
objValDual = -1.2187341887583791e-01 <-- 双対問題の目的関数値
p.feas.error = +2.2737367544323206e-13
d.feas.error = +2.1173717223987865e-09
SDPA-GMP 7.1.2
objValPrimal = -1.1957989287e-01 <-- 主問題の目的関数値
objValDual = -1.1957989287e-01 <-- 双対問題の目的関数値
p.feas.error = 2.8917634547e-76
d.feas.error = 4.5890565996e-38





















遅れない(?)です。仕事遅くなりまして
すいませんが、帰国までお待ちください。
送りました。
どこに送っていただいたのでしょうか?