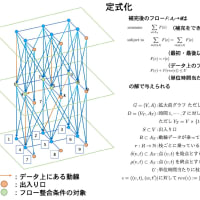
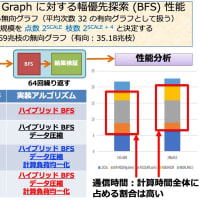
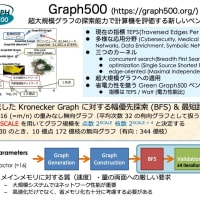
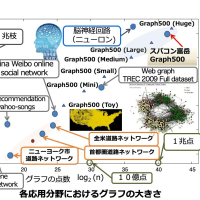
Title:
Peta-scale General Solver for Semidefinite Programming Problems with over Two Million Constraints
Abstract:
The semidefinite programming (SDP) problem is one of the most central problems in mathematical optimization. The primal-dual interior-point method (PDIPM) is one of
the most powerful algorithms for solving SDP problems, and many research groups have employed it for developing software packages. However, two well-known major bottleneck parts i.e., the generation of the Schur complement matrix (SCM) and its Cholesky factorization, exist in the algorithmic framework of PDIPM.
We have developed a new version of SDPARA, which is a parallel implementation on multiples CPUs and GPUs for solving extremely large-scale SDP problems with over a million constraints. SDPARA can automatically extract the unique characteristics from an SDP problem and identify the bottleneck. When the generation of SCM becomes a
bottleneck part, SDPARA can attain high scalability using a large quantity of CPU cores and some techniques of processor affinity and memory interleaving. SDPARA can also perform parallel Cholesky factorization using thousands of GPUs and techniques to overlap computation and communication if an SDP problem has over two million constraints and Cholesky factorization constitutes a bottleneck part.We demonstrate that SDPARA is a high-performance general solver for SDPs in various application fields through numerical experiments at the TSUBAME 2.5 supercomputer, and we solved the largest SDP problem (which has over 2.33 million constraints), thereby creating a new world record. Our implementation also achieved 1.713 PFlops in double precision for large-scale Cholesky factorization using 2,720 CPUs and 4,080 GPUs.
Peta-scale General Solver for Semidefinite Programming Problems with over Two Million Constraints
Abstract:
The semidefinite programming (SDP) problem is one of the most central problems in mathematical optimization. The primal-dual interior-point method (PDIPM) is one of
the most powerful algorithms for solving SDP problems, and many research groups have employed it for developing software packages. However, two well-known major bottleneck parts i.e., the generation of the Schur complement matrix (SCM) and its Cholesky factorization, exist in the algorithmic framework of PDIPM.
We have developed a new version of SDPARA, which is a parallel implementation on multiples CPUs and GPUs for solving extremely large-scale SDP problems with over a million constraints. SDPARA can automatically extract the unique characteristics from an SDP problem and identify the bottleneck. When the generation of SCM becomes a
bottleneck part, SDPARA can attain high scalability using a large quantity of CPU cores and some techniques of processor affinity and memory interleaving. SDPARA can also perform parallel Cholesky factorization using thousands of GPUs and techniques to overlap computation and communication if an SDP problem has over two million constraints and Cholesky factorization constitutes a bottleneck part.We demonstrate that SDPARA is a high-performance general solver for SDPs in various application fields through numerical experiments at the TSUBAME 2.5 supercomputer, and we solved the largest SDP problem (which has over 2.33 million constraints), thereby creating a new world record. Our implementation also achieved 1.713 PFlops in double precision for large-scale Cholesky factorization using 2,720 CPUs and 4,080 GPUs.