算数の宿題の続きです。
jack fujiiさんから相似を使わない解法がある、と言われ、さらに悩んでしまいました。
そこで、小学生の算数、という前提だと「旅人算」的な解き方はどうでしょうか?
まずは図を反転させます
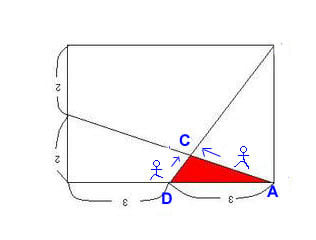
AさんとDさんが向かい合わせに歩く、と考えます。
横軸が時間、縦軸が道のりとすると、勾配は早さになります。
つまりAさんの速さは1/3(=2/6)で、Dさんの速さは4/3(Aさんの4倍)です。
出会いまでの総時間が3ですから、Dさんが要した時間は3/(1+4)=3/5となり
その間の道のり(=ADを底辺とした場合の高さ)は3/5*4/3=4/5です。
したがって△ACDの面積=3*4/5÷2=6/5
でもこれって、結局比と傾きを使ってるから、相似と同じですかね・・・
※あと、これって「旅人算」でいいのかしら?「仕事算」とかいうのもあったような・・・
jack fujiiさんから相似を使わない解法がある、と言われ、さらに悩んでしまいました。
そこで、小学生の算数、という前提だと「旅人算」的な解き方はどうでしょうか?
まずは図を反転させます

AさんとDさんが向かい合わせに歩く、と考えます。
横軸が時間、縦軸が道のりとすると、勾配は早さになります。
つまりAさんの速さは1/3(=2/6)で、Dさんの速さは4/3(Aさんの4倍)です。
出会いまでの総時間が3ですから、Dさんが要した時間は3/(1+4)=3/5となり
その間の道のり(=ADを底辺とした場合の高さ)は3/5*4/3=4/5です。
したがって△ACDの面積=3*4/5÷2=6/5
でもこれって、結局比と傾きを使ってるから、相似と同じですかね・・・

※あと、これって「旅人算」でいいのかしら?「仕事算」とかいうのもあったような・・・















