といっても下ネタではありません(笑)
先日紹介した『渋滞学』でへぇ、と思った話(数学に詳しい方には当たり前のことかもしれませんが)。
「パイこね変換」というのはカオス理論の用語。
これはパイ生地をこねるときの伸ばして折りたたんで、という操作のことで、これを繰り行うことで生地の中の含有物を最も効率よく混ぜることが出来るということがカオス理論で証明されているんだそうです。
その証明はそれですごいことだと思うのですが、本題は、この操作はコンピューターにはできないということ。
パイこねの操作を単純化します。
まず0から1までの範囲でX(パイ生地の中の成分の位置)を決める。
そしてこの0から1までをパイ生地とする。パイ生地は2倍に伸ばして折りたたむことを繰り返す。
そして
Xが0.5より小さければ2倍して2Xとする
(=伸ばしても1より小さい場所にあるので成分は折り返されずに2Xのところにあ移動しただけ)
Xが0.5より大きければ2-2Xとする
(=伸ばしたときに1より大きくなるので折りかえされてしまい、伸ばしたとき(全体で2)の向こう端からの距離分の場所に戻ってくる)
たとえば0.1を最初に選ぶと
1回目 0.2
2回目 0.4
3回目 0.8
4回目 0.4
5回目 0.8
以後0.4と0.8の繰り返しになります。
伸ばして折りたたむのですから、行ったりきたりになる、ということですね。
ところがコンピュータに計算させるとこのようになります(excelで実際にやってみたものです。左上から順番になってます。)
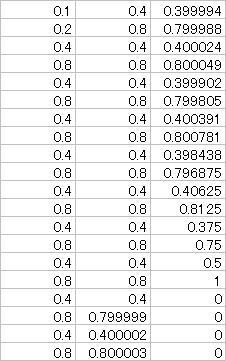
途中から数字がズレだして、最後は0になってしまいます。
これはコンピュータが10進数を2進数に変換して格納しているためで、本来10進数を2進数に変換すると一般に無限のケタが必要になりますが、コンピュータ内の数字の格納場所が有限なために一般に小さな誤差が生じてしまいます。
そしてパイこね変換はコンピュータにとってはとても意地悪な操作になっていて、2倍するなどという操作のたびにこの誤差も2倍に拡大し、これを繰り返すと目に見える誤差になってしまいます。
普段wordなどでマイクロソフトの差し出がましい設定にイラついたりしている身にはちょっとした意趣返しにもなりました(別にマイクロソフトに仕返しができたわけじゃないんですけどね(^^;)
本の中では、これは単なるトリビアではなく、現象を理解するのに微積分的な対象を連続の世界でとらえるアプローチと、デジタル的、離散的なアプローチがあって、それぞれはその対象とスケールによって有効性が違ってくる。
離散的なアプローチにはコンピューターは有効だがそれは離散量しか扱えない、という文脈で語られています。
そして、実は微積分の発明される400年以上前、物理現象を離散的に捉えていたときの手法が、微積分を使って計算してきたものをコンピュータを使って計算しようとする際の連続量を離散量に変換する手法として再び注目されてきたのだそうです。
昨日のエントリにもあるように上澄みだけを「クイズ王」として使わせていただいている身(正確にはとても「王」のレベルではないですが)としては、学問の歴史の厚みを改めて感じる話であります。
先日紹介した『渋滞学』でへぇ、と思った話(数学に詳しい方には当たり前のことかもしれませんが)。
「パイこね変換」というのはカオス理論の用語。
これはパイ生地をこねるときの伸ばして折りたたんで、という操作のことで、これを繰り行うことで生地の中の含有物を最も効率よく混ぜることが出来るということがカオス理論で証明されているんだそうです。
その証明はそれですごいことだと思うのですが、本題は、この操作はコンピューターにはできないということ。
パイこねの操作を単純化します。
まず0から1までの範囲でX(パイ生地の中の成分の位置)を決める。
そしてこの0から1までをパイ生地とする。パイ生地は2倍に伸ばして折りたたむことを繰り返す。
そして
Xが0.5より小さければ2倍して2Xとする
(=伸ばしても1より小さい場所にあるので成分は折り返されずに2Xのところにあ移動しただけ)
Xが0.5より大きければ2-2Xとする
(=伸ばしたときに1より大きくなるので折りかえされてしまい、伸ばしたとき(全体で2)の向こう端からの距離分の場所に戻ってくる)
たとえば0.1を最初に選ぶと
1回目 0.2
2回目 0.4
3回目 0.8
4回目 0.4
5回目 0.8
以後0.4と0.8の繰り返しになります。
伸ばして折りたたむのですから、行ったりきたりになる、ということですね。
ところがコンピュータに計算させるとこのようになります(excelで実際にやってみたものです。左上から順番になってます。)

途中から数字がズレだして、最後は0になってしまいます。
これはコンピュータが10進数を2進数に変換して格納しているためで、本来10進数を2進数に変換すると一般に無限のケタが必要になりますが、コンピュータ内の数字の格納場所が有限なために一般に小さな誤差が生じてしまいます。
そしてパイこね変換はコンピュータにとってはとても意地悪な操作になっていて、2倍するなどという操作のたびにこの誤差も2倍に拡大し、これを繰り返すと目に見える誤差になってしまいます。
普段wordなどでマイクロソフトの差し出がましい設定にイラついたりしている身にはちょっとした意趣返しにもなりました(別にマイクロソフトに仕返しができたわけじゃないんですけどね(^^;)
本の中では、これは単なるトリビアではなく、現象を理解するのに微積分的な対象を連続の世界でとらえるアプローチと、デジタル的、離散的なアプローチがあって、それぞれはその対象とスケールによって有効性が違ってくる。
離散的なアプローチにはコンピューターは有効だがそれは離散量しか扱えない、という文脈で語られています。
そして、実は微積分の発明される400年以上前、物理現象を離散的に捉えていたときの手法が、微積分を使って計算してきたものをコンピュータを使って計算しようとする際の連続量を離散量に変換する手法として再び注目されてきたのだそうです。
昨日のエントリにもあるように上澄みだけを「クイズ王」として使わせていただいている身(正確にはとても「王」のレベルではないですが)としては、学問の歴史の厚みを改めて感じる話であります。