ド・モアブルの公式(馴染みの文字はnだが、後で分枝するのでmを使う)
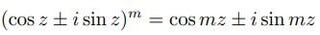
において、cos mz 、sin mzについて解くと、次のようになる。
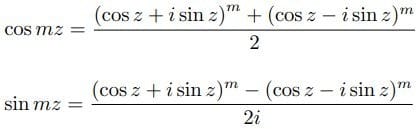 (1)
(1)
(1)で、mを無限大数nとおくと、
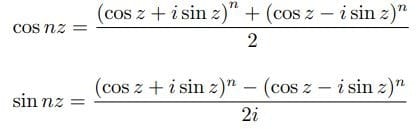
となる。オイラーはこの式を基礎に、「虚指数量が実の弧の正弦と余弦に帰着される様式」(オイラーの公式)を導いた。これはn倍角の公式といってよいだろう。
これに対して、「虚対数が円弧に帰着される様式」を導くときは、(1)式のmを無限小数、すなわちm=1/nとおいた次の式を基礎にしている。

こちらは1/n倍角の公式といってよいだろう。対数は指数の逆関数だから、自然な設定といえるだろう。
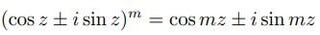
において、cos mz 、sin mzについて解くと、次のようになる。
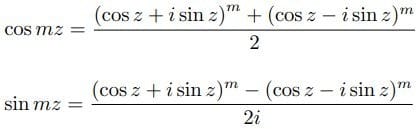 (1)
(1)(1)で、mを無限大数nとおくと、
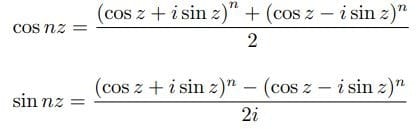
となる。オイラーはこの式を基礎に、「虚指数量が実の弧の正弦と余弦に帰着される様式」(オイラーの公式)を導いた。これはn倍角の公式といってよいだろう。
これに対して、「虚対数が円弧に帰着される様式」を導くときは、(1)式のmを無限小数、すなわちm=1/nとおいた次の式を基礎にしている。

こちらは1/n倍角の公式といってよいだろう。対数は指数の逆関数だから、自然な設定といえるだろう。









