1年ほど前、特殊相対性理論の形成過程と複合論(新しい弁証法の理論)は相性がいいのではないかと思い、参考になりそうな文献を読みはじめた。
読みすすめていくうちに、これまで挙げてきた複合論の例よりも、わかりやすく展開できるのではないかと思うようになった。アインシュタインを通して、これのまで議論を見直し、発展させてみようと思った。
双子のパラドックスは、相対性理論において、運動系の時計の遅れに関して提出されたパラドックスである。それはアインシュタインの時計のパラドックスを1911年にポール・ランジュバンが双子をモデルに仕立てたものだという。次のようなものである。
双子の兄弟がいる。兄は光速に近いロケットで宇宙旅行に出かけ再び地球にもどってくる。弟は地球にとどまっている。弟から見ると、兄が運動系にいるため、兄の時間が遅れているように見える。すなわち、兄が地球にもどったとき、兄の方が弟より若い。一方、運動が相対的であることを考えると、兄から見れば、弟の方が運動系にあるため、弟の時間が遅れているように見える。すなわち、双子が再会したとき、弟の方が兄より若い。弟から見るときと兄から見るときとでは、結果が逆になっている。
しかし、ここでタイトルとして提示する「双子のパラドックス」は、このような運動系における時計の遅れに関するものではない。わたしは、この「双子のパラドックス」ということばを借りて、弁証法の新しい理論を展開してみたいと思うのである。
弁証法は、現代ではヘーゲル・マルクス主義の考え方が主流である。しかし、歴史的に見ると、さまざまな立場があり、今日の主流の考え方は、たかだがこの150年ほどのもので、きわめて制約されたものだと思う。
わたしの試みは、「弁証法」の語源である「ディアレクティケー」の可能性を探究していると言えると思う。これまで展開してきた複合論を特殊相対性理論の形成過程を通して見直してみたいのである。
さて、わたしは「双子のパラドックス」に、運動系の時間の遅れではなく、違った内容を盛り込もうと考えている。それは、アインシュタインが1905年の論文で提示した2つの原理、すなわち、(特殊)相対性原理と光速度一定の原理のことである。
わたしはこの2つの原理を「双子」と見る。しかも、この「双子」は、ガリレオの相対性原理とマクスウェルの方程式のなかの光速度の一定性という別の「双子」によって「混成」された「双子」とみるのである。
「双子」は、わたしが提起している弁証法の新しい理論の核心にあるものである。
相対性原理と光速度一定の原理を、双子と呼ぶのは、わたしが初めてだと思う。しかし、2つの原理をパラドックスと呼ぶのは、わたしが初めてではない。2つの原理とパラドックスと関連させたのは、アインシュタイン本人である。『特殊および一般「相対性理論」について』(金子務訳)に、次のようにある。
さて、前述のバラドックスはこう表現できる。古典力学で使用される、一つの慣性系から他の慣性系へ移る場合の事象の空間座標と時間の結合規則に従えば、二つの仮定
一、光速度の不変性
二、法則(特に光速度不変の法則)は、慣性系の選び方とは無関係であること(特殊相対性原理)
は、(両方ともそれぞれ経験によって支持されているのにもかかわらず)たがいに両立しえないものなのだ、と。
「双子のパラドックス」ということばの指示する内容を、運動系の時間の遅れから、特殊相対性理論の核心である2つの原理へと変える。これを基礎に新しい弁証法の理論を展開したいと思う。
2008年に書いた相対性理論に関する記事を「双子のパラドックス――弁証法1905(Ⅰ)」として 、まとめた。
「表出論のゆくえ2008」 「1905年における光の粒子性と波動性について」(試論14)と重なっているが、「時間の同調の定義と偏微分方程式について 」が入っている。 また、これまで「熱力学か、電磁気学か」で割愛していた写真(「自伝ノート」に対する訂正)をいれている。
「双子のパラドックス――弁証法1905 」というタイトルは1年前に浮かんできたものである。このタイトルのもとで、相対性理論の形成過程の把握と弁証法の理論の見直しをやろうと思ってきた。今回はその第一声である。
「双子のパラドックス」ということばから「宇宙旅行」ではなく、「相対性原理と光速度一定の原理」が連想されるようになる。そして、それが「弁証法」と結びつく。そんな日が来ればいいなあと思う。わたしの夢である。
目次は、次のようになっている。
目次
はしがき
1 内的類似性の拡張
2 時間の同調の定義と偏微分方程式について
3 熱力学か、電磁気学か
4 相対性理論の形成と武谷三段階論
5 アインシュタインの思考モデルと2つの基準
6 2つの基準の包摂
7 表出のなかの悟性と理性
8 「論理的なもの」とアインシュタインの認識論
9 弁証法の場
10 1905年における光の粒子性と波動性について
11 表出論のゆくえ
1952年、マイケルソンの生誕100年を記念した会議に寄せられたアインシュタインの手紙には、次のように書かれているという。(G・ホルトンの「アインシュタイン・マイケルソン・〈決定的〉実験」『アインシュタイン研究』所収参照)
いうまでもなく、ひとつの理論の樹立に導く論理的な道というものはありません。事実の知識を注意ぶかく考慮しながら、手さぐりで組み立ててゆくだけです。
このアインシュタインの「率直な告白」(G・ホルトン)は、ヘルムホルツの「登山者」や湯川秀樹の「旅人」の精神と同じものだと思う。
複合論はアインシュタインの「手さぐり」と同調している。
複合論は、認識における対立の統一過程を複素数のかけ算をモデルにして表現している。それは次のようなものだ。
| 1(選択) | A =a+bi |
| A' =c+di | |
| 2(混成) | A×A' =(a+bi)×(c+di) |
| ≒(a+di)×(c+bi) | |
| 3(統一) | =(ac-bd)+(ab+cd)i |
| =x+yi | |
| =B |
これは、「論理的な道」ではなく、「手さぐりで組み立ててゆく」過程を表わしているのである。
G・ホルトンの「アインシュタイン・マイケルソン・〈決定的〉実験」(『アインシュタイン研究』所収参照)を読んでいた。その中に、シャンクランドのインタヴューに答えた次のようなアインシュタインのことばが引用されていた。
自分の問題と格闘し、解を見出すためにあらゆることを試み、そしてついに得られた解は、きわめて遠周りをしたやり方でもたらされることが多い。これが正しい描像である。
これは、アインシュタインが研究の心的過程をふりかえって述べたものである。湯川秀樹の「旅人」の精神と同じものだと思う。また、ヘルムホルツの「登山者」の精神と同じだと思う。
ヘルムホルツは、マックスウェルの電磁場理論を改作してドイツに導入した科学者で、弟子にはヘルツがいる。アインシュタインは1899年の手紙の中で、ヘルムホルツの本に言及して、「ヘルムホルツの考えの独創性と独自性をますます尊敬するようになった」と記している。(安孫子誠也『アインシュタイン相対性理論の誕生』参照)
ヘルムホルツの「登山者」。ハンス・セリエ『夢から発見へ』( 田多井 吉之介訳 1969年)のなかに引用されていたヘルムホルツのことばが強く印象に残っている。
アインシュタインがヘルムホルツから引き継いだものは、熱力学や電磁気学だけではない。なによりも研究の姿勢そのものだったと思う。
道を知らないで、苦しみながら上にゆっくり登り、もう歩けなくなって自分の足跡をもう一度たどらねばならない。だが、考えてみたら、幸運からか、ともかく新しい道筋を見つけ、またほんのちょっと進み、とうとう長くかかってたどりついたところ、正しい登山の知恵さえ心得ていたら、それを登ればよかったんだという広い道がそこにあるのを知って恥かしくなる。こんな山をさ迷っている人に自分をたとえてもらって、いっこう差し支えない。私の仕事について、読者には当然、自分の誤りについて何もいわなかった。そして、困難なしに高い頂上に登れる大きな道しか書きはしなかった。
安孫子誠也氏は「アインシュタイン相対性理論の誕生」のなかで、ローレンツとアインシュタインの相対性理論を区別するのは、光速度一定を原理として要請しているかどうかであると述べている。この見解は優れていると思い、踏襲するだけでよいと思っていた。しかし、いくつか文献を読み、自分なりに相対性理論が誕生していく過程を思い描いてみると、光速度一定の原理だけを強調するのは、一方的だと思えてきた。やはり、相対性原理と光速度一定原理の両方がローレンツとアインシュタインの違いなのではないかと思うようになった。
安孫子氏が強調するように、アインシュタインにあってローレンツにないものは、「運動学」であり、これがローレンツとアインシュタインの相対性理論の違いである。「運動学」とは、「物理現象を表現し記述するための数学的枠組み」である。そして、この「運動学」の前提になっているのは、光速度一定の原理と相対性原理である。2つが関連することによって、運動学が構成されている。ローレンツとアインシュタインを区別するのは、相対性と光速度一定の2つを原理として要請しているかどうかにあると思う。
安孫子氏が光速度一定の原理を強調することは、相対性理論がマクスウェル電磁場理論を前提としないという主張と結びついている。もちろん、広くいえば、相対性理論はマクスウェル理論を前提にしているのだが、安孫子氏が「前提」にしていないというのは、正確にいえば、マクスウェルの電磁場理論を、修正を必要としないそのまま引き継ぐ理論と考えないという意味である。直接には、輻射の説明に対してマクスウェルの理論は限界をもっていることを踏まえて、相対性理論は構築されていることを指している。
安孫子誠也氏の見解を確認しておこう。
「光速度の一定性」は、マクスウェル方程式に相対性原理を適用することによって得られる結論である。しかしながらアインシュタインは、「光速度不変の原理」を、マクスウェル方程式や相対性原理を前提とはしない、それ自体として独立した原理にまで高めて設定したのである。
しかしながら、ローレンツ変換を導くために、アインシュタインはマクスウェル方程式と相対性原理から導かれる「光速度の一定性」を必要とし、そこから彼はすでに時間概念の変革を導き出していた。したがって、マクスウェルの電磁場理論を超越するためには、彼はこの「光速度の一定性」を、「光速度不変の原理」の地位までに高めざるをえなかったのである。
かくして、ローレンツ―ポアンカレ理論とアインシュタイン理論との本質的な違いは、「光速度不変の原理」が独立の要請として樹立されていたかどうかだという結論に到達する。言い換えれば、ローレンツ―ポアンカレ理論は、特殊相対性理論にとって本質的な「運動学の部」を欠いていたのである。この「運動学の部」において、「相対性原理」と「光速度不変の原理」をもとにして、初めて正しい形のローレンツ変換が導出されたのだった(それまでは、誤りを含むローレンツ変換式が天下り的に仮定されていたのである)。
最後の引用文において、後半には異論がない。しかし、前半は、「相対性原理」が欠如しているのではないか、というのがわたしの見解である。いいかえれば、「言い換えれば」に飛躍があり、「言い換え」になっていないと思う。
安孫子氏の見解を一方的だと思うようになったのは、『特殊および一般「相対性理論」について』のなかで、アインシュタインが次のように述べていたからである。
相対性原理によれば、真空中の光の伝播法則は、すべての他の一般法則と同様に、列車を基準体としようが、レールを基準体としようが、同じことにならねばならない。ところが、われわれの考察によれば、それが不可能のように思える。すべての光線が堤防に関して速度cで伝播するとすれば、まさにそのことのために、列車を関する光の伝播法則はこれとは別のものにならなければならない――すなわち相対性原理と矛盾する。
このディレンマを考えてみれば、相対性原理か簡明な真空中の光の伝播法則かの、どちらかを放棄せざるをえないように思える。
これまでの論議に注意深くついてきた読者は、心底ではきっと、自然さかつ簡明さのゆえにほとんど拒み難く感じている相対性原理が支持されて、一方、真空中の光の伝播法則は、相対性原理と結びついた、より複雑な法則に置きかえられることを期待するだろう。しかし、理論物理学の進展から、この道を、辿れないことが示された。運動物体の電気力学的、光学的諸過程について道を拓いたH・A・ローレンツの理論的研究によると、この領域の経験では、電磁気学的な諸過程に関するある一つの理論が、抗い難い必然性をもって導かれるのであって、その理論からは、真空中の光速度が一定であるという法則が避くべからざる結論となるのである。このために、この相対性原理に矛盾するような経験的事実は、何一つ見いだせないにもかかわらず、指導的な理論家たちはむしろこの原理をなくしてしまう方向に傾いていた。
ここに相対性理論が登場した。時間と空間についての物理的な概念を分析することによって、現実的には相対性原理と光の伝播法則との間との不一致は、まったく存在しないこと、それどころか、この二つの法則を組織的に、しっかり把握することによって、論理的に異論の余地ない理論に到達することが示された。(金子務訳)
これを読んで、光速度一定の原理よりも、むしろ相対性原理の方が、アインシュタインの独自性ではないかという気になったのである。安孫子氏の表現を借りれば、アインシュタインは、「相対性」を、ガリレイの相対性原理や光速度の一定性を前提としない、それ自体として独立した原理にまで高めて設定した、といいたくなったのである。
もちろん、光速度一定の原理は、はずせない。とすれば、光速度一定の原理と相対性原理の両方を原理として要請するところに、アインシュタインの独自性をみるべきなのではないかと思うようになったのである。
安孫子氏から、アインシュタインの独自性の契機として、相対性原理が抜けたのは、おそらく、ポアンカレの「相対性原理」の過大評価があったのではないかと思われる。
もし、特殊相対性理論の主要な内容が、マイケルソンーモーレーの実験の説明とローレンツ変換の提出であったとするならば、それはすでに一九〇四年のローレンツ理論によって済まされていたと言える。また、もし相対性原理導入の重要性を強調するのならば、そのローレンツ理論への通用は一九〇五~一九〇六年のボアンカレ理論によって行われたと言えるのである。この論争は、しばしばローレンツーアインシュタイン問題と呼ばれており、いまだに完全に決着がついたとは言い難い。
安孫子氏が『アインシュタイン相対性理論の誕生』のなかで引用しているポアンカレの「科学と仮説」を読むと、確かに、アインシュタインの考えと同じではないかと思う。しかし、「ローレンツ‐ポアンカレの相対性理論」とアインシュタインの相対性理論は、違うのである。
広重徹氏が簡潔に指摘している(「相対論はどこから生まれたか」『アインシュタイン研究』所収)。
たしかに、それ(「ローレンツ変換」という名称が初めて使われた1905―6年のポアンカレの論文、ホイッテカーが「ポアンカレ‐ローレンツの相対性理論」とよんだもの――引用者注)は相対論とよびたくなるような理論であった。数式の面からみると、それは相対論と同じ形をしている。そのうえポアンカレは、しばしば「相対性原理」ということを唱えている。しかし見落としてならないのは、それで彼が意味したのは、対エーテル運動の効果の実験的検出不可能性のことだったということである。ポアンカレにとって、それは理論からの帰結として説明されるべきものであって、アインシュタインにおけるように、それの上に全理論が築かれる構成的原理ではなかった。ローレンツ‐ポアンカレの理論は、あくまで、生じているはずの効果が表に現われないことを説明する理論だったのである。この点が、それを、すべての慣性系の同等性という原理から出発する相対論から決定的に区別するのである。
さて、ローレンツは、マイケルソン―モーレーの実験の説明として、ローレンツ収縮と局所時間の考えを提出した。そして、このローレンツ収縮と局所時間を使えば、電磁気の法則は、あらゆる慣性系において、まったく同じ形で成立することを指摘した。いいかえれば、電磁気の法則は、相対性原理を満たしていることを発見した。
ローレンツ変換、光速度の一定性、ローレンツ収縮、局所時間、同時刻の相対性、ローレンツの相対性理論のなかには、必要なものはすべてそろっていた。しかし、ローレンツの相対性理論は、ガリレイの相対性原理と関連することなく、それとの関係をあいまいにしたまま、電磁気学だけに限定されたものであった。また、ローレンツ収縮や局所時間が、どうしておこるかの説明は納得のいくものではなかったのである。
相対性理論の形成過程におけるローレンツは、ニュートン力学の形成過程におけるケプラーと対応するのだと思う。ローレンツがつかんだ相対性理論の核心はさまざまな偶有性につつまれていたのである。
『神は老獪にして…』(アブラハム・パイス/西島和彦監訳)に、次のようにある。
大問題は、もちろん二つの基本原理の両立性の問題であった。それについてアインシュタインは、1907年の概説論文の中で、次のように言った。「驚くべきことに、最初にあげた困難[すなわち、マイケルソン‐モーリーの実験のことで、アインシュタインはこの1907年の論文の中で初めてこれに言及した]を克服するには、時間の概念を十分に正確に定めることが必要なだけであるとわかった。ローレンツによって導入され、“局所時間”と命名された補助的量が、純粋で単純な“時間”としてはっきり規定される、という洞察が必要なことのすべてであった。」
「局所時間」を「純粋で単純な“時間”」として規定することは、相対性原理を電磁気の法則だけでなく力学にも拡張することを意味している。ガリレイの相対性原理を正しいものとして前提せず、物理学のすべての法則に対して、相対性原理を要請することが求められたのである。電磁気学で成立している「相対性原理」と「光速度一定の原理」を力学にも拡張することができるのか、この姿勢がアインシュタインとローレンツを区別したのである。「相対性」と「光速度一定」の意味と価値が「局所時間」をきっかけにして、変容しはじめるのである。
ローレンツとアインシュタインの違いは、マックス・ポルンが過不足なく指摘していると思う。ボルンは1955年のベルンにおける講演でホイッテイカーの見解を批判して、次のように論じているという。(安孫子誠也「アインシュタイン相対性理論の誕生」参照)
①ローレンツ自身がアインシュタインを相対性原理の発見者だとみなしており、さらにローレンツは生涯にわたって絶対空間と絶対時間の概念を放棄しようとはしなかった。
②アインシュタインの一九〇五年論文の刺激的な特徴は、ニュートンの公認された哲学、すなわち空間と時間に関する伝統的概念に異議申し立てをした勇敢さなのである。
アインシュタインはある手紙の中で述べている。
特殊相対性理論の新しい特徴は、ローレンツ変換の振舞いがそのマクスウェル方程式との関連性を超えて、時間と空間の本性に関係していることを明らかにした点である。もう一つの新しい結果は、「ローレンツ不変性」こそは、あらゆる物理理論にとっての一般的条件だという点である。
アブラハム・パイスは、次のようにローレンツを紹介している。
私がローレンツを理解しているところでは、彼は理論物理学における指導者であり、特殊相対性理論のあらゆる物理的、数学的面を完全に把握していたが、それにもかかわらず、最愛の古典的過去にすっかり別れを告げることができたわけではなかった。この態度は自我の葛藤とは何も関係がない。そういうものは彼にとっては異質のものであった。アインシュタインとポアンカレは常に彼を賞賛し、ローレンツは常に返礼した。そしてまた彼はどこで誤ったかをはっきりさせるのをためらわなかった。「[特殊相対論の発見にあたって]私の失敗の主な原因は、変数 t だけが真の時間と考えうる量で、私の局所時間 t’は補助的数学量にすぎないとみなさねばならないという考えに、私が執着したことであった」と彼はコロンビア講義の第2版の付記に書いた。
「[特殊相対論の発見にあたって]私の失敗の主な原因は、変数 t だけが真の時間と考えうる量で、私の局所時間 t’は補助的数学量にすぎないとみなさねばならないという考えに、私が執着したことであった」。感動的な自己評価だと思う。
これに、アインシュタインの自己評価を対置してみよう。「ローレンツによって導入され、“局所時間”と命名された補助的量が、純粋で単純な“時間”としてはっきり規定される、という洞察が必要なことのすべてであった」。やはり感動的である。
ローレンツとアインシュタイン。二人の違いは、ケプラーとニュートンの違いに対応すると思う。
廣松渉は『相対性理論の哲学』のなかで、次のように述べている。「アインシュタインには、弁証法的な否定性の論理や対話性の論理が欠けていることなどを指摘するまでもなく、これは体系構成法の外面的形式に関する一面に限られる。」これは貴重な見解に思えた。廣松渉の弁証法とわたしの弁証法を対照して展開できるのではないかと思えたのである。
『相対性理論の哲学』の優れた点は、アインシュタインの「原理」とカッシーラーの「函数」を結びつけたことである。しかし、かれは「函数」をアインシュタインの2つの原理(相対性原理と光速度一定の原理)ではなく、ローレンツ変換に見た。ローレンツ変換に「函数」を見る廣松弁証法を通して、2つの原理に「函数」を見る弁証法を展望する。
「相対性理論のなかの廣松弁証法――その生成と消滅」をまとめたので、案内する。
目次は次のようである。
はじめに
1 原始函数の整型と充当 ――弁証法の体系構成法
2 廣松弁証法の生成
3 廣松弁証法の消滅
4 弁証法の消滅と生成
参考文献
アインシュタイン/内山龍雄訳『相対性理論』岩波文庫1988
マルクス/向坂逸郎訳『資本論(1)』岩波文庫 1969
廣松渉『弁証法の論理』青土社 1980
廣松渉・勝守真『相対性理論の哲学』勁草書房 1986
カッシーラー/山本義隆訳『実体概念と函数概念』みすず書房1979
金子務編『未知への旅立ち』小学館 1991
湯川監修『アインシュタイン選集』3 共立出版 1971
目次
はじめに
複合論の概略
複合のアインシュタインモデル
はじめに
これまでに、アインシュタインがソロヴィーヌへ送った手紙のなかで示した思考モデルについて、考えてきた。思考モデルにおける自己表出と指示表出の軸、悟性と理性の関係、「論理的なもの」と「経験的なもの」の違い、下向(原理の発見)と上向(構成的努力)、発見的思考(伊東俊太郎)とテマータ(G・ホルトン)の関係などである。
これらは複合論と関連しているが、複合論そのものではなく、もっと広い認識論であり、いわば複合論の背景だった。ここでは、複合論そのものを、アインシュタインが示した思考モデルを利用して、図示してみようと思う。まず、複合論を確認し、次に図を示そう。
複合論の概略
複合論は弁証法の新しい理論である。「矛盾と止揚」のヘーゲル弁証法に対して、複合論は「対話と止揚」の弁証法である。ヘーゲル弁証法は論理学・存在論・認識論にまたがる巨大なものである。これに対して、複合論は認識の領域だけに位置づく小さな道具(方法・技術)である。反対する人は多いと思われるが、わたしは認識に限定した方が弁証法(ディアレクティケー)の核心は捉えられると考えているのである。
複合論の基礎にある考え方は、ヘーゲルが「論理的なもの」に想定した悟性・否定的理性(弁証法)・肯定的理性(思弁)という三側面(三段階)を解体して、「論理的なもの」に「自己表出と指示表出」を想定していることである。また、ヘーゲルでは直列につながっている否定的理性と肯定的理性を切り離して、二つの理性の並列構造を想定していることである。
わたしが想定している「論理的なもの」とは、なにかについての認識を表現してあるものを指している。例えば、理論、命題、法則、主張、規定、見解、意見、公式などである。
複合論の特長の一つは、モデルを提示していることである。
「論理的なもの」を複素数をモデルにして表示する。例えば、A =a+bi という式で、ある特定の「論理的なもの」を表現する。実数部分が自己表出、虚数部分が指示表出である。
複合論は、複素数のかけ算をモデルとして、対立物を統一する過程を表現する。
この過程は二つの「論理的なもの」の選択から始まり、否定的理性と肯定的理性(二つの理性の同時進行が推論である)によって進展していく。
二つの「論理的なもの」の対話を表現したものが、弁証法の共時的構造(対話の四肢構造)である。
c ← bi + a → di
↑ ↓
bi ← c + di → a
中央にある bi + a と c + di は、選択された二つの「論理的なもの」である。垂直方向の矢印は推論を示している。推論によって四隅に、第三の要素が出現する。
そして、第三の要素は結合すると想定する。
c ← bi + a → di
+ ↑ ↓ +
bi ← c + di → a
右側の a + di と左側の c + bi である。これらは異なる二つの「論理的なもの」の、一方の自己表出と他方の指示表出で構成される。混成モメントである。
対立物の統一の過程は、選択・混成・統一という三段階をたどる。これが弁証法の通時的な構造である。
1(選択) 複数の「論理的なもの」の中から、対象の把握に関連がありそうな「論理的なもの」を二つ選択する段階。
2(混成) 二つの「論理的なもの」を対立させ、出現するモメントを混成する段階。
3(統一) 混成した二つの規定を統一することによって、対象に対応する一つの「論理的なもの」を確定する段階。
この三段階は、ヘーゲルの「論理的なものの三側面」に対置する過程である。ヘーゲルの弁証法は、「正反合」である。一つの「論理的なもの」の内在的否定によって進展していく。これに対して、複合の弁証法は、「正々反合」である。二つの「論理的なもの」の対話によって進展していく。記号で表示すれば、次のようになる。
1(選択) A =a+bi
A' =c+di
2(混成) A×A' =(a+bi)×(c+di)
≒(a+di)×(c+bi)
3(統一) =(ac-bd)+(ab+cd)i
=x+yi
=B
共時的な構造の中央にある bi + a と c + di は、通時的な構造の2(混成)の上部( a + bi )×( c + di )に対応している。また、共時的な構造の両側の a + di と c + bi は、2(混成)の下部( a + di )×( c + bi )に対応している。
共時的な構造の中央にある bi + a と c + di は、両側の a + di と c + bi を混成することによって役割を終えて、ここの段階で「止」まる。そして、混成モメントは次の統一の段階へと「揚」がる。この事態が、弁証法の「止揚」を表わすと考えている。
混成の段階(a+bi)×(c+di)≒(a+di)×(c+bi)において、=ではなく≒で表記しているは、この過程が論理的な過程ではなく、何らかの形で飛躍を含んでいるからである。また、混成モメント(a+di)×(c+bi)の後が、ふたたび=(等号)にもどるのは、この過程は論理的な過程だからである。
AとA' のかけ算は、(a+bi)×(c+di)=(ac-bd)+(ad+bc)iである。一方、混成モメントのかけ算は (a+di)×(c+bi) =(ac-bd)+(ab+cd)i である。前者(ac-bd)+(ad+bc)i と 後者(ac-bd)+(ab+cd)iの差が、複合(弁証法)によって創造されたものを表わしている。例えば、相対性理論に関連させていえば、前者はローレンツのローレンツ変換を表わしている。後者はアインシュタインのローレンツ変換を表わしている。
複合論は、二つの「論理的なもの」の固有の自己表出と指示表出を基点として、これまでになかった自己表出と指示表出をつくり上げ、新しい一つの「論理的なもの」が形成されていく過程を表わしているのである。
複合のアインシュタインモデル
それでは、ホルトンがテマータを示した図を基にして、複合の過程を描いていくことにしよう。
ホルトンが示した図は次のようなものであった。ここで、Eは経験、Jは飛躍、Aは公理、Sは命題を表わしている。また、θはテマータ(発見的思考)を表わしている。

アインシュタインの思考モデル
作図のポイントは、以下の5点である。
1 テマータは、J(飛躍)を方向づけるものである。複合(弁証法)はテーマ(テマータの単数)だから、1つのJ(飛躍)を描くことによって、ホルトンの図からテマータ(θ)の四角形を消去する。
2 複合の出発点は2つの「論理的なもの」(AとA')である。図のSとSの白丸を利用する。そのために、AからSとS'に向かう実線の矢印を消す。そしてSとS'をAとA'に置きかえる。
3 J(飛躍)の起点を右方向にずらし、AとA'(SとS')の中央にして、起点をB'と記入する。これは、様相性と複合論の関係を考察したときに導入したB'と同じものである。すなわち、B'はAとA'の邂逅を反映する特異点である。
4 J(飛躍)の終点、少し大きめの白丸は、Aと示されているが、これをB"に置きかえる。このB"は、ここではじめて導入するものである。混成モメントの形成を反映する特異点である。
5 到達点はBである。これはS"を利用する。実線の矢印をそのまま利用して、S"をBに置きかえる。
以上を基に作図したものが、複合のアインシュタインモデルである。

複合のアインシュタインモデル
B' は(a+bi)×(c+di)、B" は(a+di)×(c+bi)、B は(ac-bd)+(ab+cd)i と対応する。また、J(飛躍)の過程は、弁証法の共時的構造(対話の四肢構造)と対応する。すなわち、
c ← bi + a → di
↑ ↓
bi ← c + di → a
である。
複合の過程は、B' ― J ― B" ― B と表示できる。縮めれば、B' ― B" ― Bである。これが「選択―混成―統一」に対応する。B' ― J ―B" が下向(原理の発見)である。B" ― B が上向(構成的努力)である。
相対性理論はどのような複合によって形成されたのかは、別稿で展開する予定である。ここでは、これまでに示した複合の例を一つだけ確認して終わることにする。構造と過程がはっきりしているマクスウェルの複合である。
マクスウェルの弁証法において、B'(AとA' )は「アンペールの法則」(電流は、回転的な磁場を作る)と「ファラデーの法則」(磁場の変動は、回路に電場を作る)である。
B" は「マクスウェル法則」(電場の変動は、回転的な磁場を作る)と「ファラデーの法則」(磁場の変動は、回転的な電場を作る)である。
またB は「磁場のみが現れる式」(横波に対する波動方程式の形)と「電場のみが現れる式」(横波に対する波動方程式の形)である。
参考記事
「もうひとつのパスカルの原理」(『試行』№70 1991)で提起した複素過程論は、バイソシエーション(ケストラーの創造活動の理論)を、わたしなりに総括したものである。複素過程論を発展させていこうとする試みのなかで、思いがけない出来事が起こった。複素過程論が弁証法の理論と結びつくように思えてきたのである。それ以来、弁証法について考えている。
複合論は弁証法の新しい理論である。しかし、なによりも創造活動の理論である。もちろん、複合論(弁証法)はすべての創造活動を要約するものではない。創造活動の一つの領域に位置するのである。
複素過程論から複合論を切り離し、弁証法の理論として提起するさいに、重要な契機となったのは、「科学的発見の論理――創造の科学哲学的考察」(伊東俊太郎『科学と現実』中公叢書1981所収)だった。
伊東俊太郎は、そのなかで「現代の主導的な科学哲学」が、「"発見"という創造の行為を通して発展してゆく科学の最もヴィヴィトな局面を、科学認識の論理的分析の対象となりえないとして切り落としてしまった」ことに対して、疑問を述べていた。
たしかに筆者もデータから法則や理論をひき出してくる一義的な機械的な方法は存在しないことは認める。この意味でそれに従えばいつでも発見が可能となるような「発見のアルゴリズム」はどこにもない。また発見には「創造的想像力」の必要なことも認める。さらにその発見者の素質や環境といった心理的・社会的要因も重要な役割を果すことも認める。それらをすべて認めた上でなお、この発見の過程を全く不合理なもの、直観や偶然に帰せしめるより他はない分析不能なものと考える必要はないと思う。新しい仮説を提起するにはそれぞれ「理由」(ラテイオ)があり、その意味でこの過程はなお合理的(ラショナル)なものと言いうる。それゆえそれはまた必然的な形式論理の意味では論理的ではないが、仮説提起の過程がけっして心理的社会的なもののみに還元できない、それ自身合理的に分析可能な構造をもつという意味では、論理的認識論的分析の対象となるのであり、それは、科学哲学や科学方法論の領域においてもとり上げらるべき問題であると考える。これを非合理な″霊感″といったような神秘の領域にとじこめてしまうべきではないのである。
このような立場から、伊東俊太郎は「発見的思考」を提起した。その思考を、A帰納(induction)によるもの・B演繹(deduction)によるもの・C発想(abduction)によるものの三つの思考方式に分け、「C発想」のなかを、さらに1類推によるもの・2普遍化によるもの・3極限化によるもの・4システム化によるものと細分した。
| 発見的思考 | 例 | |
| A帰納 | ボイルの法則、スネルの法則 | |
| B演繹 | ニュートンの逆自乗の法則 | |
| C発想 | 1類推 | ダーウィンの自然選択説、ドゥ・ブロイの波動力学 |
| 2普遍化 | ニュートン力学、アインシュタインの相対性理論 | |
| 3極限化 | ガリレイの「慣性の法則」・「自由落下の第一法則」 | |
| 4システム化 | メンデレーエフの周期律 | |
伊東俊太郎は「普遍化」の例として、ニュートン力学とアインシュタインの相対性理論をあげていた。わたしは弁証法を「発想」の中の「普遍化」と考えればよいのではないかと思ったのである。
この「普遍化」というのは、与えられた既知の複数の理論を、ある観点から統一的に把握しうる、より一般的な理論をつくろうとすることを意味する。たとえばニュートンがガリレオによって与えられた地上の物体の運動法則と、ケプラーによって樹立された天体の運動法則とを、万有引力の観点から統一的に把握する、彼の古典力学をつくり上げたこと、またアインシュタインが、力学とマクスウェルの電磁気学を、ローレンツ変換という観点から統合する相対性理論をつくり上げたことなどが、この好例としてあげられよう。すなわち電磁気学の方はローレンツ変換を満足するが、ニュートン力学はこれを満足しないので、後者をガリレイ変換によって不変なものから、ローレンツ変換によって不変なものへと変え、両者を統合しようとしたことが、相対性理論を生み出す根本動機であった。
「発見的思考」をアインシュタインの思考図式のなかに位置づけておこうと思う。
ホルトンは「科学理論の形成に関するアインシュタインのモデル」(『アインシュタイン』岩波書店 2005 所収)のなかで、次のように述べていた。
ここで、これまで手をつけないでおいた重要な問題点を、あらためてとりあげなければならない。問題はつぎのように立てられる――-図1の図式の出発点をなすEからAへの飛躍は、論理的に不連続であり、想像力の「自由な遊び」の表現であるから、そうして、この飛躍は結果として数限りないAをつくりだすのだから(もっとも、その大多数は、やがて、理論体系の形成には何の役にも立たないとわかるだろうが)、飛躍の成功の要因として、偶然のほかに、いったい何が期待できるのであろうか? J過程における自由とは、飛躍を行なうことが許されているのであり、どんな飛躍でも勝手に行なってよいわけではない、というあたりに答があるに違いない。公理体系はやがて、アインシュタインのいうよい理論の第二の判定基準にあうかどうかをみるために、自然性とか単純性のテストにかけられるのだから、その点だけからいっても、Jを導き方向づける何かがなければならない。
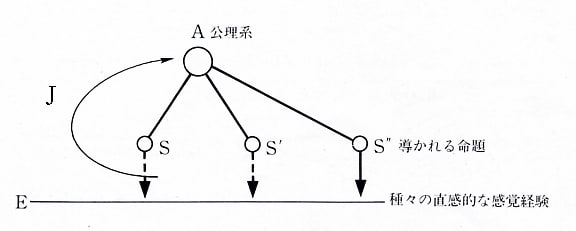 図1
図1
ホルトンは、「Jを導き方向づける何か」を「テマータ」とよんでいる。伊東の「発見的思考」は、この「テマータ」と重なると思う。
ケプラーの時代に始まり、アインシュタイン、ボーアをへて現代の最先端にいたる、数々の科学的仕事の個別研究を通じて、私が示そうとつとめてきたように、まさにこのような、正当性も虚偽性も立証できないが、まったく勝手でもない考え方の設定や使用が、たしかに存在するといえる。科学的思考の一定の段階では、存在するだけでなく、必然性さえあるのである。こういう一連の考え方を私はテマータとよんだ。
ホルトンは例を挙げている。
理論形成にあたってアインシュタインを導いたテマータとしては、つぎのようなものが認められる。形式的な(物質主義的でない)説明の優位、統一性(あるいは統一化)と宇宙論的な規模(諸法則の、経験の全領域にわたる平等な適用可能性)、論理的な倹約と必然性、対称性、単純性、因果性、完全性、連続性、それからもちろん、定値性と不変性がある。個々の場合にアインシュタインが、実験による検証が難しいとか入手不可能と思われるときでさえ、頑固にある方向の仕事を続けていった理由は、まさにこれらのテマータで説明されるのである。これはまた、テマータ的な前提条件が自分のものとは対立するような諸理論(たとえばボーア学派の量子力学)を、実験との相関はきわめてよいにもかかわらず、なぜ拒否したかをも説明する。
そして、テマータの場所を図1に示している。
こういう考え方も、EJASE過程にテマータの機能を明示するような修正をほどこすことによって、図1の図式に組み込むことができる(図7)。EからAへの飛躍にはいろいろありうるが、特定の理論家の採用した、あるいは思考過程にしみこんだテマータというフィルターを通るときに、一つか二つに濾過されてしまうのである。たとえば、アインシュタインの一九〇五年の相対論の論文の冒頭で、要請の地位にひきあげられる二つの推測も、テマータによって方向づけられている。ここでは諸法則の大規模で平等な適用可能性、不変性、論理的な倹約、形式的な説明の優位といった要求をあらかじめたてているわけである。
 図7
図7
伊東俊太郎の「発見的思考」は図のθと同じ場所にあり、J(飛躍)を方向づけていると思われる。
さて、テマータは、themata と書くようである。(「パラダイム」から科学的探究の源泉としての「テマータ」へ From "Paradigm" to "Themata" as Origins of Scientific Thought 杉山 聖一郎 1愛媛大学法文学部 参照) themataは、thema(=theme)の複数形である。thema(=theme)は、テーマ(主題・主旋律など)のことである。しかし、認識の枠組みを意味する「パラダイム」が、語形変化の一覧表に基づいていることと対照すれば、テーマは、主題というよりも、語形変化において変化しない部分、すなわち「語幹」と捉えた方が根本的だと思われる。テマータ(themata)は「語幹群」である。
「正当性も虚偽性も立証できないが、まったく勝手でもない考え方の設定や使用が、たしかに存在するといえる。科学的思考の一定の段階では、存在するだけでなく、必然性さえあるのである。こういう一連の考え方」(テマータ)と「発見的思考」は対応していると考えられる。
しかし、上に挙げられているテマータの例(硬い訳語ばかりである)は雑然としているように思われる。すくなくとも伊東俊太郎の発見的思考の分類ほど整然とはしていない。ホルトンがテマータとして挙げている例を切り捨て、「発見的思考」のA帰納・B演繹・C1類推・C2普遍化・C3極限化・C4システム化を、テマータ(「語幹」)の例としてみた方がわかりやすいのではないかと思われる。
ホルトンは「一九〇五年の相対論の論文の冒頭で、要請の地位にひきあげられる二つの推測」(相対性原理と光速度一定の原理)が、テマータ(諸法則の大規模で平等な適用可能性、不変性、論理的な倹約、形式的な説明の優位)によって方向づけられるとみている。
これに対して、わたしは、二つの推測は「弁証法」によって方向づけられると主張することになる。
アインシュタインは、理論家の仕事は2つの部分に分かれると述べていた(「プロシャ科学アカデミーにおける就任講演」1914 )。「課題の第一の部分と第二の部分」である。わたしには、「課題の第一の部分」は「下向」、「課題の第二の部分」は「上向」と対応するように思われた。
アインシュタインは「相対性理論とは?」のなかで、物理学の理論には2種類あるといっている。構成的理論と原理的理論である。
物理学の理論といっても種々な様式の理論を区別することができる。大部分の理論は構成的な様式をとっている。この種の理論は比較的簡単な基本になる理論形式から出発して、より複雑な現象の描像を構成しようとするものである。この意味で気体の運動論は力学的・熱的諸現象や拡散過程を分子の運動に帰着すること、換言すればそれらを分子運動の仮説から再構成することをねらうものである。一群の自然過程を理解することに成功したといわれる場合は、それはつねに問題の諸過程を包括する構成的な理論が見出されたことを意味するのである。しかしながら、この種の最も重要な種類の理論とともに第二の種類の理論が存在するが、私はそれを原理理論(Prinzip-Theorie)とよぶことにしたい。この種の理論は総合的方法ではなくて分析的方法を利用する。この種の理論の出発点ないしは基礎を形成するのは仮説的な構成要素ではなく、経験的に見出された自然過程の一般的性質であり、個々の過程あるいはその理論的描像が満たすべき判定条件の数学的形式を導くところの原理なのである。このような意味で熱力学は永久機関が不可能であるという一般的な経験事実から出発して解析的方法に則って個々の過程が満足すべき連関を与えようとするもののである。
構成的理論の長所は完結性・適応性および直観性であり、原理的理論の長所は論理的完全性と基礎の確実性にあるのである。
この2つの理論は、「課題の第一の部分と第二の部分」と密接に関連している。構成的理論は課題の第二の部分と、また、原理的理論は課題の第一の部分と大きく重なっている。構成的理論は課題の第二の部分と対応するといわないで、大きく重なっているというのは、構成的理論も原理的部分をもっていると思われるからである。同じように、原理的理論は課題の第一の部分と対応するといわないで、大きく重なっているというのは、原理的理論も構成的部分をもっていると思われるからである。しかし、このようなふくみを理解しておけば、課題の第一の部分と原理的理論は対応し、課題の第二の部分と構成的理論は対応するといってもいいだろう。
構成的理論とは、「仮説的な構成要素」を出発点にするものである。また、原理的理論とは「経験的に見出された自然過程の一般的性質」を出発点にするものである。
1905年のアインシュタインの論文で言えば、光量子論とブラウン運動の理論は構成的理論とみることができるだろう。それに対して、特殊相対性理論は原理的理論といえるだろう。
アインシュタインがソロヴィーヌへあてた手紙の中で示した思考モデルでいえば、構成的理論ではEJASE過程のすべてをはじめから問題にするのではなく、ASE過程だけを問題にする。出発点とするA(「仮説的な構成要素」)が存在しているからである。これに対して、原理的理論では、出発点とするA(「仮説的な構成要素」)がなく、最初のE(経験的に見出された自然過程の一般的性質)から、EJASE過程のすべてをはじめから問題にせざるをえないのである。 トーマス・クーンの表現でいえば、構成的理論は通常科学、原理的理論は革命科学といえるのではないだろうか。
アインシュタインは「自伝ノート」のなかで電磁気学の基礎の研究に対して自分自身に起こった方向転換を次のように述べている。
このような考察のおかげで、一九〇〇年を少しすぎたころ、すなわち、プランクの画期的な研究のでた直後には、すでに私には、力学と熱力学のどちらもが(限定的な場合を除いて)厳密な正確さを要求しえないものだとわかっていた。しだいに私は、既知の事実に基づいた構成的な努力によって、真の法則を見いだす可能性に絶望していった。長く、そして絶望的に努力すればするほど、ある一般的な形式を備えた原理を見つけることだけが、われわれを確実な結果に導きうるのだろうという確信が深まっていった。手本として私の前にあったのは、熱力学である。
既知の事実に基づいた構成的な努力によって、真の法則を見いだす可能性はないという絶望。ある一般的な形式を備えた原理を見つけることだけが、われわれを確実な結果に導きうるのだろうという確信。 これまでの構成的努力をやめ、はじめからやり直すこと。相対性理論が誕生する前夜のことである。
アインシュタインの「下向と上向」は、「自伝ノート」のことばを借りていえば、「原理の発見と構成的努力」と特徴づけてよいのではないかと思う。
わたしは、アインシュタインの思考図式(G・ホルトンの図示)に、下向と上向を位置づけた。(「1905年における光の粒子性と波動性について」参照)
 アインシュタインの思考図式
アインシュタインの思考図式
ここで、EJA過程(上昇する曲線)が下向である。Eは経験、Jは飛躍、Aは公理を表している。AS過程(下降する直線)が上向である。Aは公理、Sは命題を表している。
下向と上向は、マルクスのことばである。アインシュタインは、「プロシャ科学アカデミーにおける就任講演」(1914 )のなかで、「課題の第一の部分と第二の部分」と言っている。わたしには、「下向」と「課題の第一の部分」、「上向」と「課題の第二の部分」は正確に対応しているように思える。
理論家の方法としては、彼が種々の結論をそこから演繹してくる一般的前提、いわゆる原理をその基礎として用いることが当然必要になります。したがって理論家の仕事は次の二つの部分に分かれます。彼が第一にしなければならないのはこの原理を発見することであり、次には原理から出てくる種々の結論を展開しなければなりません。ここにあげた課題の第二の部分を果たすためには彼は学校において立派な準備を受けています。したがって、ある分野の、あるいは複雑に関連しあった現象に対して課題の第一の部分が一旦解決された暁には、十分な勤勉さと理解力をもってすれば成果には事欠かないでしょう。ところで課題の第一の部分、すなわち演繹に際して基礎として役に立つはずの原理を確立するということは、全く別の種類の仕事なのであります。この場合、目標に到達するのに、教えてもらえるような、組織だって応用すればよいという方法はなんら存在しません。むしろ研究者は経験的事実の厖大な複合体の中で正確な定式化を許すある種の一般的な特徴をつかむことによって、この一般的原理の本性を徐々にかぎつけなければなりません。一旦この種の定式化に成功したとなりますと、そこで種々の結果が展開されてくることになります。そしてそれが、原理が獲ちとられた経験領域をはるかに越えて、思いもかけない現象間の関連を与ることになるのがしばしばです。(『アインシュタイン選集3』所収)









