オイラーはネイピア数(自然対数の底)を導入した。

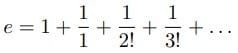
この直後の節(§123)で、オイラーは「それゆえ、双曲線対数(自然対数のこと)には、数1+ωの対数がωに等しくなるという性質が備わっている」と述べている。
任意の対数
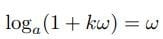
でk=1(a=e)とすれば、log(1+ω)=ωになることはわかる。しかし、ネイピア数の導入と直結している「それゆえ」がわからなかった。
次のように考えればよいことに気づいた。ネイピア数の導入

において、1/n=ωとおくと、左辺は

となる。
ここで両辺の対数(底e)をとると、
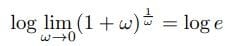

したがって、log(1+ω)=ωである。

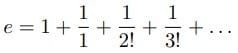
この直後の節(§123)で、オイラーは「それゆえ、双曲線対数(自然対数のこと)には、数1+ωの対数がωに等しくなるという性質が備わっている」と述べている。
任意の対数
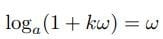
でk=1(a=e)とすれば、log(1+ω)=ωになることはわかる。しかし、ネイピア数の導入と直結している「それゆえ」がわからなかった。
次のように考えればよいことに気づいた。ネイピア数の導入

において、1/n=ωとおくと、左辺は

となる。
ここで両辺の対数(底e)をとると、
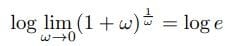

したがって、log(1+ω)=ωである。









