オイラーは指数も対数も冪から導いている(『オイラーの無限解析』7章)。これは「普通なら無限解析で扱われる」問題を、「通常レベルの代数の諸規則に基づいて」解いたことにあたる(「 」は緒言の表現)。
無限解析から代数への移行は次のようだったろう。指数関数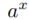 の導関数
の導関数
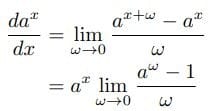
において、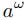 -1とωの比をkとおく。すなわち、
-1とωの比をkとおく。すなわち、
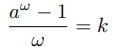
である。したがって、

これが指数関数導出の出発点となる(注)。aを底にとれば、
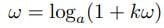
となる。こちらが対数関数の出発点となった。
kのまま展開すれば任意の指数と対数が導かれる。k=1(底a=e)とすれば自然指数と自然対数が導かれる。
緒言より(高瀬正仁訳)
オイラーはこの式から、さらに遡り、
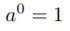
から7章を始めている。
無限解析から代数への移行は次のようだったろう。指数関数
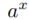 の導関数
の導関数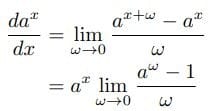
において、
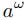 -1とωの比をkとおく。すなわち、
-1とωの比をkとおく。すなわち、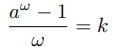
である。したがって、

これが指数関数導出の出発点となる(注)。aを底にとれば、
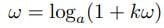
となる。こちらが対数関数の出発点となった。
kのまま展開すれば任意の指数と対数が導かれる。k=1(底a=e)とすれば自然指数と自然対数が導かれる。
緒言より(高瀬正仁訳)
対数や円弧は双曲線や円の面積を通じて表示されるのであるから、超越的な量であり、無限解析で取り扱われるのが普通の姿である。しかし私は幕から出発して指数量へと歩を進めた。指数量というのは、その幕指数が変化量である幕にほかならないが、これを逆転することにより、きわめて自然で、しかも豊饒な対数の観念が手に入ったのである。このような道を歩むと、対数というもののめざましい効用がおのずと明るみに出されるが、そればかりではない。普通、対数を表示するのに使われる習慣が確立されているあらゆる無限級数もまた、この道筋の中から取り出されてくるのである。それに、対数表を作成する方法も、この道筋をたどることによりごく簡単に明らかになる。(注)
オイラーはこの式から、さらに遡り、
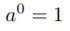
から7章を始めている。









