『新天文学』の本文や訳注などを読むかぎり、「視覚的均差」は離心円上で位置づけるものであることは疑いようもない。しかし、山本義隆や酒井邦嘉はそれぞれの本(『世界の見方の転換3』、『高校数学でわかるアインシュタイン』)で楕円上に位置づけている。
2人の展開を確認しておこう。酒井邦嘉について疑問に思っているのは、次の図と次の式である。
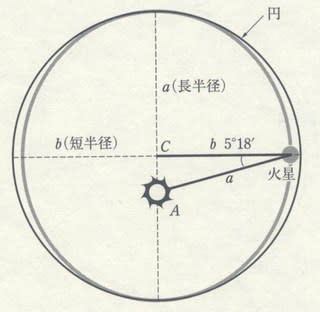
a/b=1.00429=1/cos(5°18′)
山本義隆については、次の図と次の説明である。

「さらなる新しい局面への突破口は、ここで火星-太陽間の距離が、先に述べた「直径距離」で与えられることに偶然気づいたことにある。そのことをケプラーは、離心アノーマリーが90度になり火星軌道が円からもっとも外れたときの三日月の幅(図のEF間の距離)が離心円の半径a=BF(BEの誤植 引用者注)の0.00429倍であること、そのとき∠BFAが5度18分で、そのセカント(余弦の逆数つまり1/cos5°18′)が1.00429であることからひらめいたと証言している。つまりFB=(1-0.00429)aにたいして
このように2人とも視覚的均差5°18´を楕円上に位置づけているのである。ここではケプラーを引用することなく、正割1.00429だけを目印に視覚的均差5°18´はどこの角度かを判断してもらいたいと思う。
まず、正割について確認しておこう。直角三角形ABC(∠Cが直角)において、AB(斜辺) と BC(底辺) の長さの比(BC/AB)は余弦(コサイン)cosBだが、その逆数(AB/BC)が正割(セカント)secB である。
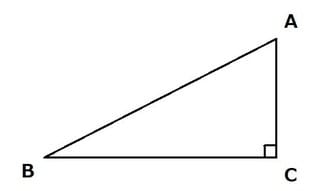
secB=1/ cosB=AB/BC
さて、ここで単純な図を提示してみよう。
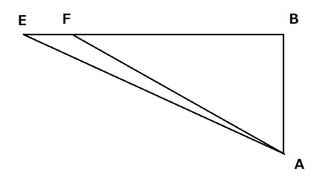
Eは離心円上の点、Fは楕円上の点、Bは離心円の中心、Aは太陽である。上の2つの図の中心部分である。上2つの図には太陽Aと離心円上の点Eを結ぶ線はないが、ケプラーの図ではEAは結ばれている。
ここには、2つの直角三角形がある。直角三角形FBAと直角三角形EBAである。実は、この図のすべての線分は長さが決まっている。それを取り出してみよう。
離心円の半径EBは1、離心距離BAは0.09265、切り取る三日月の幅EFは0.00429である。これをもとに、直角三角形に着目し三平方の定理を使って、FA、EAを求めることができる。
直角三角形FBAに着目して、
FA2=(1-0.00429)2+0.092652より、
FA=1.00001≒1
直角三角形EBAに着目して、
EA2=12+0.092652より、
EA=1.00428≒1.00429
まとめると、FA=1、EA=1.00429である。また、FB=(1-0.00429)=0.99571である。
山本義隆も酒井邦嘉も直角三角形FBAにおいて、∠BFAを5°18′と考えている。正割はFA/FB=1/0.99571になる。この計算は難しいが、これを1.00429と想定している。実際計算してみると、1.00431で近似値を示すが、1/0.99571に「新しい光」を見たとはとても思えない。
それよりも、直角三角形EBAにおいて、∠BEAに5°18′をみて、正割EA/EB=1.00429/1を1.00429と考える方が自然ではないだろうか。
実際、ケプラーが最大の視覚的均差5°18′の正割1.00429を見ていた直角三角形は△EBAであって△FBAではなかった。最大の視覚的均差5°18′は∠BEA(離心円上)であって、∠BFA(楕円上)ではなかったのである。
ケプラーは「平均的な長さを取る所で正割の代りに半径を用いると観測結果のとおりとなる」と述べた。正割EA(1.00429)の代わりに半径EB(1)を用いると観測結果FA(1)になると気づいたのである。ケプラーの発見は「円から楕円へ」と特徴づけられる。その最もコンパクトな表現がここにある。最大の視覚的均差5°18′は離心円上にあったのである。
山本義隆も酒井邦嘉もケプラーの発見の核心を捉えていないのである。
2人の展開を確認しておこう。酒井邦嘉について疑問に思っているのは、次の図と次の式である。

a/b=1.00429=1/cos(5°18′)
山本義隆については、次の図と次の説明である。

「さらなる新しい局面への突破口は、ここで火星-太陽間の距離が、先に述べた「直径距離」で与えられることに偶然気づいたことにある。そのことをケプラーは、離心アノーマリーが90度になり火星軌道が円からもっとも外れたときの三日月の幅(図のEF間の距離)が離心円の半径a=BF(BEの誤植 引用者注)の0.00429倍であること、そのとき∠BFAが5度18分で、そのセカント(余弦の逆数つまり1/cos5°18′)が1.00429であることからひらめいたと証言している。つまりFB=(1-0.00429)aにたいして
FA=FBsec(5°18′)=(1-0.00429) (1+0.00429)a≒a=EBに気づき、この「新しい光に眠りから覚まされた」のである。」
このように2人とも視覚的均差5°18´を楕円上に位置づけているのである。ここではケプラーを引用することなく、正割1.00429だけを目印に視覚的均差5°18´はどこの角度かを判断してもらいたいと思う。
まず、正割について確認しておこう。直角三角形ABC(∠Cが直角)において、AB(斜辺) と BC(底辺) の長さの比(BC/AB)は余弦(コサイン)cosBだが、その逆数(AB/BC)が正割(セカント)secB である。

secB=1/ cosB=AB/BC
さて、ここで単純な図を提示してみよう。

Eは離心円上の点、Fは楕円上の点、Bは離心円の中心、Aは太陽である。上の2つの図の中心部分である。上2つの図には太陽Aと離心円上の点Eを結ぶ線はないが、ケプラーの図ではEAは結ばれている。
ここには、2つの直角三角形がある。直角三角形FBAと直角三角形EBAである。実は、この図のすべての線分は長さが決まっている。それを取り出してみよう。
離心円の半径EBは1、離心距離BAは0.09265、切り取る三日月の幅EFは0.00429である。これをもとに、直角三角形に着目し三平方の定理を使って、FA、EAを求めることができる。
直角三角形FBAに着目して、
FA2=(1-0.00429)2+0.092652より、
FA=1.00001≒1
直角三角形EBAに着目して、
EA2=12+0.092652より、
EA=1.00428≒1.00429
まとめると、FA=1、EA=1.00429である。また、FB=(1-0.00429)=0.99571である。
山本義隆も酒井邦嘉も直角三角形FBAにおいて、∠BFAを5°18′と考えている。正割はFA/FB=1/0.99571になる。この計算は難しいが、これを1.00429と想定している。実際計算してみると、1.00431で近似値を示すが、1/0.99571に「新しい光」を見たとはとても思えない。
それよりも、直角三角形EBAにおいて、∠BEAに5°18′をみて、正割EA/EB=1.00429/1を1.00429と考える方が自然ではないだろうか。
実際、ケプラーが最大の視覚的均差5°18′の正割1.00429を見ていた直角三角形は△EBAであって△FBAではなかった。最大の視覚的均差5°18′は∠BEA(離心円上)であって、∠BFA(楕円上)ではなかったのである。
ケプラーは「平均的な長さを取る所で正割の代りに半径を用いると観測結果のとおりとなる」と述べた。正割EA(1.00429)の代わりに半径EB(1)を用いると観測結果FA(1)になると気づいたのである。ケプラーの発見は「円から楕円へ」と特徴づけられる。その最もコンパクトな表現がここにある。最大の視覚的均差5°18′は離心円上にあったのである。
山本義隆も酒井邦嘉もケプラーの発見の核心を捉えていないのである。












