「kは底aの自然対数に等しい1」では、底aと底eの対数の級数表示の比較からk=log aになることを見た。こんどは、はじめの設定

から、k=log aになることを見ておこう。
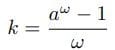
ここで、ω>0、 >1である。
>1である。
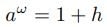 (1)
(1)
とおくと、 →0のとき、
→0のとき、 →1である。したがって、h→0である。
→1である。したがって、h→0である。
(1)式で両辺の対数(底a)をとると、

である。また、 -1=hである。
-1=hである。
したがって、
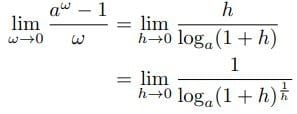 (2)
(2)
である。ここで

だから、(2)式は
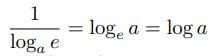
となる。
したがって、k=log aである。

から、k=log aになることを見ておこう。
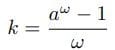
ここで、ω>0、
 >1である。
>1である。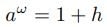 (1)
(1)とおくと、
 →0のとき、
→0のとき、 →1である。したがって、h→0である。
→1である。したがって、h→0である。(1)式で両辺の対数(底a)をとると、

である。また、
 -1=hである。
-1=hである。したがって、
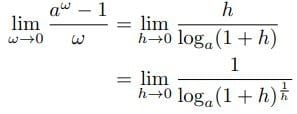 (2)
(2)である。ここで

だから、(2)式は
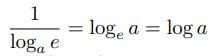
となる。
したがって、k=log aである。









